2017-2018学年人教B版必修二 2.1平面直角坐标系中的基本公式 课件(24张)
文档属性
| 名称 | 2017-2018学年人教B版必修二 2.1平面直角坐标系中的基本公式 课件(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 433.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-24 13:57:40 | ||
图片预览








文档简介
课件24张PPT。高一必修二
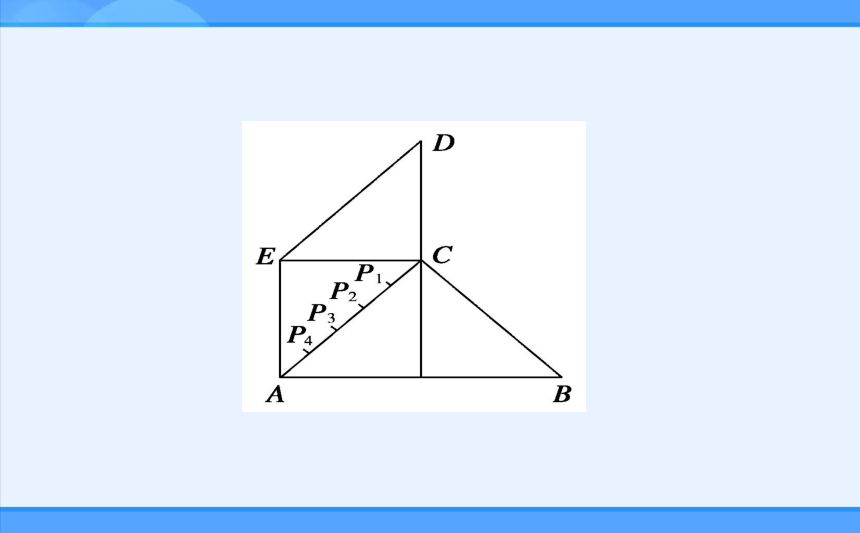
2.1 平面直角坐标系中的基本公式某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,你能判断出转播台应建在何处吗?平面直角坐标系中的基本公式
1.平面上任意两点P1(x1,y1)、P2(x2,y2)之间的
距离d(P1,P2)=|P1P2|=__________自学导引(2a-x0,2b-y0) 例1.平行四边形ABCD三个顶点坐标分别为A(2,3)、B(4,0)、D(5,3),求顶点C的坐标.
[分析] 运用中点坐标公式先求出?ABCD两对角线交点M的坐标,再求顶点C的坐标.题型一 中点坐标公式
[点评] 若给出平行四边形ABCD四点中三个A、B、C,则D点是惟一的,如果该题不指出哪三个点,求第四个点坐标,则第四个点坐标不惟一.【变式1】已知点A关于点B(2,1)的对称点为C(-4,3),C关于D的对称点为E(-6,-3),求A、D的坐标及AD中点坐标.题型二 两点间距离公式已知平行四边形三个顶点的坐标分别为(1,1)、(2,-1)、(-1,-3),则第四个顶点的坐标为________.
[错解] (-2,-1)
[辨析] 由于在解题时只考虑了以(1,1)和(-1,-3)为一条对角线的两端点时的情况,故导致错误.
易错疑难辨析
[正解] (4,3)或(-2,-1)或(0,-5) ①当(1,1)与(2,-1)为一条对角线的两端点时,第四个顶点的坐标为(4,3);②当(1,1)与(-1,-3)为一条对角线的两端点时,第四个顶点的坐标为(-2,-1);③当(2,-1)与(-1,-3)为一条对角线的两端点时,第四个顶点的坐标为(0,-5).[解析] 如图所示,以Rt△ABC为直角边AB,AC所在直线为坐标轴,建立直角坐标系,设B,C两点的坐标分别为(b,0),(0,c).
[点评] 坐标法解(证)题的关键是建立平面直角坐标系,建系的原则是将尽量多的点放在坐标轴上,以便用较少的量设出点的坐标.当题目中有直角时,通常取直角边所在的直线为坐标轴.小结:1. 面直角坐标系中的基本公式:平两点间距离公 式和中点坐标公式
2. 公式的灵活应用。作业布置习题:A组2,B组3祝同学们学习进步!
2.1 平面直角坐标系中的基本公式某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,你能判断出转播台应建在何处吗?平面直角坐标系中的基本公式
1.平面上任意两点P1(x1,y1)、P2(x2,y2)之间的
距离d(P1,P2)=|P1P2|=__________自学导引(2a-x0,2b-y0) 例1.平行四边形ABCD三个顶点坐标分别为A(2,3)、B(4,0)、D(5,3),求顶点C的坐标.
[分析] 运用中点坐标公式先求出?ABCD两对角线交点M的坐标,再求顶点C的坐标.题型一 中点坐标公式
[点评] 若给出平行四边形ABCD四点中三个A、B、C,则D点是惟一的,如果该题不指出哪三个点,求第四个点坐标,则第四个点坐标不惟一.【变式1】已知点A关于点B(2,1)的对称点为C(-4,3),C关于D的对称点为E(-6,-3),求A、D的坐标及AD中点坐标.题型二 两点间距离公式已知平行四边形三个顶点的坐标分别为(1,1)、(2,-1)、(-1,-3),则第四个顶点的坐标为________.
[错解] (-2,-1)
[辨析] 由于在解题时只考虑了以(1,1)和(-1,-3)为一条对角线的两端点时的情况,故导致错误.
易错疑难辨析
[正解] (4,3)或(-2,-1)或(0,-5) ①当(1,1)与(2,-1)为一条对角线的两端点时,第四个顶点的坐标为(4,3);②当(1,1)与(-1,-3)为一条对角线的两端点时,第四个顶点的坐标为(-2,-1);③当(2,-1)与(-1,-3)为一条对角线的两端点时,第四个顶点的坐标为(0,-5).[解析] 如图所示,以Rt△ABC为直角边AB,AC所在直线为坐标轴,建立直角坐标系,设B,C两点的坐标分别为(b,0),(0,c).
[点评] 坐标法解(证)题的关键是建立平面直角坐标系,建系的原则是将尽量多的点放在坐标轴上,以便用较少的量设出点的坐标.当题目中有直角时,通常取直角边所在的直线为坐标轴.小结:1. 面直角坐标系中的基本公式:平两点间距离公 式和中点坐标公式
2. 公式的灵活应用。作业布置习题:A组2,B组3祝同学们学习进步!
