湖南省衡阳市祁东县第二中学2016-2017学年高一下学期火箭班选拔考试数学试卷 Word版含答案
文档属性
| 名称 | 湖南省衡阳市祁东县第二中学2016-2017学年高一下学期火箭班选拔考试数学试卷 Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 443.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-10-26 00:00:00 | ||
图片预览




文档简介
祁东二中2017年高一选拔考试试题
数
学
时量120分钟,
分值150分,
考生务必将答案涂写在答题卡上,答在试卷上的无效。
一、选择题:.(
共12小题,每小题5分,共60分)
1.设集合,.若,则(
)
A.
B.
C.
D.
2.
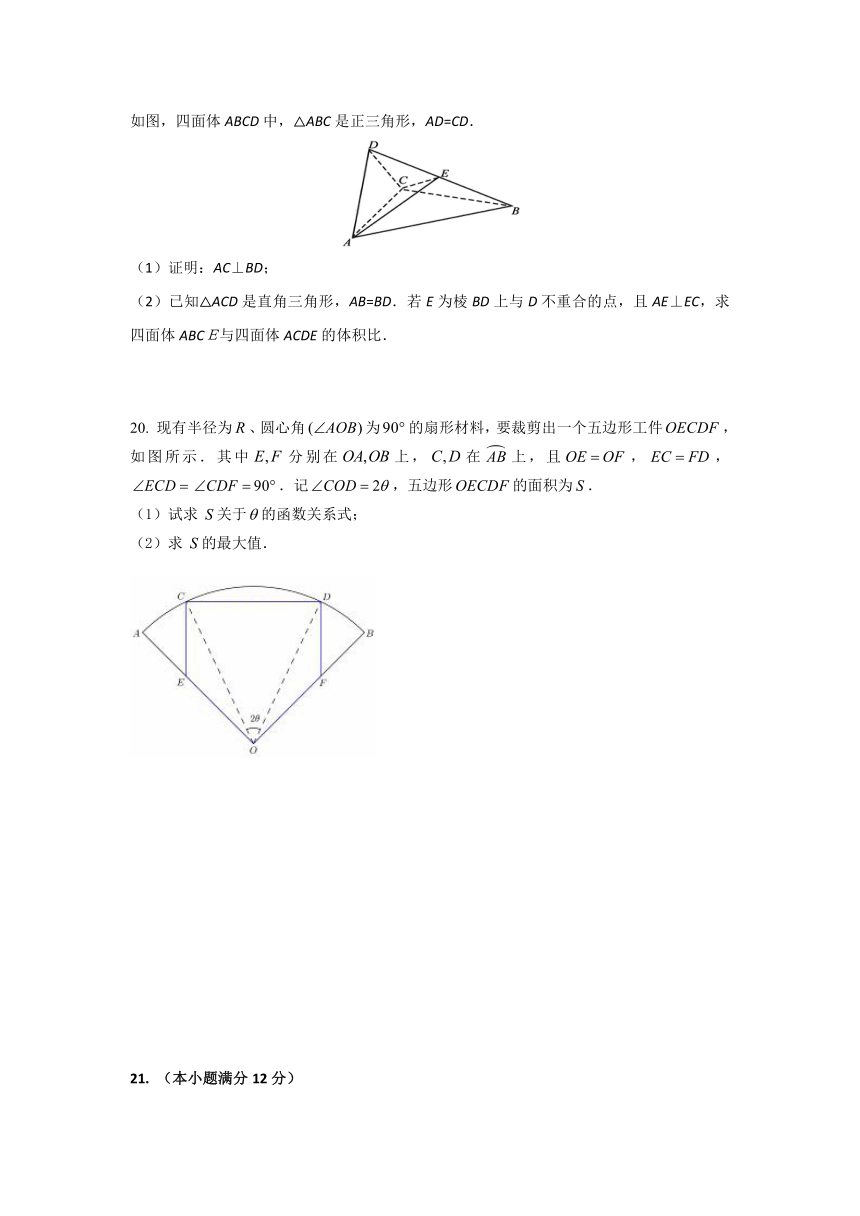
某三棱锥的三视图如图所示,则该三棱锥的体积为
(A)60
(B)30
(C)20
(D)10
3.阅读右面的程序框图,运行相应的程序,若输入的值为24,则输出的值为
(A)0
(B)1(C)2(D)3
4.甲、乙、丙、丁四位同学一起去向老师询问数学竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则
A.乙可以知道两人的成绩
B.丁可能知道两人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩
5.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A
B
C
D
6.
已知函数则的单调递增区间。
A.
B.
C..
D.
7.设函数,,其中,.若,,且的最小正周期大于,则
(A),
(B),
(C),
(D),
8.
已知奇函数在R上是增函数,.若,,,则a,b,c的大小关系为
(A)
(B)
(C)
(D)
9.
已知边长为1的正三角形的中心为O,
过O的直线与边AB,AC分别交于点M,N两点,则的取值范围为(
)
A.[15,18]
B.
[12,16]
C.
[9,18]
D.
[10,18]
10.
旅行社为去广西桂林的某旅游团包飞机去旅游,其中旅行社的包机费为10000元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在20或20以下,飞机票每人收费800元;若旅游团的人数多于20,则实行优惠方案,每多一人,机票费每张减少10元,但旅游团的人数最多为75,则该旅行社可获得利润的最大值为(
)
A.12000元
B.12500元
C.15000元
D.20000元
11.在平面直角坐标系xOy中,已知圆C:x2+(y-3)2=2,点A是x轴上的一个动点,AP,AQ分别切圆C于P,Q两点,则线段PQ长的取值范围是
A,
C.
D.
12.如图,在同一个平面内,向量,,,的模分别为1,1,,与的夹角为,且tan=7,与的夹角为45°。若=m+n(m,nR),则m+n=
A.1
B.2
C.3
D.4
二.
填空题:本大题共4小题,每小题5分,共20分.
13.
某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表如下:
气温(℃)
18
13
10
-1
用电量(度)
24
34
38
64
由表中数据得线性回归方程=x+中的=-2,预测当气温为-4
℃时,用电量可能为__________度.
14.
在区间[0,π]上随机取一个实数x,使得sin
x∈的概率为________.
15.
已知函数在区间(其中)上单调递增,则实数的取值范围是
16.
设函数则满足的x的取值范围是_____
三.
解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分10分)的内角的对边分别为
,已知.(1)求
(2)若
,
面积为2,求
18.某高校在2017年的自主招生考试成绩中随机抽取100名中学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示:
组号
分组
频数
频率
第1组
[160,165)
5
0.050
第2组
[165,170)
①
0.350
第3组
[170,175)
30
②
第4组
[175,180)
20
0.200
第5组
[180,185]
10
0.100
合计
100
1.00
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图.
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试.
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率.
19.(本小题满分12分)
如图,四面体ABCD中,△ABC是正三角形,AD=CD.
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
20.
现有半径为、圆心角为的扇形材料,要裁剪出一个五边形工件,如图所示.其中分别在上,在上,且,,.记,五边形的面积为.
(1)试求关于的函数关系式;
(2)求的最大值.
21.
(本小题满分12分)
已知,函数.(1)若,求的单调递增区间;
(2)函数在上的值域为,求,需要满足的条件.
22.(12分)
如果函数y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”;
(1)判断函数y=sinx是否具有“P(a)性质”,若具有“P(a)性质”,试写出所有a的值;若不具有“P(a)性质”,请说明理由;
(2)已知y=f(x)具有“P(0)性质”,当x≤0时,f(x)=(x+t)2,t∈R,求y=f(x)在上的最大值;
(3)设函数y=g(x)具有“P(±1)性质”,且当﹣≤x≤时,g(x)=|x|,求:当x∈R时,函数g(x)的解析式,若y=g(x)与y=mx(m∈R)交点个数为1001个,求m的值.
祁东二中2017年高一选拔考试参考答案
数
学
时量120分钟,
分值150分,
命题人
谭
扬
答卷前,考生务必将自己的姓名、考号填写在答题卷上,并在规定位置粘贴考试用条形码。答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
祝各位同学考试顺利!
一、选择题:.(
共12小题,每小题5分,共60分)
CDCDD
B
A
CAC
BC
二.
填空题:本大题共4小题,每小题5分,共20分.
13.
68
14.
.
15.
16.
(-,
)
三.
解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分10分)
(1)由题设及,故
上式两边平方,整理得
解得
(2)由,故
又
由余弦定理及得
所以b=2
18.
(1)①由题可知,第2组的频数为0.35×100=35人,②第3组的频率为=0.300,
频率分布直方图如图所示,
(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生进入第二轮面试,每组抽取的人数分别为:
第3组:×6=3人,
第4组:×6=2人,
第5组:×6=1人,
所以第3、4、5组分别抽取3人、2人、1人进入第二轮面试.
(3)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,
则从这六位同学中抽取两位同学有
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共15种,
其中第4组的2位同学B1,B2中至少有一位同学入选的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C1),(B2,C1),共’有9种,所以第4组至少有一名学生被考官A面试的概率为=.
19.解:
(1)取AC的中点O连结DO,BO.
因为AD=CD,所以AC⊥DO.
又由于△ABC是正三角形,所以AC⊥BO.
从而AC⊥平面DOB,故AC⊥BD.
(2)连结EO.
由(1)及题设知∠ADC=90°,所以DO=AO.
在Rt△AOB中,.
又AB=BD,所以
,故∠DOB=90°.
由题设知△AEC为直角三角形,所以.
又△ABC是正三角形,且AB=BD,所以.
故E为BD的中点,从而E到平面ABC的距离为D到平面ABC的距离的,四面体ABCE的体积为四面体ABCD的体积的,即四面体ABCE与四面体ACDE的体积之比为1:1.
20.
解:(1)设是中点,连,由,可知,,
,,又,,,可得△≌△,
故,可知,
…………2分
又,,所以,故
,在△中,有,
可得
………4分
所以
………6分
(2)
……………8分
(其中)
……………………10分
当,即时,取最大值1.
又,所以的最大值为.
……………12分
21.
(本小题满分12分)
【解析】(1)因为,,如图.所以的单调递增区间为,.
(2)因为在上的值域为,所以,即,
(i)当时,,所以时,,又,所以,得,此时,而,所以得,所以
(ii)当时,,所以,①当时,,所以,得,;②当时,,所以,所以,所以或,不成立.由(i)、(ii)可知或
(22)(本小题满分12分)
22.(1)由sin(x+a)=sin(﹣x)得sin(x+a)=﹣sinx,
根据诱导公式得a=2kπ+π(k∈Z).
∴y=sinx具有“P(a)性质”,其中a=2kπ+π(k∈Z).
(2)∵y=f(x)具有“P(0)性质”,
∴f(x)=f(﹣x).
设x≥0,则﹣x≤0,∴f(x)=f(﹣x)=(﹣x+t)2=(x﹣t)2
∴f(x)=
当t≤0时,∵y=f(x)在递增,
∴x=1时ymax=(1﹣t)2,
当0<t<时,y=f(x)在上递减,在上递增,且f(0)=t2<f(1)=(1﹣t)2,
∴x=1时ymax=(1﹣t)2,
当t≥时,
∵y=f(x)在上递减,在上递增,且f(0)=m2≥f(1)=(1﹣m)2,
∴x=0时,ymax=t2,
综上所述:当t<时,ymax=f(1)=(1﹣t)2,
当t≥ymax=f(0)=t2,
(3)∵y=g(x)具有“P(±1)性质”,
∴g(1+x)=g(﹣x),g(﹣1+x)=g(﹣x),
∴g(x+2)=g(1+1+x)=g(﹣1﹣x)=g(x),从而得到y=g(x)是以2为周期的函数.
又≤x≤设,则﹣≤x﹣1≤,
g(x)=g(x﹣2)=g(﹣1+x﹣1)=g(﹣x+1)=|﹣x+1|=|x﹣1|=g(x﹣1).
再设n﹣≤x≤n+(n∈z),
当n=2k(k∈z),则2k﹣≤x≤2k+,则﹣≤x﹣2k≤,
g(x)=g(x﹣2k)=|x﹣2k|=|x﹣n|;
当n=2k+1(k∈z),则2k+1﹣≤x≤2k+1+,则≤x﹣2k≤
g(x)=g(x﹣2k)=|x﹣2k﹣1|=|x﹣n|;
∴g(x)=
∴对于n﹣≤x≤n+,(n∈z),都有g(x)=|x﹣n|,而n+1﹣<x+1<n+1+,
∴g(x+1)=|(x+1)﹣(n+1)|=|x﹣n|=g(x),
∴y=g(x)是周期为1的函数.
①当m>0时,要使y=mx与y=g(x)有1001个交点,只要y=mx与y=g(x)在有一个交点.
∴y=mx过(,),从而得m=
②当m<0时,同理可得m=﹣
③当m=0时,不合题意.
综上所述m=±
数
学
时量120分钟,
分值150分,
考生务必将答案涂写在答题卡上,答在试卷上的无效。
一、选择题:.(
共12小题,每小题5分,共60分)
1.设集合,.若,则(
)
A.
B.
C.
D.
2.
某三棱锥的三视图如图所示,则该三棱锥的体积为
(A)60
(B)30
(C)20
(D)10
3.阅读右面的程序框图,运行相应的程序,若输入的值为24,则输出的值为
(A)0
(B)1(C)2(D)3
4.甲、乙、丙、丁四位同学一起去向老师询问数学竞赛的成绩,老师说,你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,根据以上信息,则
A.乙可以知道两人的成绩
B.丁可能知道两人的成绩
C.乙、丁可以知道对方的成绩
D.乙、丁可以知道自己的成绩
5.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A
B
C
D
6.
已知函数则的单调递增区间。
A.
B.
C..
D.
7.设函数,,其中,.若,,且的最小正周期大于,则
(A),
(B),
(C),
(D),
8.
已知奇函数在R上是增函数,.若,,,则a,b,c的大小关系为
(A)
(B)
(C)
(D)
9.
已知边长为1的正三角形的中心为O,
过O的直线与边AB,AC分别交于点M,N两点,则的取值范围为(
)
A.[15,18]
B.
[12,16]
C.
[9,18]
D.
[10,18]
10.
旅行社为去广西桂林的某旅游团包飞机去旅游,其中旅行社的包机费为10000元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在20或20以下,飞机票每人收费800元;若旅游团的人数多于20,则实行优惠方案,每多一人,机票费每张减少10元,但旅游团的人数最多为75,则该旅行社可获得利润的最大值为(
)
A.12000元
B.12500元
C.15000元
D.20000元
11.在平面直角坐标系xOy中,已知圆C:x2+(y-3)2=2,点A是x轴上的一个动点,AP,AQ分别切圆C于P,Q两点,则线段PQ长的取值范围是
A,
C.
D.
12.如图,在同一个平面内,向量,,,的模分别为1,1,,与的夹角为,且tan=7,与的夹角为45°。若=m+n(m,nR),则m+n=
A.1
B.2
C.3
D.4
二.
填空题:本大题共4小题,每小题5分,共20分.
13.
某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表如下:
气温(℃)
18
13
10
-1
用电量(度)
24
34
38
64
由表中数据得线性回归方程=x+中的=-2,预测当气温为-4
℃时,用电量可能为__________度.
14.
在区间[0,π]上随机取一个实数x,使得sin
x∈的概率为________.
15.
已知函数在区间(其中)上单调递增,则实数的取值范围是
16.
设函数则满足的x的取值范围是_____
三.
解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分10分)的内角的对边分别为
,已知.(1)求
(2)若
,
面积为2,求
18.某高校在2017年的自主招生考试成绩中随机抽取100名中学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示:
组号
分组
频数
频率
第1组
[160,165)
5
0.050
第2组
[165,170)
①
0.350
第3组
[170,175)
30
②
第4组
[175,180)
20
0.200
第5组
[180,185]
10
0.100
合计
100
1.00
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图.
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试.
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率.
19.(本小题满分12分)
如图,四面体ABCD中,△ABC是正三角形,AD=CD.
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
20.
现有半径为、圆心角为的扇形材料,要裁剪出一个五边形工件,如图所示.其中分别在上,在上,且,,.记,五边形的面积为.
(1)试求关于的函数关系式;
(2)求的最大值.
21.
(本小题满分12分)
已知,函数.(1)若,求的单调递增区间;
(2)函数在上的值域为,求,需要满足的条件.
22.(12分)
如果函数y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”;
(1)判断函数y=sinx是否具有“P(a)性质”,若具有“P(a)性质”,试写出所有a的值;若不具有“P(a)性质”,请说明理由;
(2)已知y=f(x)具有“P(0)性质”,当x≤0时,f(x)=(x+t)2,t∈R,求y=f(x)在上的最大值;
(3)设函数y=g(x)具有“P(±1)性质”,且当﹣≤x≤时,g(x)=|x|,求:当x∈R时,函数g(x)的解析式,若y=g(x)与y=mx(m∈R)交点个数为1001个,求m的值.
祁东二中2017年高一选拔考试参考答案
数
学
时量120分钟,
分值150分,
命题人
谭
扬
答卷前,考生务必将自己的姓名、考号填写在答题卷上,并在规定位置粘贴考试用条形码。答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
祝各位同学考试顺利!
一、选择题:.(
共12小题,每小题5分,共60分)
CDCDD
B
A
CAC
BC
二.
填空题:本大题共4小题,每小题5分,共20分.
13.
68
14.
.
15.
16.
(-,
)
三.
解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分10分)
(1)由题设及,故
上式两边平方,整理得
解得
(2)由,故
又
由余弦定理及得
所以b=2
18.
(1)①由题可知,第2组的频数为0.35×100=35人,②第3组的频率为=0.300,
频率分布直方图如图所示,
(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生进入第二轮面试,每组抽取的人数分别为:
第3组:×6=3人,
第4组:×6=2人,
第5组:×6=1人,
所以第3、4、5组分别抽取3人、2人、1人进入第二轮面试.
(3)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,
则从这六位同学中抽取两位同学有
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共15种,
其中第4组的2位同学B1,B2中至少有一位同学入选的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C1),(B2,C1),共’有9种,所以第4组至少有一名学生被考官A面试的概率为=.
19.解:
(1)取AC的中点O连结DO,BO.
因为AD=CD,所以AC⊥DO.
又由于△ABC是正三角形,所以AC⊥BO.
从而AC⊥平面DOB,故AC⊥BD.
(2)连结EO.
由(1)及题设知∠ADC=90°,所以DO=AO.
在Rt△AOB中,.
又AB=BD,所以
,故∠DOB=90°.
由题设知△AEC为直角三角形,所以.
又△ABC是正三角形,且AB=BD,所以.
故E为BD的中点,从而E到平面ABC的距离为D到平面ABC的距离的,四面体ABCE的体积为四面体ABCD的体积的,即四面体ABCE与四面体ACDE的体积之比为1:1.
20.
解:(1)设是中点,连,由,可知,,
,,又,,,可得△≌△,
故,可知,
…………2分
又,,所以,故
,在△中,有,
可得
………4分
所以
………6分
(2)
……………8分
(其中)
……………………10分
当,即时,取最大值1.
又,所以的最大值为.
……………12分
21.
(本小题满分12分)
【解析】(1)因为,,如图.所以的单调递增区间为,.
(2)因为在上的值域为,所以,即,
(i)当时,,所以时,,又,所以,得,此时,而,所以得,所以
(ii)当时,,所以,①当时,,所以,得,;②当时,,所以,所以,所以或,不成立.由(i)、(ii)可知或
(22)(本小题满分12分)
22.(1)由sin(x+a)=sin(﹣x)得sin(x+a)=﹣sinx,
根据诱导公式得a=2kπ+π(k∈Z).
∴y=sinx具有“P(a)性质”,其中a=2kπ+π(k∈Z).
(2)∵y=f(x)具有“P(0)性质”,
∴f(x)=f(﹣x).
设x≥0,则﹣x≤0,∴f(x)=f(﹣x)=(﹣x+t)2=(x﹣t)2
∴f(x)=
当t≤0时,∵y=f(x)在递增,
∴x=1时ymax=(1﹣t)2,
当0<t<时,y=f(x)在上递减,在上递增,且f(0)=t2<f(1)=(1﹣t)2,
∴x=1时ymax=(1﹣t)2,
当t≥时,
∵y=f(x)在上递减,在上递增,且f(0)=m2≥f(1)=(1﹣m)2,
∴x=0时,ymax=t2,
综上所述:当t<时,ymax=f(1)=(1﹣t)2,
当t≥ymax=f(0)=t2,
(3)∵y=g(x)具有“P(±1)性质”,
∴g(1+x)=g(﹣x),g(﹣1+x)=g(﹣x),
∴g(x+2)=g(1+1+x)=g(﹣1﹣x)=g(x),从而得到y=g(x)是以2为周期的函数.
又≤x≤设,则﹣≤x﹣1≤,
g(x)=g(x﹣2)=g(﹣1+x﹣1)=g(﹣x+1)=|﹣x+1|=|x﹣1|=g(x﹣1).
再设n﹣≤x≤n+(n∈z),
当n=2k(k∈z),则2k﹣≤x≤2k+,则﹣≤x﹣2k≤,
g(x)=g(x﹣2k)=|x﹣2k|=|x﹣n|;
当n=2k+1(k∈z),则2k+1﹣≤x≤2k+1+,则≤x﹣2k≤
g(x)=g(x﹣2k)=|x﹣2k﹣1|=|x﹣n|;
∴g(x)=
∴对于n﹣≤x≤n+,(n∈z),都有g(x)=|x﹣n|,而n+1﹣<x+1<n+1+,
∴g(x+1)=|(x+1)﹣(n+1)|=|x﹣n|=g(x),
∴y=g(x)是周期为1的函数.
①当m>0时,要使y=mx与y=g(x)有1001个交点,只要y=mx与y=g(x)在有一个交点.
∴y=mx过(,),从而得m=
②当m<0时,同理可得m=﹣
③当m=0时,不合题意.
综上所述m=±
同课章节目录
