24.1.4圆周角(第1课时) 课件

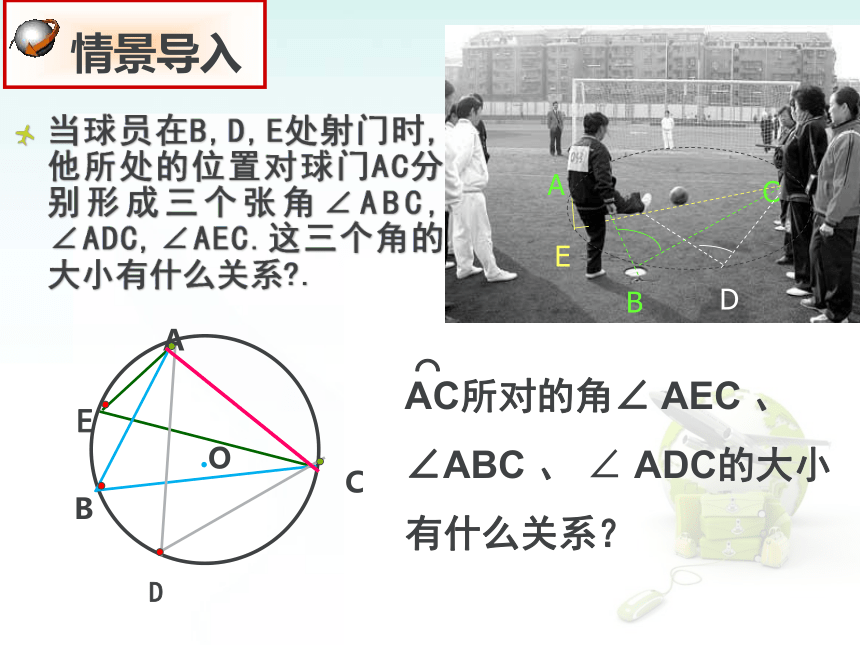
课件28张PPT。24.1.4 圆周角人教版九年级数学上册数学中的足球问题当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.ED
1．理解圆周角的定义,了解与圆心角的关系，会在具体情景中辨别圆周角．
2．掌握圆周角定理及推论，并会运用这些知识进行简单的计算和证明.教学目标:3. 学习中经历操作、观察、猜想、分析、交流、论证等数学活动，体验圆周角定理的探索过程，培养合情推理能力，发展自己的逻辑思维能力、推理论证能力和用几何语言表达的能力.【重点】
理解并掌握圆周角定理及推论
【难点】
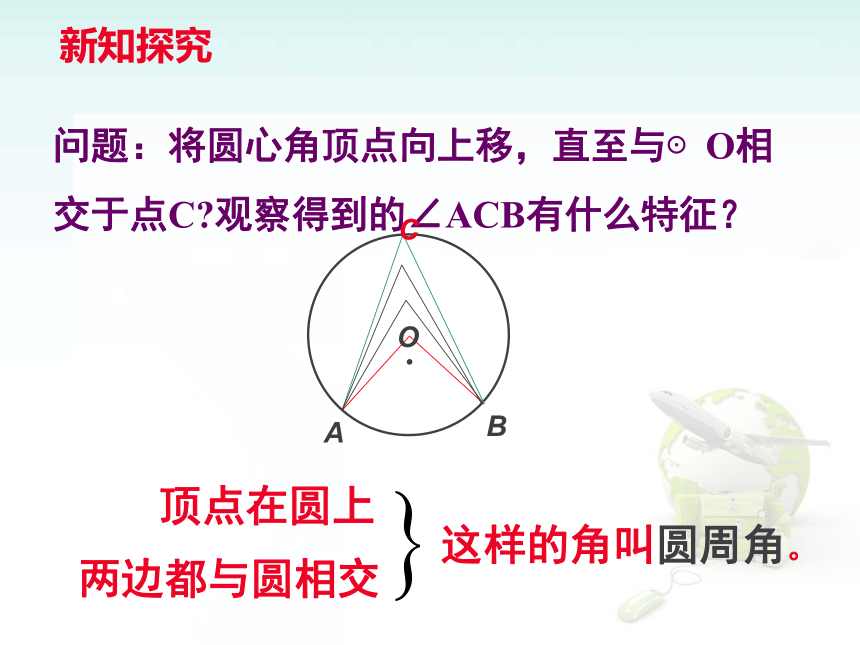
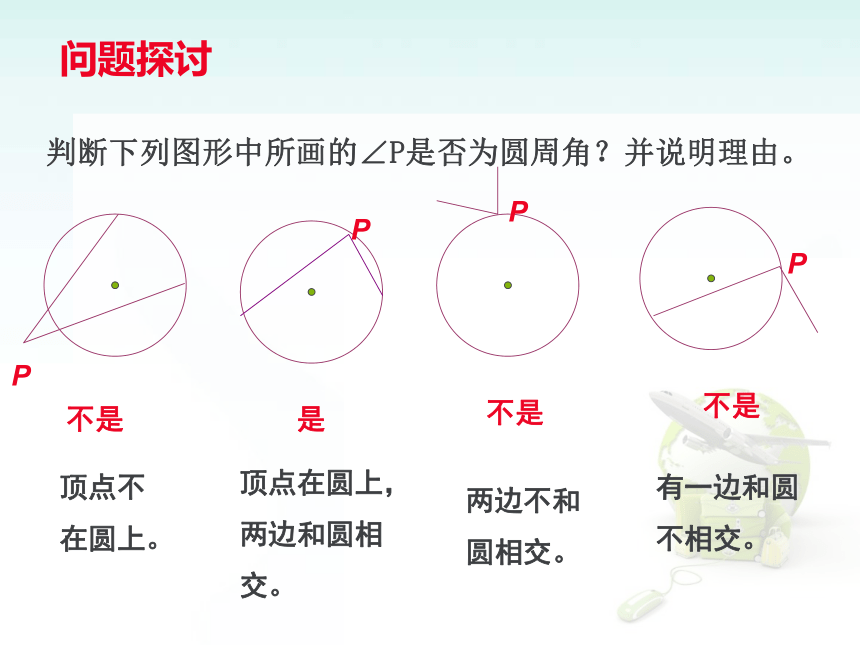
难点是圆周角定理的证明中采用的“分类讨论”及“由特殊到一般”的数学思想方法.知识回顾：什么叫圆心角?顶点在圆心的角叫圆心角.新知探究OA问题：将圆心角顶点向上移，直至与⊙O相交于点C?观察得到的∠ACB有什么特征？C 顶点在圆上 两边都与圆相交 这样的角叫圆周角。B问题探讨判断下列图形中所画的∠P是否为圆周角？并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上，两边和圆相交。两边不和圆相交。有一边和圆不相交。 总结归纳：
一个角是圆周角的条件：
①顶点在圆上；
②两边都和圆相交.有没有圆周角？有没有圆心角？它们有什么共同的特点？它们都对着同一条弧⌒⌒⌒ 下列图形中，哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。 图1图2 图3 图4图5探究一：你能画出同弧所对的圆周角和圆心角吗？你能证明你的发现（即同弧所对的圆周角度数等于这条弧所对的圆心角的一半）吗？ 证明你的猜想:
（1）首先考虑一种特殊情况：圆心
在∠BAC的一边上.
由于OA=OC因此∠C=∠BAC而∠BOC=∠BAC+∠C所以（2）一般情况，圆心在∠BAC的内部. 作直径AD.由于∠BAD= ∠BOD∠DAC= ∠DOC，所以∠BAD+∠DAC=
（∠BOD+∠DOC）即∠BAC= ∠BOCD（3）一般情况，圆心在∠BAC的外部.D作直径AD.由于∠DAB= ∠DOB∠DAC= ∠DOC，所以∠DAC-∠DAB= （∠DOC-∠DOB） 即∠BAC= ∠BOC圆周角定理：结论生成在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半。即∠BAC= ∠BOCABCO随堂演练：1.如图，已知在⊙ O 中，∠BOC =150°，求∠A.2.已知⊙O中弦AB的等于半径,求弦AB所对
的圆心角和圆周角的度数.圆心角为60°圆周角为30°或150°.3.如图，在⊙O中，ABC=50°，
则∠AOC等于（ ）
A、50°； B、80°；
C、90°； D、100°D1.半圆或直径所对的圆周角等于多少度？同弧或等弧所对的圆周角相等.
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是圆的直径.探究二：OABC2.90°的圆周角所对的弦是
否是直径？推论：当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.规律：都相等，都等于圆心角∠AOC的一半结论：同弧或等弧所对的圆周角相等。例1 如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB平分线交⊙O于D，求BC、AD、BD的长．四边形 ACBD的面积.又在Rt△ABD中，AD2+BD2=AB2，解：∵AB是直径，∴ ∠ACB= ∠ADB=90°．在Rt△ABC中，∵CD平分∠ACB，∴AD=BD.例题讲解:随堂演练1、如图，∠A=50°， ∠AOC=60 °
BD是⊙O的直径，则∠AEB等于（ ）
A、70°； B、110°；
C、90°； D、120°B2、如图，△ABC的顶点A、B、C
都在⊙O上，∠C＝30 °，AB＝2，
则⊙O的半径是 。解：连接OA、OB∵∠C=30 ° ，∴∠AOB=60 °又∵OA=OB ，∴△AOB是等边三角形∴OA=OB=AB=2，即半径为2。23.如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.40°500
(1)一个概念（圆周角） 内容小结(2)一个定理：
(3)二个推论：
一条弧所对的圆周角等于它所
对的圆心角的一半.1.同弧或等弧所对的圆周角相等.
2.半圆或直径所对的圆周角是直角，90°的圆周角所对的弦是直径.作业布置
九上数学课本P89.5；P90.13、14.再见！