3.2《解一元一次方程(一)——合并同类项与移项》课件
文档属性
| 名称 | 3.2《解一元一次方程(一)——合并同类项与移项》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-01 09:10:09 | ||
图片预览








文档简介
课件22张PPT。3.2解一元一次方程(一) ——合并同类项与移项学习目标:
1.怎样合并同类项?(ax=b的形式)
2.什么叫做移项,需要注意
什么?
3.掌握解方程的一般步骤
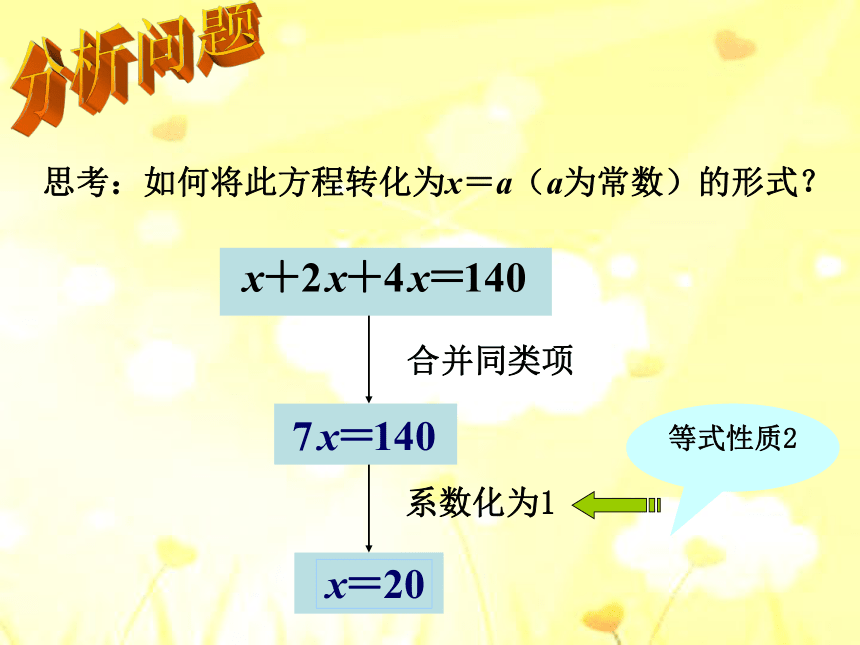
4.用方程解决实际问题思路是什么?问题1:某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?设去年购买计算机x台.设今年购买计算机x台.方法1:方法2:提出问题思考:如何将此方程转化为x=a(a为常数)的形式?合并同类项系数化为1等式性质2分析问题合并同类项,得系数化为1,得解:例把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?提出问题1、设未知数:设这个班有x名学生.2、找相等关系
这批书的总数是一个定值,表示它的两个等式相等3、列方程
3x+20 = 4x-25分析问题把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?每人分3本,共分出3x本,加上剩余的20本,这批书共 本.每人分4本,需要____ 本,减去缺的25本,
这批书共 本. 3x+204x4x-25提问:怎样解这个方程?它与上节课遇到的方程有何不同?3x+20 = 4x-25方程的两边都有含x的项(3x与4x)和不含字母的常数项(20与-25).3x+20=4x-253x+20-4x=4x-25-4x3x+20-4x= -253x+20-4x-20=-25-203x-4x=-25-20(合并同类项)(利用等式性质1) (利用等式性质1) (合并同类项)提问:如何才能使这个方程向x=a的形式转化?你发现了什么?3x +20 = 4x -253x-4x=-25 -20把等式一边的某一项改变符号后移到另一边,叫做移项.(教材P88)3x+20=4x-253x-4x=-25-20-x=-45X=45移项合并同类项系数化为1下面的框图表示了解这个方程的具体过程:通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式. 提问: “移项”起了什么作用?提问:以上解方程“移项”的依据是什么?移项的依据是等式的性质1例4某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t;如用新工艺,则废水排量要比环保限制的最大量少100t.新、旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
解:设新、旧工艺的废水排量分别为2xt和5xt.
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100.
移项,得5x-2x=100+200.
合并同类项,得3x=300.
系数化为1,得x=100.
所以2x=200,5x=500.
等号两边代表哪些数量?例:解下列方程 (1) 移项时应注意改变项的符号运用新知“移项”应注意什么?巩固练习解下列方程:(1)10x-3=9(2)6x-7=4x - 5一起来找茬下面方程的解法对吗?如果不对,应怎样改正?解方程:移项,得 合并同类项,得 系数化为1,得有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正好每条船坐9人,问:这个班共多少同学? 综合应用解法一:设船有x条.则
6(x+1)=9(x-1)
得出 x=5
6× (5+1)=36(人)
答:这个班共有36人.有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学? 1、已知2x+1与-12x+5的值是相反数,求x的值.拓展思维2、已知:y1 = 2x+1, y2 = 3 -x.当x取何值时, y1 = y2 ? 阿尔-花拉子米(约780——约850)中世纪阿拉伯数学家.出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献.它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响. 《对消与还原》 现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?“对消”与“还原”就是“合并”与“移项”1、今天你又学会了解方程的哪些方法?有哪些步聚?每一步的依据是什么?
2、今天讨论的问题中的相等关系又有何共同特点?
七嘴八舌说一说移项(等式的性质1)
合并(分配律)
系数化为1(等式的性质2)注意变号哦!表示同一量的两个不同式子相等. 再见
1.怎样合并同类项?(ax=b的形式)
2.什么叫做移项,需要注意
什么?
3.掌握解方程的一般步骤
4.用方程解决实际问题思路是什么?问题1:某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?设去年购买计算机x台.设今年购买计算机x台.方法1:方法2:提出问题思考:如何将此方程转化为x=a(a为常数)的形式?合并同类项系数化为1等式性质2分析问题合并同类项,得系数化为1,得解:例把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?提出问题1、设未知数:设这个班有x名学生.2、找相等关系
这批书的总数是一个定值,表示它的两个等式相等3、列方程
3x+20 = 4x-25分析问题把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?每人分3本,共分出3x本,加上剩余的20本,这批书共 本.每人分4本,需要____ 本,减去缺的25本,
这批书共 本. 3x+204x4x-25提问:怎样解这个方程?它与上节课遇到的方程有何不同?3x+20 = 4x-25方程的两边都有含x的项(3x与4x)和不含字母的常数项(20与-25).3x+20=4x-253x+20-4x=4x-25-4x3x+20-4x= -253x+20-4x-20=-25-203x-4x=-25-20(合并同类项)(利用等式性质1) (利用等式性质1) (合并同类项)提问:如何才能使这个方程向x=a的形式转化?你发现了什么?3x +20 = 4x -253x-4x=-25 -20把等式一边的某一项改变符号后移到另一边,叫做移项.(教材P88)3x+20=4x-253x-4x=-25-20-x=-45X=45移项合并同类项系数化为1下面的框图表示了解这个方程的具体过程:通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式. 提问: “移项”起了什么作用?提问:以上解方程“移项”的依据是什么?移项的依据是等式的性质1例4某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t;如用新工艺,则废水排量要比环保限制的最大量少100t.新、旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
解:设新、旧工艺的废水排量分别为2xt和5xt.
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100.
移项,得5x-2x=100+200.
合并同类项,得3x=300.
系数化为1,得x=100.
所以2x=200,5x=500.
等号两边代表哪些数量?例:解下列方程 (1) 移项时应注意改变项的符号运用新知“移项”应注意什么?巩固练习解下列方程:(1)10x-3=9(2)6x-7=4x - 5一起来找茬下面方程的解法对吗?如果不对,应怎样改正?解方程:移项,得 合并同类项,得 系数化为1,得有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正好每条船坐9人,问:这个班共多少同学? 综合应用解法一:设船有x条.则
6(x+1)=9(x-1)
得出 x=5
6× (5+1)=36(人)
答:这个班共有36人.有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学? 1、已知2x+1与-12x+5的值是相反数,求x的值.拓展思维2、已知:y1 = 2x+1, y2 = 3 -x.当x取何值时, y1 = y2 ? 阿尔-花拉子米(约780——约850)中世纪阿拉伯数学家.出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献.它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响. 《对消与还原》 现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?“对消”与“还原”就是“合并”与“移项”1、今天你又学会了解方程的哪些方法?有哪些步聚?每一步的依据是什么?
2、今天讨论的问题中的相等关系又有何共同特点?
七嘴八舌说一说移项(等式的性质1)
合并(分配律)
系数化为1(等式的性质2)注意变号哦!表示同一量的两个不同式子相等. 再见
