23.4 中位线课件
图片预览






文档简介
(共17张PPT)
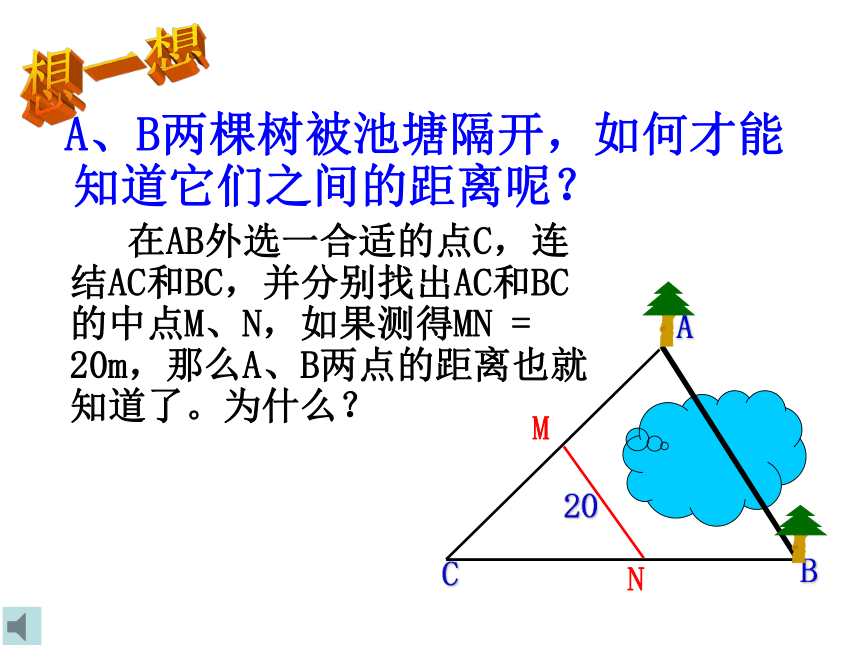
A、B两棵树被池塘隔开,如何才能知道它们之间的距离呢?
M
N
在AB外选一合适的点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离也就知道了。为什么?
C
B
A
20
学习目标:
1.理解三角形的中位线的概念;
2.探索并掌握三角形的中位线的性质;
3.会用三角形中位线的性质解决有关问题,感受数学的应用价值.
请同学们结合学习目标,提出自己心
中的疑问,看谁的问题更有探究价值?
学习目标:
1.理解三角形的中位线的概念;
2.探索并掌握三角形的中位线的性质;
3.会用三角形中位线的性质解决有关问题,感受数学的应用价值.
学而不疑则怠,疑而不探则空。
1.请同学们结合自探提示独立思考,找出相关内容。
2.在书上圈点批注,不确定的问题留待合探解决。
时间5分钟。
自探提示:
1.什么样的线是三角形的中位线?一个三角形有几条中位线?你能画出来吗?
2.三角形中位线有什么性质?几何语言如何表示?
3.三角形的中位线与中线有什么区别?
一条中位线与第三边上的中线有什么关系?
4.三角形的两条中线的交点有什么特别之处?
这个交点叫什么名字?
独学而无友,则孤陋而寡闻
将你的自学效果放在小组内交流一下;
将你在自学过程中不能独立解决的问题放在小组内讨论解决;
组长做好分工和记录。
自探提示:
1.什么是三角形的中位线?一个三角形有几条中位线?你能画出来吗?
2.三角形中位线有什么性质?几何语言如何表示?
3.三角形的中位线与中线有什么区别?
一条中位线与第三边上的中线有什么关系?
4.三角形的两条中线的交点有什么特别之处?
这个交点叫什么名字?
8/6
7/5
3/2
1/4
展(板)/评(口)
展示评价分工表
点评要求:
1、声音洪亮脱稿,注重自己的“教态”。
2、语言言简意赅,思路清晰,重点点评优缺点及总结方法规律。
3、非点评同学认真听讲,有疑问或见解及时提出来。
4、最后对展示同学打分,每题10分。
展 示题 目 展 示小 组 展 示方 式 评 价小 组 评价方式
1 第1组 板 书 第2组 口述
2 第3组 板 书 第4组 口述
3 第5组 板 书 第6组 口述
4 第7组 板 书 第8组 口述
展示要求:
排版整齐,书写快速工整,思路清晰,内容准确详细。
非展示同学继续在小组内讨论交流。
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
(1) △DEF的周长= cm
(2)你还能得到哪些结论?
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
试一试
疑是开山斧,探是深耕犁。
随着对本节知识的进一步理解,你又产生了哪些新的疑惑呢?请大胆提出来,我们共同探讨。
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
A
B
C
D
E
F
动动手
A
B
C
D
E
F
四边形BCFD是平行四边形吗?为什么?
探索
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,它是什么四边形?为什么?
H
D
C
B
A
E
F
G
动动脑
以下四边形的中点四边形是何种四边形呢?
A
B
C
H
D
E
F
G
D
B
C
A
H
E
F
G
A
B
C
H
D
E
F
G
菱形
矩形
正方形
矩形ABCD
菱形ABCD
正方形ABCD
动动眼
请学科班长对本节内容进行总结
1.三角形中位线是三角形中一种重要的线段,它与三角形中线不同。
2.三角形的中位线定理是三角形的一个重要性质定理。熟悉三角形中位线所在的图形的结构,注意定理的条件、结论,结论有两个,具体应用时,可视具体情况,选用其中一个关系或用两个关系。
1、必做题:习题23.4第2、3题
2、选做题:习题23.4第4题
A、B两棵树被池塘隔开,如何才能知道它们之间的距离呢?
M
N
在AB外选一合适的点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离也就知道了。为什么?
C
B
A
20
学习目标:
1.理解三角形的中位线的概念;
2.探索并掌握三角形的中位线的性质;
3.会用三角形中位线的性质解决有关问题,感受数学的应用价值.
请同学们结合学习目标,提出自己心
中的疑问,看谁的问题更有探究价值?
学习目标:
1.理解三角形的中位线的概念;
2.探索并掌握三角形的中位线的性质;
3.会用三角形中位线的性质解决有关问题,感受数学的应用价值.
学而不疑则怠,疑而不探则空。
1.请同学们结合自探提示独立思考,找出相关内容。
2.在书上圈点批注,不确定的问题留待合探解决。
时间5分钟。
自探提示:
1.什么样的线是三角形的中位线?一个三角形有几条中位线?你能画出来吗?
2.三角形中位线有什么性质?几何语言如何表示?
3.三角形的中位线与中线有什么区别?
一条中位线与第三边上的中线有什么关系?
4.三角形的两条中线的交点有什么特别之处?
这个交点叫什么名字?
独学而无友,则孤陋而寡闻
将你的自学效果放在小组内交流一下;
将你在自学过程中不能独立解决的问题放在小组内讨论解决;
组长做好分工和记录。
自探提示:
1.什么是三角形的中位线?一个三角形有几条中位线?你能画出来吗?
2.三角形中位线有什么性质?几何语言如何表示?
3.三角形的中位线与中线有什么区别?
一条中位线与第三边上的中线有什么关系?
4.三角形的两条中线的交点有什么特别之处?
这个交点叫什么名字?
8/6
7/5
3/2
1/4
展(板)/评(口)
展示评价分工表
点评要求:
1、声音洪亮脱稿,注重自己的“教态”。
2、语言言简意赅,思路清晰,重点点评优缺点及总结方法规律。
3、非点评同学认真听讲,有疑问或见解及时提出来。
4、最后对展示同学打分,每题10分。
展 示题 目 展 示小 组 展 示方 式 评 价小 组 评价方式
1 第1组 板 书 第2组 口述
2 第3组 板 书 第4组 口述
3 第5组 板 书 第6组 口述
4 第7组 板 书 第8组 口述
展示要求:
排版整齐,书写快速工整,思路清晰,内容准确详细。
非展示同学继续在小组内讨论交流。
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
(1) △DEF的周长= cm
(2)你还能得到哪些结论?
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
试一试
疑是开山斧,探是深耕犁。
随着对本节知识的进一步理解,你又产生了哪些新的疑惑呢?请大胆提出来,我们共同探讨。
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
A
B
C
D
E
F
动动手
A
B
C
D
E
F
四边形BCFD是平行四边形吗?为什么?
探索
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,它是什么四边形?为什么?
H
D
C
B
A
E
F
G
动动脑
以下四边形的中点四边形是何种四边形呢?
A
B
C
H
D
E
F
G
D
B
C
A
H
E
F
G
A
B
C
H
D
E
F
G
菱形
矩形
正方形
矩形ABCD
菱形ABCD
正方形ABCD
动动眼
请学科班长对本节内容进行总结
1.三角形中位线是三角形中一种重要的线段,它与三角形中线不同。
2.三角形的中位线定理是三角形的一个重要性质定理。熟悉三角形中位线所在的图形的结构,注意定理的条件、结论,结论有两个,具体应用时,可视具体情况,选用其中一个关系或用两个关系。
1、必做题:习题23.4第2、3题
2、选做题:习题23.4第4题
