2017-2018年湖北省仙桃市第十中学人教版九年级数学上册课件:25.1.1 随机事件 (共26张PPT)
文档属性
| 名称 | 2017-2018年湖北省仙桃市第十中学人教版九年级数学上册课件:25.1.1 随机事件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-01 11:39:59 | ||
图片预览







文档简介
课件26张PPT。第二十五章 概率的初步 “天有不测云” 原意是指刮风、下雨、阴天、晴天这些天气状况,人们事先很难预料.后来泛指世界上很多事情具有偶然性,人们不能事先判定这些事情是否会发生。25.1.1 随机事件思考:下列哪些现象是必然发生的,
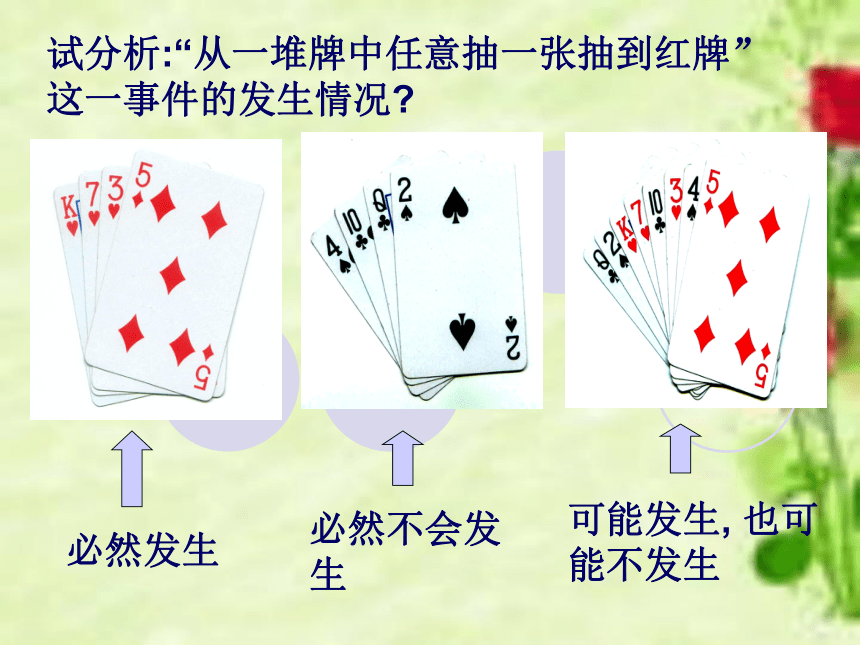
哪些现象是不可能发生的?(不可能发生)(必然发生)(必然发生)(不可能发生)试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?可能发生, 也可能不发生必然发生必然不会发生小明从盒中任意摸出一球,
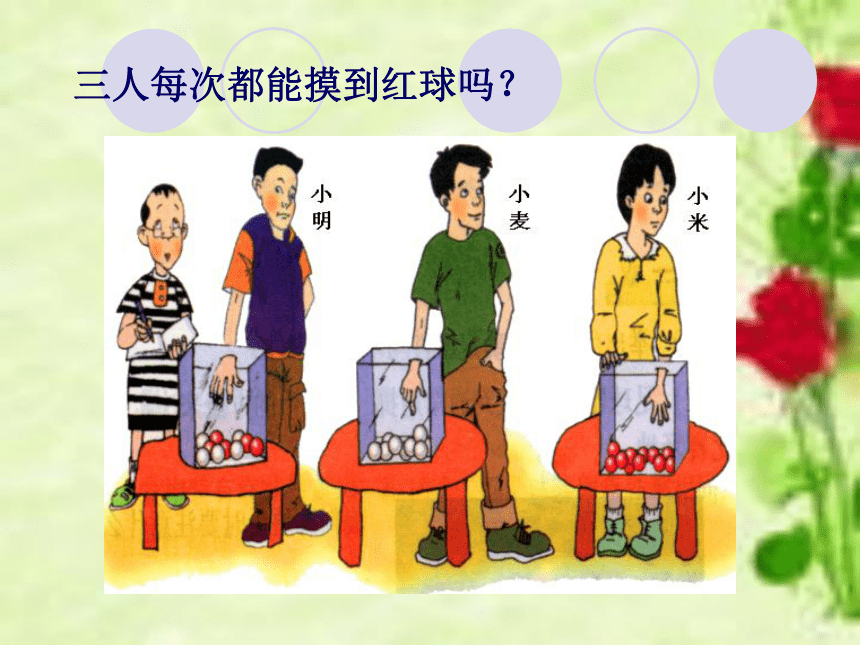
一定能摸到红球吗?小麦从盒中摸出的球一定是白球吗?小米从盒中摸出的球一定是红球吗?三人每次都能摸到红球吗? 在自然界和实际生活中,我们会遇到各种各样的现象.如果从结果能否预知的角度来看,可以分为两大类: 另一类现象的结果是无法预知的,即在一定的条件下,出现那种结果是无法预先确定的,这类现象称为随机现象. 一类现象的结果总是确定的,即在一定的条件下,它所出现的结果是可以预知的,这类现象称为确定性现象;在一定条件下:
必然会发生的事件叫做必然事件;必然不会发生的事件或者不可能发生的事件叫做不可能事件;可能会发生,也可能不发生的事件叫做不确定事件或随机事件.特征:事先不能预料即具有不确定性。5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签。(1)抽到的序号有几种可能的结果? (2)抽到的序号小于6吗? (3)抽到的序号会是0吗? (4)抽到的序号会是1吗? (5)请你用自己的语言叙述随机事件的定义活动1 小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1至6的点数。请考虑以下问题,掷一次骰子,观察骰子向上的一面: (1)可能出现哪些点数? (3)出现的点数会是7吗? (2)出现的点数大于0吗? (4)出现的点数会是4吗? 活动2随机事件练一练,看谁做得快:指出下列事件中,哪些是必然发生的,哪些是不可能
发生的,哪些是随机事件;
⑴通常加热到100℃时,水沸滕;
⑵篮球队员在罚球线上投篮时,未投中;
⑶掷一次骰子,向上的一面是6点;
⑷度量三角形的内角和,结果是360°;
⑸经过城西加油站路口,遇到红灯;
⑹某射击运动员射击一次,命中靶心。
(必然事件)(随机事件)(不可能事件)(随机事件)(随机事件)(随机事件) ⑴同一枚骰子连续掷两次,朝上一面出现点数之和为14.
⑵任意四边形的内角和都等于360°.
⑶一辆小汽车从面前经过,它的车牌号码为偶数.
⑷从一副完整扑克牌中任抽一张,它是草花.试一试1.指出下列事件是哪类事件(必然事件,不可能事件,随机事件)(必然事件)(不可能事件)(随机事件)(随机事件)议一议在我们生活中你还能举出必然事件,不可能事件和随机事件的实例吗? 生死签 相传古代有个国王,国王非常阴险而多疑,一位正直的大臣得罪了国王,被判死刑,这个国家世代沿袭着一条奇特的法规:凡是死囚,在临刑前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到死签,则立即处死,若抽到“生”签,则当场赦免。国王一心想处死大臣,与几个心腹密谋,想出一条毒计:暗中让执行官把“生死签”上都写成死,两死抽一,必死无疑。然而在断头台前,聪明的大臣迅速抽出一张签纸塞进嘴里,等到执行官反应过来,签纸早已吞下,大臣故作叹息说:“我听天意,将苦果吞下,只要看剩下的签是什么字就清楚了。”剩下的字当然写着“死”字,国王怕犯众怒,只好当众放了大臣。国王机关算尽,想让大臣死,反而搬起石头砸自己的脚,让机智的大臣死里逃生。
提出问题:(1)在法规中,大臣被处死是什么事件?
(2)在国王的阴谋中,大臣被处死是什么
事件?
(3)在大臣的计策中,大臣被处死是什么事件?事件发生的可能性要注意一定的条件。条件改变了,三类事件可以相互转化。小结:1.任抛一枚质地均匀的硬币,出现正面朝上,这是( ) 展示才智A2.下列事件是随机事件的是( )CB3 下列成语所描述的事件是必然事件是()
A:守株待兔
B:一箭双雕
C:水中捞月
D:瓮中捉鳖 D4 . 4个红球,3个白球,2个黑球放入一个袋子里,从中摸出8个球,恰好红球白球黑球都摸到,这事件是( )A.随机事件
B不可能事件
C必然事件
D很可能事件5 指出下列事件各是哪类事件?
①打开电视,正在播放节目《爸爸去哪儿》
②仙桃明天的最低气温是2℃
③一年有四季
④一袋中有若个干球,其中只有2个红球,小红从中摸出3个球,都是红球
⑤买一张电影票,座位号是奇数摸球试验:袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球。 (1)这个球是白球还是黑球?(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。思考:能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?学到了什么:必然发生的事件不可能发生的事件 随机事件事件确定事件定义:在一定条件下,有可能发生也有可能不发生称为随机事件 特征:事先不能预料即具有不确定性。探索是数学的生命线.再见
哪些现象是不可能发生的?(不可能发生)(必然发生)(必然发生)(不可能发生)试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?可能发生, 也可能不发生必然发生必然不会发生小明从盒中任意摸出一球,
一定能摸到红球吗?小麦从盒中摸出的球一定是白球吗?小米从盒中摸出的球一定是红球吗?三人每次都能摸到红球吗? 在自然界和实际生活中,我们会遇到各种各样的现象.如果从结果能否预知的角度来看,可以分为两大类: 另一类现象的结果是无法预知的,即在一定的条件下,出现那种结果是无法预先确定的,这类现象称为随机现象. 一类现象的结果总是确定的,即在一定的条件下,它所出现的结果是可以预知的,这类现象称为确定性现象;在一定条件下:
必然会发生的事件叫做必然事件;必然不会发生的事件或者不可能发生的事件叫做不可能事件;可能会发生,也可能不发生的事件叫做不确定事件或随机事件.特征:事先不能预料即具有不确定性。5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签。(1)抽到的序号有几种可能的结果? (2)抽到的序号小于6吗? (3)抽到的序号会是0吗? (4)抽到的序号会是1吗? (5)请你用自己的语言叙述随机事件的定义活动1 小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1至6的点数。请考虑以下问题,掷一次骰子,观察骰子向上的一面: (1)可能出现哪些点数? (3)出现的点数会是7吗? (2)出现的点数大于0吗? (4)出现的点数会是4吗? 活动2随机事件练一练,看谁做得快:指出下列事件中,哪些是必然发生的,哪些是不可能
发生的,哪些是随机事件;
⑴通常加热到100℃时,水沸滕;
⑵篮球队员在罚球线上投篮时,未投中;
⑶掷一次骰子,向上的一面是6点;
⑷度量三角形的内角和,结果是360°;
⑸经过城西加油站路口,遇到红灯;
⑹某射击运动员射击一次,命中靶心。
(必然事件)(随机事件)(不可能事件)(随机事件)(随机事件)(随机事件) ⑴同一枚骰子连续掷两次,朝上一面出现点数之和为14.
⑵任意四边形的内角和都等于360°.
⑶一辆小汽车从面前经过,它的车牌号码为偶数.
⑷从一副完整扑克牌中任抽一张,它是草花.试一试1.指出下列事件是哪类事件(必然事件,不可能事件,随机事件)(必然事件)(不可能事件)(随机事件)(随机事件)议一议在我们生活中你还能举出必然事件,不可能事件和随机事件的实例吗? 生死签 相传古代有个国王,国王非常阴险而多疑,一位正直的大臣得罪了国王,被判死刑,这个国家世代沿袭着一条奇特的法规:凡是死囚,在临刑前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到死签,则立即处死,若抽到“生”签,则当场赦免。国王一心想处死大臣,与几个心腹密谋,想出一条毒计:暗中让执行官把“生死签”上都写成死,两死抽一,必死无疑。然而在断头台前,聪明的大臣迅速抽出一张签纸塞进嘴里,等到执行官反应过来,签纸早已吞下,大臣故作叹息说:“我听天意,将苦果吞下,只要看剩下的签是什么字就清楚了。”剩下的字当然写着“死”字,国王怕犯众怒,只好当众放了大臣。国王机关算尽,想让大臣死,反而搬起石头砸自己的脚,让机智的大臣死里逃生。
提出问题:(1)在法规中,大臣被处死是什么事件?
(2)在国王的阴谋中,大臣被处死是什么
事件?
(3)在大臣的计策中,大臣被处死是什么事件?事件发生的可能性要注意一定的条件。条件改变了,三类事件可以相互转化。小结:1.任抛一枚质地均匀的硬币,出现正面朝上,这是( ) 展示才智A2.下列事件是随机事件的是( )CB3 下列成语所描述的事件是必然事件是()
A:守株待兔
B:一箭双雕
C:水中捞月
D:瓮中捉鳖 D4 . 4个红球,3个白球,2个黑球放入一个袋子里,从中摸出8个球,恰好红球白球黑球都摸到,这事件是( )A.随机事件
B不可能事件
C必然事件
D很可能事件5 指出下列事件各是哪类事件?
①打开电视,正在播放节目《爸爸去哪儿》
②仙桃明天的最低气温是2℃
③一年有四季
④一袋中有若个干球,其中只有2个红球,小红从中摸出3个球,都是红球
⑤买一张电影票,座位号是奇数摸球试验:袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球。 (1)这个球是白球还是黑球?(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。思考:能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?学到了什么:必然发生的事件不可能发生的事件 随机事件事件确定事件定义:在一定条件下,有可能发生也有可能不发生称为随机事件 特征:事先不能预料即具有不确定性。探索是数学的生命线.再见
同课章节目录
