2017-2018年湖南省岳阳市岳阳中学人教版数学九年级上册课件:24.1.3 弧、弦、圆心角 (共13张PPT)
文档属性
| 名称 | 2017-2018年湖南省岳阳市岳阳中学人教版数学九年级上册课件:24.1.3 弧、弦、圆心角 (共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-01 11:50:11 | ||
图片预览





文档简介
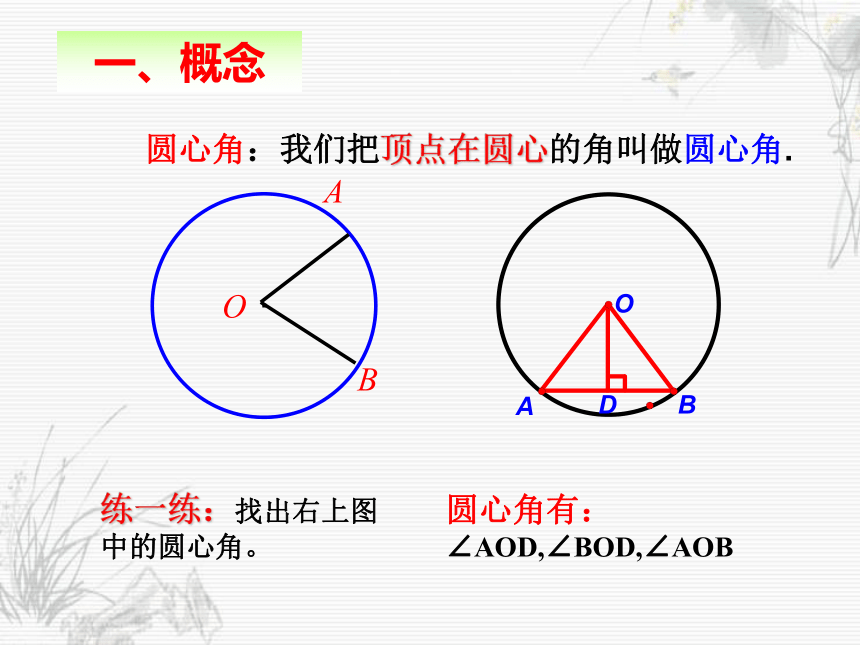
课件13张PPT。24.1.3 弧、弦、圆心角的关系☆复习引入1、圆是轴对称图形吗?它的对称轴是?垂径定理的内容是?我们是怎样证明垂径定理的? 圆是轴对称图形,对称轴是直径所在的直线。垂径定理是根据圆的轴对称性进行证明的。2、绕圆心转动一个圆,它会发生什么变化吗?圆是中心对称图形吗?它的对称中心在哪里? 它是不会发生变化的,我们称之为“圆具有旋转不变性”。圆是中心对称图形,它的对称中心是圆心。 今天这节课我们将运用圆的旋转不变性去探究弧、弦、圆心角的关系定理。· 圆心角:我们把顶点在圆心的角叫做圆心角.O一、概念练一练:找出右上图中的圆心角。圆心角有:∠AOD,∠BOD,∠AOB根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时, 显然∠AOB=∠A′OB′,射线 OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点 A与 A′重合,B与B′重合.·OAB·OABA′B′A′B′ 如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?二、探究 在等圆中,是否也能得到类似的结论呢?在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.弧、弦与圆心角的关系定理相等相等相等相等三、定理三、定理·OB′A′BA·O·B′O·A′B′O·BA′B′O1、2、3、 请利用右图用数学语言叙述一下我们刚学的三条定理。(见教材P83练习 1 ) 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?AB=CDAB=CD四、练习证明:∴ AB=AC.⊿ABC是等腰三角形又∴∠ACB=60°,∴ ⊿ABC是等边三角形 ,AB=BC=CA.∴ ∠AOB=∠BOC=∠AOC.·ABCO五、例题(见教材P83练习 2 )如图,AB是⊙O 的直径,
∠COD=35°,求∠AOE 的度数.解:六、练习七、思考 同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.八、作业1、教材87-88页
第2,3, 11题
2、完成练习册相关部分作业。谢谢指导!再见!
在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.弧、弦与圆心角的关系定理相等相等相等相等三、定理三、定理·OB′A′BA·O·B′O·A′B′O·BA′B′O1、2、3、 请利用右图用数学语言叙述一下我们刚学的三条定理。(见教材P83练习 1 ) 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?AB=CDAB=CD四、练习证明:∴ AB=AC.⊿ABC是等腰三角形又∴∠ACB=60°,∴ ⊿ABC是等边三角形 ,AB=BC=CA.∴ ∠AOB=∠BOC=∠AOC.·ABCO五、例题(见教材P83练习 2 )如图,AB是⊙O 的直径,
∠COD=35°,求∠AOE 的度数.解:六、练习七、思考 同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.八、作业1、教材87-88页
第2,3, 11题
2、完成练习册相关部分作业。谢谢指导!再见!
同课章节目录
