第20章数据的初步分析达标检测卷

第20章数据的初步分析达标检测卷
(150分，90分钟)
题　号
一
二
三
总　分
得　分
一、选择题(每题4分，共40分)
1．为了了解学生的考试成绩，数学老师将全班50名学生的期末数学考试成绩(满分100分)进行了统计分析，发现在60分以下的有3人，在60～70分的有8人，在70～80分的有13人，在80～90分的有11人，在90分以上(含90分)的有15人．则该统计过程中的数据11应属于的统计量是(　　)
A．众数
B．中位数
C．频数　　
D．频率
2．甲、乙两组数据的频数直方图如下，其中方差较大的一组是(　　)
A．甲
B．乙
C．一样大
D．不能确定
3．王老师对本班40名学生的血型进行了统计分析，列出如下的统计表，则本班A型血的人数是(　　)
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.16人
B．14人
C．4人
D．6人
4．某校组织了“讲文明、守秩序、迎南博”知识竞赛活动，从中抽取了7名同学的参赛成绩如下(单位：分)：80，90，70，100，60，80，80.则这组数据的中位数和众数分别是(　　)
A．90，80
B．70，80
C．80，80
D．100，80
5．今年，我省启动了“关爱留守儿童工程”．某村小学为了了解各年级留守儿童的数量，对一到六年级留守儿童数量进行了统计，得到每个年级的留守儿童人数分别为10，15，10，17，18，20.对于这组数据，下列说法错误的是(　　)
A．平均数是15
B．众数是10
C．中位数是17
D．方差是
6．小明在统计某市6月1日到10日每一天最高气温的变化情况时制作的折线图如图所示，则这10天最高气温的中位数和众数分别是(　　)
A．33℃，33℃
B．33℃，32℃
C．34℃，33℃
D．35℃，33℃
7．期中考试后，班里有两位同学议论他们所在小组同学的数学成绩，小明说：“我们组成绩是86分的同学最多”，小英说：“我们组的7位同学成绩排在最中间的恰好也是86分”．上面两位同学的话能反映出的统计量是(　　)
A．众数和平均数
B．平均数和中位数
C．众数和方差
D．众数和中位数
8．正整数4，5，5，x，y从小到大排列后，其中位数为4，如果这组数据唯一的众数是5，那么，所有满足条件的x，y中，x＋y的最大值是(　　)
A．3
B．4
C．5
D．6
9．如果一组数据a1，a2，a3，…，an的方差是2，那么一组新数据2a1，2a2，…，2an的方差是(　　)
A．2
B．4
C．8
D．16
10．甲、乙两班举行电脑汉字输入比赛，参赛学生每分钟输入汉字的个数统计结果如下表：
班级
参赛人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论：
①甲、乙两班学生汉字输入的平均水平相同；②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数不少于150为优秀)；③甲班成绩的波动比乙班大．上述结论正确的是(　　)
A．①②③
B．①②
C．①③
D．②③
二、填空题(每题5分，共20分)
11．为测试两种电子表的走时误差，进行了如下统计：
平均数
方差
甲
0.4
0.026
乙
0.4
0.137
则这两种电子表走时稳定的是______________．
12．两组数据：3，a，2b，5与a，6，b的平均数都是6，若将这两组数据合并为一组数据，则这组新数据的中位数为________．
13．已知一组数据1，2，3，…，n(从左往右数，第1个数是1，第2个数是2，第3个数是3，依次类推，第n个数是n)．设这组数据的各数之和是s，中位数是k，则s＝________(用只含有k的代数式表示)．
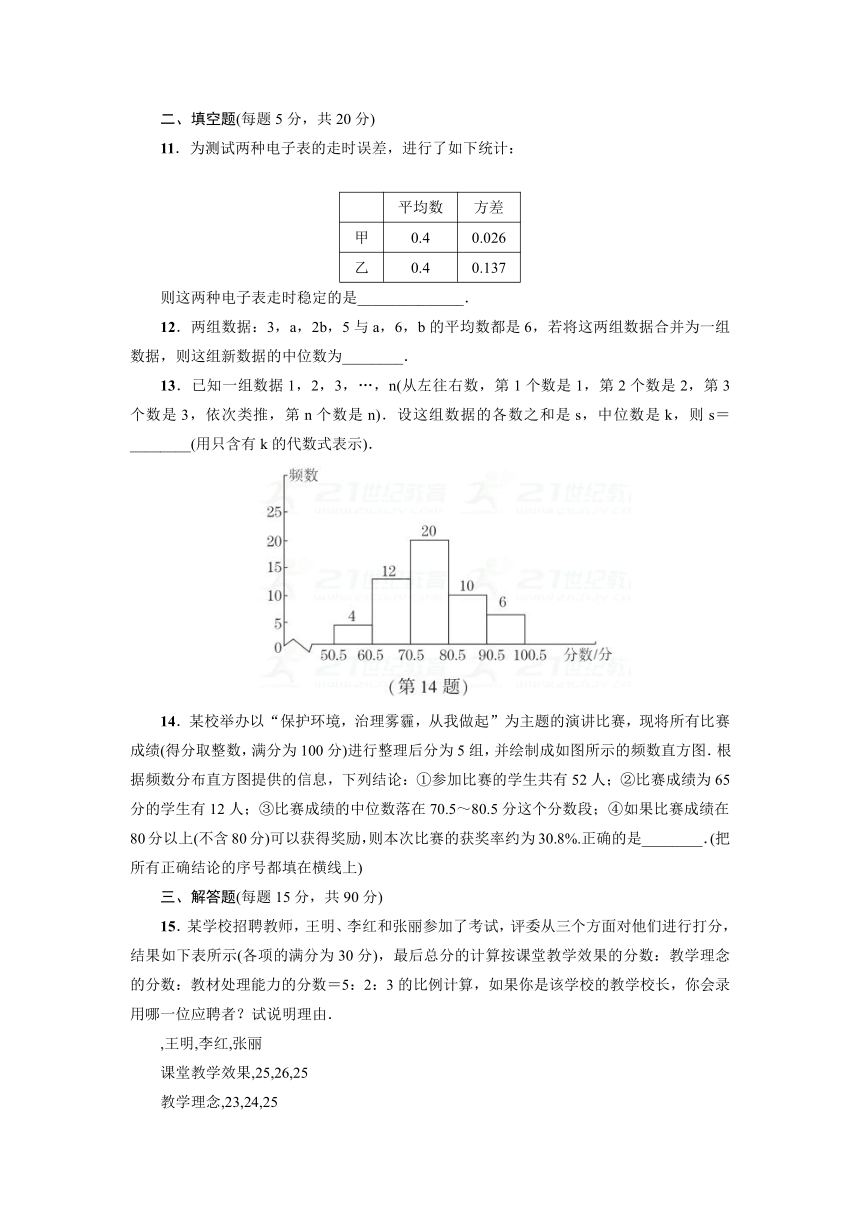
14．某校举办以“保护环境，治理雾霾，从我做起”为主题的演讲比赛，现将所有比赛成绩(得分取整数，满分为100分)进行整理后分为5组，并绘制成如图所示的频数直方图．根据频数分布直方图提供的信息，下列结论：①参加比赛的学生共有52人；②比赛成绩为65分的学生有12人；③比赛成绩的中位数落在70.5～80.5分这个分数段；④如果比赛成绩在80分以上(不含80分)可以获得奖励，则本次比赛的获奖率约为30.8%.正确的是________．(把所有正确结论的序号都填在横线上)
三、解答题(每题15分，共90分)
15．某学校招聘教师，王明、李红和张丽参加了考试，评委从三个方面对他们进行打分，结果如下表所示(各项的满分为30分)，最后总分的计算按课堂教学效果的分数：教学理念的分数：教材处理能力的分数＝5：2：3的比例计算，如果你是该学校的教学校长，你会录用哪一位应聘者？试说明理由．
,王明,李红,张丽
课堂教学效果,25,26,25
教学理念,23,24,25
教材处理能力,24,26,25
16．如图，是交警在一个路口统计的某个时段来往车辆的车速(单位：km/h)．
(1)计算这些车的平均速度．
(第16题)
(2)车速的众数是多少？
(3)车速的中位数是多少？
17．已知一组数据x1，x2，x3，…，xn的平均数是p，方差是q.
试证明：数据ax1＋b,
ax2＋b，ax3＋b，…，axn＋b的平均数是ap＋b，方差是a2q.
18．某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分．前6名选手的得分如下：
　　　　序号项目　　　　
1
2
3
4
5
6
笔试成绩/分
85
92
84
90
84
80
面试成绩/分
90
88
86
90
80
85
根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)．
(1)这6名选手笔试成绩的中位数是________分，众数是________分；
(2)现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比；
(3)求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选．
19．某农民在自己家承包的甲、乙两片荒山上各栽了200棵苹果树，成活率均为96%，现已挂果．他随意从甲山采摘了4棵树上的苹果，称得质量(单位：千克)分别为36，40，48，36；从乙山采摘了4棵树上的苹果，称得质量(单位：千克)分别为50，36，40，34，将这两组数据组成一个样本，回答下列问题：
(1)样本容量是多少？
(2)样本平均数是多少？并估算出甲、乙两山苹果的总产量；
(3)甲、乙两山哪个山上的苹果长势较整齐？
20．嘉兴市2010～2014年社会消费品零售总额及增速统计图如下：
请根据图中信息，解答下列问题：
(1)求嘉兴市2010～2014年社会消费品零售总额增速这组数据的中位数．
(2)求嘉兴市近三年(2012～2014年)的社会消费品零售总额这组数据的平均数．
(3)用适当的方法预测嘉兴市2015年社会消费品零售总额(只要求列出算式，不必计算出结果)．
(第20题)
答案
一、1.C　2.A　3.A　4.C　5.C
6．A　解析：将图中10个数据(单位：℃)按从小到大的顺序排列为：31，32，32，33，33，33，34，34，35，35，位于最中间的两个数都是33，故这组数据的中位数是33℃.这10个数据中，出现次数最多的是33，故众数是33℃.故选A.
7．D
8．C　解析：不妨设x9．C　10.A
二、11.甲　解析：比较统计表中甲、乙方差的大小，方差小的稳定．
12．6　解析：由题意得解得
∴这组新数据是3，4，5，6，8，8，8，其中位数是6.
13．2k2－k
14．①③④　解析：由题中的频数分布直方图可知，比赛成绩在50.5～60.5分数段的有4人，60.5～70.5分数段的有12人，70.5～80.5分数段的有20人，80.5～90.5分数段的有10人，90.5～100.5分数段的有6人，所以参加比赛的学生共有4＋12＋20＋10＋6＝52(人)，①正确；由已知条件和频数分布直方图得不出比赛成绩为65分的学生人数，②错误；将比赛成绩按从小到大的顺序排列，第26，27个数据都在70.5～80.5分数段内，故比赛成绩的中位数落在70.5～80.5分这个分数段，③正确；如果比赛成绩在80分以上(不含80分)可以获得奖励，则本次比赛的获奖率为×100%≈30.8%，④正确．
三、15.解：王明的成绩为＝24.3(分)，
李红的成绩为＝25.6(分)，
张丽的成绩为＝25(分)．
∵25.6>25>24.3，∴李红将被录用．
16．解：(1)这些车的平均速度是(40×2＋50×3＋60×4＋70×5＋80×1)÷(1＋2＋3＋4＋5)＝60(km/h)．
(2)车速的众数是70
km/h.
(3)车速的中位数是60
km/h.
解析：直接由条形图中数据信息求加权平均数，再根据图中具体数据和中位数、众数的定义，求出车速的众数和中位数．
17．证明：设数据ax1＋b,
ax2＋b,
ax3＋b，…，
axn＋b的平均数为M，方差为N.
由题意得p＝，q＝×[(x1－p)2＋(x2－p)2＋…＋(xn－p)2]．
因为M＝＝，所以M＝ap＋b，
N＝×[(ax1＋b－M)2＋(ax2＋b－M)2＋…＋(axn＋b－M)2]＝×[(ax1＋b－ap－b)2＋(ax2＋b－ap－b)2＋…＋(axn＋b－ap－b)2]＝
×[(ax1－ap)2＋(ax2－ap)2＋…＋(axn－ap)2]＝
×[(x1－p)2＋(x2－p)2＋…＋(xn－p)2]＝a2q.
即数据ax1＋b,
ax2＋b,
ax3＋b，…，
axn＋b的平均数是ap＋b，方差是a2q.
18．解：(1)84.5；84
(2)设笔试成绩和面试成绩所占的百分比分别是x，y，根据题意得：
解得
答：笔试成绩和面试成绩所占的百分比分别是40%，60%.
(3)2号选手的综合成绩是92×40%＋88×60%＝89.6(分)，
3号选手的综合成绩是84×40%＋86×60%＝85.2(分)，
4号选手的综合成绩是90×40%＋90×60%＝90(分)，
5号选手的综合成绩是84×40%＋80×60%＝81.6(分)，
6号选手的综合成绩是80×40%＋85×60%＝83(分)，
则综合成绩排序前两名的人选是4号和2号选手．
19．解：(1)样本容量为4＋4＝8.
(2)＝＝40.
甲、乙两山苹果的总产量约为400×40×96%＝15
360(千克)．
(3)∵甲＝×＝40，
∴s甲2＝×[(36－40)2＋(40－40)2＋(48－40)2＋(36－40)2]＝24.
∵乙＝×＝40，
∴s乙2＝×[(50－40)2＋(36－40)2＋(40－40)2＋(34－40)2]＝38.
∴s甲220．解：(1)数据从小到大排列为10.4%，12.5%，14.2%，15.1%，18.7%，则嘉兴市2010～2014年社会消费品零售总额增速这组数据的中位数为14.2%；
(2)嘉兴市近三年(2012～2014年)的社会消费品零售总额这组数据的平均数是：
(1
083.7＋1
196.9＋1
347.0)÷3＝1
209.2(亿元)；
(3)从增速中位数分析，嘉兴市2015年社会消费品零售总额为1
347×(1＋14.2%)亿元．(方法不唯一)