安徽省淮北市相山区2017--2018学年度九年级上学期第一次质量调研数学试题(含答案)
文档属性
| 名称 | 安徽省淮北市相山区2017--2018学年度九年级上学期第一次质量调研数学试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-01 00:00:00 | ||
图片预览



文档简介
相山区2017-2018学年度九年级联考
一
月考试卷
数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的.
1.下列函数中是二次函数的是(
)
A.
B.
C.
D.
2.已知(5,-1)是双曲线上的一点,则下列各点中不在该图象上的是(
)
A.(,-15)
B.(5,1)
C.
(-1,5)
D.(10,)
3.已知二次函数y=x2+x+c的图象与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是
A.(1,0)
B.(﹣1,0)
C.(2,0)
D.(﹣3,0)
4.下列关于抛物线 y= x 2 + 1 和 y=- x 2+ 2x-1的判断:①开口方向不同;②形状完全相同;③对称轴相同.其中正确的有(
)
A.0个
B.1个
C.2个
D.3个
5.若要从二次函数y=3x2的图象得到二次函数y=3(x+2)2-1的图象,则二次函数y=3x2的图象必须()
A.上移1个单位,右移2个单位;
B.下移1个单位,右移2个单位;
C.下移1个单位,左移2个单位;
D.上移2个单位,右移1个单位.
6.二次函数的图象与轴有交点,则的取值范围是(
)。
A.
B. 且
C.
D. 且
7.当温度不变时,气球内气体的气压P(单位: 是气体体积V(单位: 的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )
V(单位:
1
1.5
2
2.5
3
P(单位:
96
64
48
38.4
32
A.
B.
C.
D.
8.如图,铅球运动员掷铅球的高度m与水平距离m之间的函数关系式为.则该运动员此次掷铅球的成绩是(
)
A.
6m
B.
12m
C.
8m
D.
10m
9.已知抛物线与反比例函数的图像在第一象限有一个公共点,其横坐标为1,则一次函数的图像可能是(
)
10、已知函数 ,则使y=k成立的x值恰好有三个,则k的值为
0
B.
1
C.
2
D.
3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数,当a=________时,它是二次函数。
12.试写出一个开口方向向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式为______________.
13.如图,在平面直角坐标系中,函数(,常数)的图象经过点,,(),过点作轴的垂线,垂足为.若的面积为2,则点的坐标为
.
14.二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;
③abc<0;④4ac-b2<0;⑤当x≠2时,总有4a+2b>ax2+bx
其中正确的有
(填写正确结论的序号).
三、(本大题共2小题,每小题8分,满分16分)
15.已知y与成反比例,当时,.
(1)求这个函数的解析式.
(2)当,求x的值.
16、已知二次函数图象的顶点坐标为(1,-1),
且经过原点(0,0),求该函数的解析式.
四、(本大题共2小题,每小题8分,满分16分)
17、如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20
m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶
18、如图,已知反比例函数与一次函数的图象交于,。
(1)求、、的值。(2)求的面积。
(3)若,是反比例函数图象上的两点,且,,指出、各位于哪个象限,并简要说明理由。
五、(本大题共2小题,每小题10分,满分20分)
19、有一个运算装置,当输入值为x时.其输出值为y,且y是x的二次函数.已知输入值为﹣2,0,1时,相应的输出值分别为5,﹣3,﹣4.
(1)求二次函数的关系式;
(2)如图,在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时,输入值x的范围.
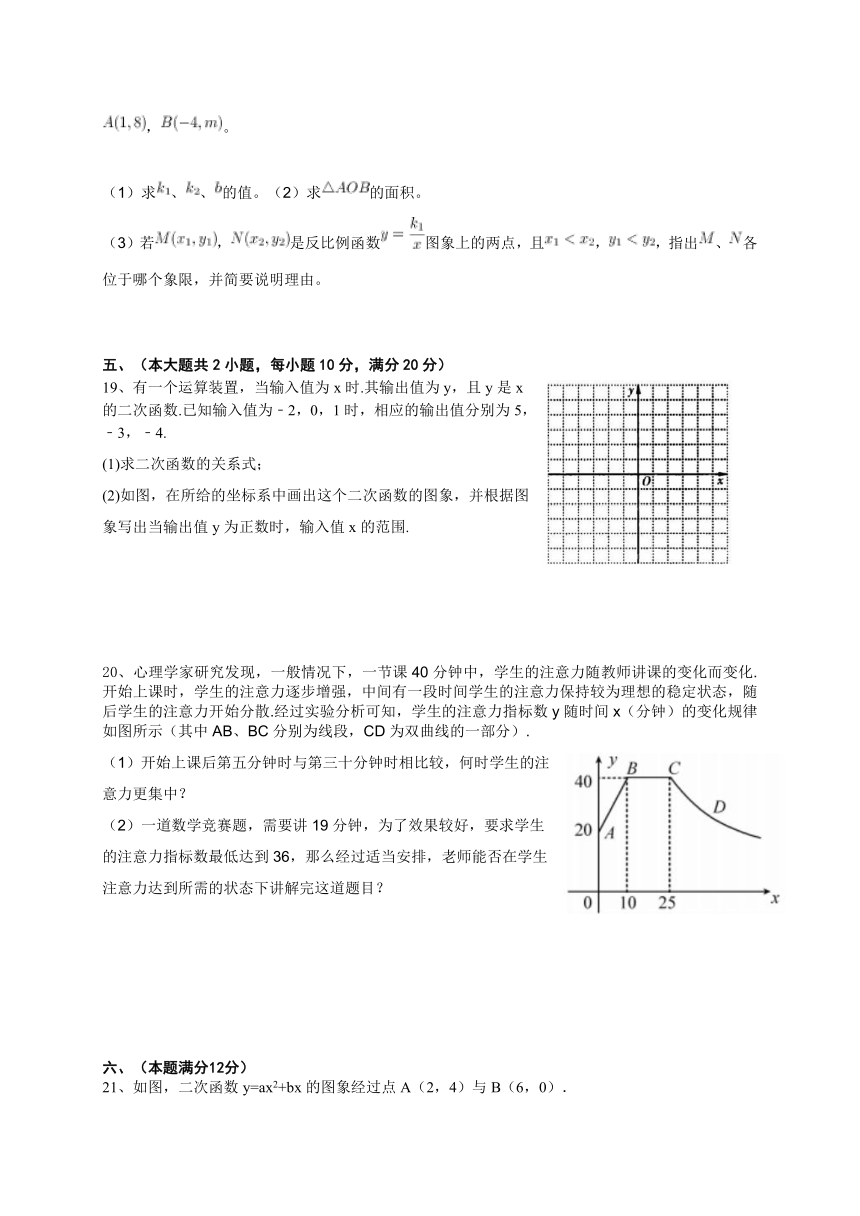
20、心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
六、(本题满分12分)
21、如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
七、(本题满分12分)
22.
若抛物线:(、、是常数,)与直线都经过轴上的一点,且抛物线的顶点在直线上,则称此直线与该抛物线具有“一带一路”关系,此时,直线叫做抛物线的“带线”,抛物线叫做直线的“路线”。
(1)若直线与抛物线具有“一带一路”关系,求、的值。
(2)若某“路线”的顶点在反比例函数的图象上,它的“带线”
的解析式为,求此路线的解析式。
八、(本题满分14分)
23.
东坡商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的销售单价P(元/千克)与时间t(天)之间的函数关系式为
,且其日销售量y(kg)与时间t(天)的关系如表
所示。
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少。
(2)问哪一天的销售利润最大,最大日销售利润是多少。
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润()给“精准扶贫”对象。现发现,在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围。
相山区2017-2018学年度第一学期九年级第一次月考
数学试卷参考答案
一、选择
1、C;2、B;3、D;4、A;5、C;6、D;7、D;8、D;9、B;10、
B;
第10题解析:y=k与每个抛物线有两个交点,在临界x=3时两个交点重合,所以共有三个交点,当x=3时得到y="3"
所以k=3
二、填空
11.a=0
12.答案不唯一,如y=x2 4x+3
13、B(3,)
14.
①②④⑤.
14.
解析:观察图形可知二次函数的图象过点(1,0),所以,所以①正确;又因为二次函数的图象过点(3,0),所以对称轴是x=2,所以,所以b=-4a,所以,所以②正确;因为抛物线开口向下,所以a<0,因为对称轴是x=2,所以a、b异号,所以b>0,因为抛物线与y轴交于负半轴,所以c<0,所以abc>0,所以③错误;因为二次函数的图象与z轴有两个交点,所以>0,所以,因此④正确;因为当x=2时,y有最大值,所以当时,总有,因此⑤正确;所以正确的有①②④⑤.
三、解答
15、解:(1)设,
把,代入解析式得,
计算得出:,
……………3分
则函数的解析式是;……………5分
(2)当时,,
计算得出:.
……………8分
16.解:设二次函数的解析式为y=a(x-1)2-1(a≠0),……………3分
∵函数图象经过原点(0,0),
∴a(0-1)2-1=0,……………6分
解得a=1,……………7分
∴该函数解析式为y=(x-1)2-1.……………8分
17.
(1)设所求抛物线的解析式为y=ax2,设D(5,b),则B(10,b-3),把D,B的坐标分别代入y=ax2,得
……………3分
解得
∴y=-.……………5分
(2)因为b=-1,所以=5(小时).
所以再持续5小时到达拱桥顶.……………8分
18.解(1)因为点在反比例函数上,代入得:,解得,又因为点在反比例函数上,所以。因为点,点在一次函数的图象上,所以代入点和点的坐标得:
,解得。综上所述,,,。…………3分
(2)如图所示,设一次函数的图象与轴交于点。由(1)得到一次函数的解析式为,令,解得,所以一次函数的图象与轴交于点,所以。……………6分
(3)由(1)得到反比例函数的解析式为,根据反比例函数的图象与性质可知在每个象限内随着的增大而减小,且第一象限的值大于,第三象限的值小于。因为,有,,所以点和不是位于同一象限,因此位于第三象限,位于第一象限。……………8分
19、解 :(1)设所求二次函数的解析式为y=ax2+bx+c,
把(-2,5)(0,-3)(1,-4)代入得
a( 2)2+b( 2)+c=5
a 02+b 0+c= 3
a+b+c= 4
解得a=1
b=-2
c=-3
故所求的解析式为:y=x2-2x-3.
……………4分
(2)函数图象如图所示……………7分
由图象可得,当输出值y为正数时,输入值x的取值范围是x<-1或x>3.
……………10分
四、解答题(每小题10分,共20分)
20、解:(1)设线段AB所在的直线解析式为y1=k1x+20,把B(10,40)代入得,k1=2,∴y1=2x+20.
……………2分
设C、D所在双曲线的解析式为y2=,把C(25,40)代入得,k2=1000,
∴y2=.……………4分
当x1=5时,y1=2×5+20=30,
当x2=30时,y2=,
∴y1<y2,
∴第30分钟注意力更集中.
……………6分
(2)令y1=36,
∴36=2x+20,
∴x1=8.
……………7分
令y2=36,∴,∴x2=.……………8分
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.………10分
五、解答题(每小题12分,共24分)
21、解:(1)将A(2,4)与B(6,0)代入y=ax2+bx,
得,解得:;……………4分
(2)如图,过A作x轴的垂线,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,
S△OAD=OD AD=×2×4=4;
S△ACD=AD CE=×4×(x﹣2)=2x﹣4;
S△BCD=BD CF=×4×(﹣x2+3x)=﹣x2+6x,
则S=S△OAD+S△ACD+S△BCD=4+2x﹣4﹣x2+6x=﹣x2+8x,……………9分
∴S关于x的函数表达式为S=﹣x2+8x(2<x<6),
∵S=﹣x2+8x=﹣(x﹣4)2+16,
∴当x=4时,四边形OACB的面积S有最大值,最大值为16.………
12分
22、解:(1)直线必经过轴上的点,将其代入抛物线,得。……………2分
则抛物线,顶点坐标是。将其代入直线,得,解得。……………4分
(2)设路线的解析式为。由题意可知,“路线”的顶点为反比例函数和“带线”的交点,将代入中得,整理得,解得或。……………7分
①当,将其代入直线的解析式中得交点为,则路线的解析式为。令,求得直线与轴的交点为。将代入路线的解析式,可得。……………9分
②当时,将其代入直线的解析式中得交点为,则路线的解析式为。将代入路线的解析式,可得。……………11分
综上所述,路线的解析式为或。………12分
23、解:(1)根据题意,设一次函数解释式为,将,代入解析式得,解得,所以日销量与时间的关系为,当时,。故在第天的日销量为千克。……………4分
(2)当时,利润,当时,利润取得最大值为元;……………6分
当时,利润,当时,利润随着的增大而减小,所以时,利润取得最大值为元。……………8分
因为,所以在第天时销售利润最大,最大利润为元。…………9分
(3)依题意,在前天中,利润,……………12分
其对称轴为,二次函数的系数,所以二次函数是开口向下的抛物线。要使利润随的增大而增大,由二次函数图象可知,,解得,又因为,所以。……………14分
一
月考试卷
数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的.
1.下列函数中是二次函数的是(
)
A.
B.
C.
D.
2.已知(5,-1)是双曲线上的一点,则下列各点中不在该图象上的是(
)
A.(,-15)
B.(5,1)
C.
(-1,5)
D.(10,)
3.已知二次函数y=x2+x+c的图象与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是
A.(1,0)
B.(﹣1,0)
C.(2,0)
D.(﹣3,0)
4.下列关于抛物线 y= x 2 + 1 和 y=- x 2+ 2x-1的判断:①开口方向不同;②形状完全相同;③对称轴相同.其中正确的有(
)
A.0个
B.1个
C.2个
D.3个
5.若要从二次函数y=3x2的图象得到二次函数y=3(x+2)2-1的图象,则二次函数y=3x2的图象必须()
A.上移1个单位,右移2个单位;
B.下移1个单位,右移2个单位;
C.下移1个单位,左移2个单位;
D.上移2个单位,右移1个单位.
6.二次函数的图象与轴有交点,则的取值范围是(
)。
A.
B. 且
C.
D. 且
7.当温度不变时,气球内气体的气压P(单位: 是气体体积V(单位: 的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )
V(单位:
1
1.5
2
2.5
3
P(单位:
96
64
48
38.4
32
A.
B.
C.
D.
8.如图,铅球运动员掷铅球的高度m与水平距离m之间的函数关系式为.则该运动员此次掷铅球的成绩是(
)
A.
6m
B.
12m
C.
8m
D.
10m
9.已知抛物线与反比例函数的图像在第一象限有一个公共点,其横坐标为1,则一次函数的图像可能是(
)
10、已知函数 ,则使y=k成立的x值恰好有三个,则k的值为
0
B.
1
C.
2
D.
3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数,当a=________时,它是二次函数。
12.试写出一个开口方向向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式为______________.
13.如图,在平面直角坐标系中,函数(,常数)的图象经过点,,(),过点作轴的垂线,垂足为.若的面积为2,则点的坐标为
.
14.二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;
③abc<0;④4ac-b2<0;⑤当x≠2时,总有4a+2b>ax2+bx
其中正确的有
(填写正确结论的序号).
三、(本大题共2小题,每小题8分,满分16分)
15.已知y与成反比例,当时,.
(1)求这个函数的解析式.
(2)当,求x的值.
16、已知二次函数图象的顶点坐标为(1,-1),
且经过原点(0,0),求该函数的解析式.
四、(本大题共2小题,每小题8分,满分16分)
17、如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20
m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶
18、如图,已知反比例函数与一次函数的图象交于,。
(1)求、、的值。(2)求的面积。
(3)若,是反比例函数图象上的两点,且,,指出、各位于哪个象限,并简要说明理由。
五、(本大题共2小题,每小题10分,满分20分)
19、有一个运算装置,当输入值为x时.其输出值为y,且y是x的二次函数.已知输入值为﹣2,0,1时,相应的输出值分别为5,﹣3,﹣4.
(1)求二次函数的关系式;
(2)如图,在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时,输入值x的范围.
20、心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分).
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
六、(本题满分12分)
21、如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
七、(本题满分12分)
22.
若抛物线:(、、是常数,)与直线都经过轴上的一点,且抛物线的顶点在直线上,则称此直线与该抛物线具有“一带一路”关系,此时,直线叫做抛物线的“带线”,抛物线叫做直线的“路线”。
(1)若直线与抛物线具有“一带一路”关系,求、的值。
(2)若某“路线”的顶点在反比例函数的图象上,它的“带线”
的解析式为,求此路线的解析式。
八、(本题满分14分)
23.
东坡商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的销售单价P(元/千克)与时间t(天)之间的函数关系式为
,且其日销售量y(kg)与时间t(天)的关系如表
所示。
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少。
(2)问哪一天的销售利润最大,最大日销售利润是多少。
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润()给“精准扶贫”对象。现发现,在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围。
相山区2017-2018学年度第一学期九年级第一次月考
数学试卷参考答案
一、选择
1、C;2、B;3、D;4、A;5、C;6、D;7、D;8、D;9、B;10、
B;
第10题解析:y=k与每个抛物线有两个交点,在临界x=3时两个交点重合,所以共有三个交点,当x=3时得到y="3"
所以k=3
二、填空
11.a=0
12.答案不唯一,如y=x2 4x+3
13、B(3,)
14.
①②④⑤.
14.
解析:观察图形可知二次函数的图象过点(1,0),所以,所以①正确;又因为二次函数的图象过点(3,0),所以对称轴是x=2,所以,所以b=-4a,所以,所以②正确;因为抛物线开口向下,所以a<0,因为对称轴是x=2,所以a、b异号,所以b>0,因为抛物线与y轴交于负半轴,所以c<0,所以abc>0,所以③错误;因为二次函数的图象与z轴有两个交点,所以>0,所以,因此④正确;因为当x=2时,y有最大值,所以当时,总有,因此⑤正确;所以正确的有①②④⑤.
三、解答
15、解:(1)设,
把,代入解析式得,
计算得出:,
……………3分
则函数的解析式是;……………5分
(2)当时,,
计算得出:.
……………8分
16.解:设二次函数的解析式为y=a(x-1)2-1(a≠0),……………3分
∵函数图象经过原点(0,0),
∴a(0-1)2-1=0,……………6分
解得a=1,……………7分
∴该函数解析式为y=(x-1)2-1.……………8分
17.
(1)设所求抛物线的解析式为y=ax2,设D(5,b),则B(10,b-3),把D,B的坐标分别代入y=ax2,得
……………3分
解得
∴y=-.……………5分
(2)因为b=-1,所以=5(小时).
所以再持续5小时到达拱桥顶.……………8分
18.解(1)因为点在反比例函数上,代入得:,解得,又因为点在反比例函数上,所以。因为点,点在一次函数的图象上,所以代入点和点的坐标得:
,解得。综上所述,,,。…………3分
(2)如图所示,设一次函数的图象与轴交于点。由(1)得到一次函数的解析式为,令,解得,所以一次函数的图象与轴交于点,所以。……………6分
(3)由(1)得到反比例函数的解析式为,根据反比例函数的图象与性质可知在每个象限内随着的增大而减小,且第一象限的值大于,第三象限的值小于。因为,有,,所以点和不是位于同一象限,因此位于第三象限,位于第一象限。……………8分
19、解 :(1)设所求二次函数的解析式为y=ax2+bx+c,
把(-2,5)(0,-3)(1,-4)代入得
a( 2)2+b( 2)+c=5
a 02+b 0+c= 3
a+b+c= 4
解得a=1
b=-2
c=-3
故所求的解析式为:y=x2-2x-3.
……………4分
(2)函数图象如图所示……………7分
由图象可得,当输出值y为正数时,输入值x的取值范围是x<-1或x>3.
……………10分
四、解答题(每小题10分,共20分)
20、解:(1)设线段AB所在的直线解析式为y1=k1x+20,把B(10,40)代入得,k1=2,∴y1=2x+20.
……………2分
设C、D所在双曲线的解析式为y2=,把C(25,40)代入得,k2=1000,
∴y2=.……………4分
当x1=5时,y1=2×5+20=30,
当x2=30时,y2=,
∴y1<y2,
∴第30分钟注意力更集中.
……………6分
(2)令y1=36,
∴36=2x+20,
∴x1=8.
……………7分
令y2=36,∴,∴x2=.……………8分
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.………10分
五、解答题(每小题12分,共24分)
21、解:(1)将A(2,4)与B(6,0)代入y=ax2+bx,
得,解得:;……………4分
(2)如图,过A作x轴的垂线,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,
S△OAD=OD AD=×2×4=4;
S△ACD=AD CE=×4×(x﹣2)=2x﹣4;
S△BCD=BD CF=×4×(﹣x2+3x)=﹣x2+6x,
则S=S△OAD+S△ACD+S△BCD=4+2x﹣4﹣x2+6x=﹣x2+8x,……………9分
∴S关于x的函数表达式为S=﹣x2+8x(2<x<6),
∵S=﹣x2+8x=﹣(x﹣4)2+16,
∴当x=4时,四边形OACB的面积S有最大值,最大值为16.………
12分
22、解:(1)直线必经过轴上的点,将其代入抛物线,得。……………2分
则抛物线,顶点坐标是。将其代入直线,得,解得。……………4分
(2)设路线的解析式为。由题意可知,“路线”的顶点为反比例函数和“带线”的交点,将代入中得,整理得,解得或。……………7分
①当,将其代入直线的解析式中得交点为,则路线的解析式为。令,求得直线与轴的交点为。将代入路线的解析式,可得。……………9分
②当时,将其代入直线的解析式中得交点为,则路线的解析式为。将代入路线的解析式,可得。……………11分
综上所述,路线的解析式为或。………12分
23、解:(1)根据题意,设一次函数解释式为,将,代入解析式得,解得,所以日销量与时间的关系为,当时,。故在第天的日销量为千克。……………4分
(2)当时,利润,当时,利润取得最大值为元;……………6分
当时,利润,当时,利润随着的增大而减小,所以时,利润取得最大值为元。……………8分
因为,所以在第天时销售利润最大,最大利润为元。…………9分
(3)依题意,在前天中,利润,……………12分
其对称轴为,二次函数的系数,所以二次函数是开口向下的抛物线。要使利润随的增大而增大,由二次函数图象可知,,解得,又因为,所以。……………14分
