13.4最短路径问题课件
图片预览






文档简介
课件25张PPT。13.4 课题学习
最短路径问题人民教育出版社义务教育教科书八年级数学(上册)
能利用轴对称解决简单的最短路径问题,体会图形的变化在解决最值问题中的作用,感悟转化思想.
学习重点:
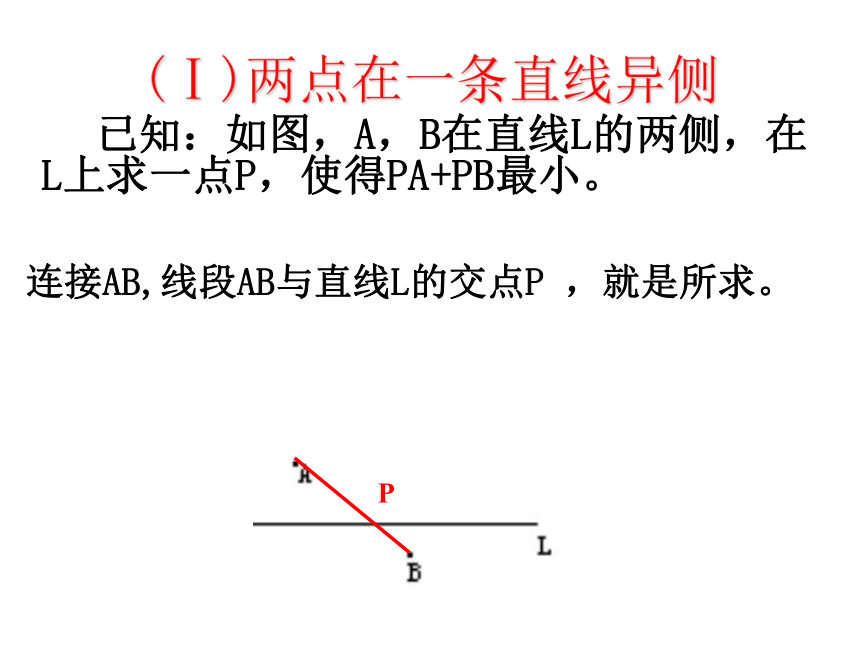
利用轴对称将最短路径问题转化为“两点之间,线段最短”问题. 学习目标 如图所示,从A地到B地有三条路可供选择,选走哪条路最近?你的理由是什么? 两点之间,线段最短(Ⅰ)两点在一条直线异侧 已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
P连接AB,线段AB与直线L的交点P ,就是所求。
思考???
为什么这样做就能得到最短距离呢?根据:两点之间线段最短.
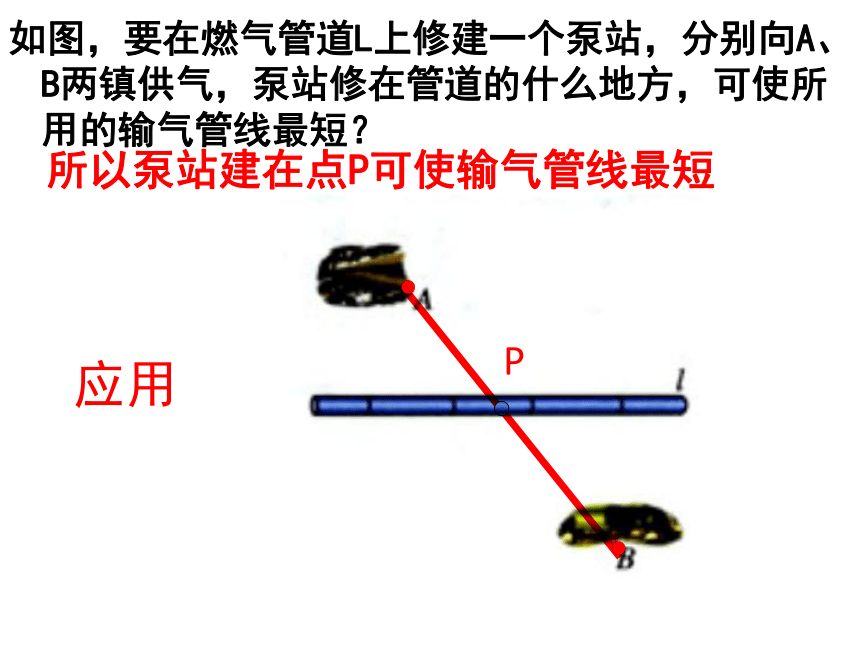
P如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?P所以泵站建在点P可使输气管线最短应用自学指导1认真阅读课本第85-86页问题2以上部分内容,并认真思考:
如何在L上找到点C,使得这个点到A的距离和到B点的距离之和最短?
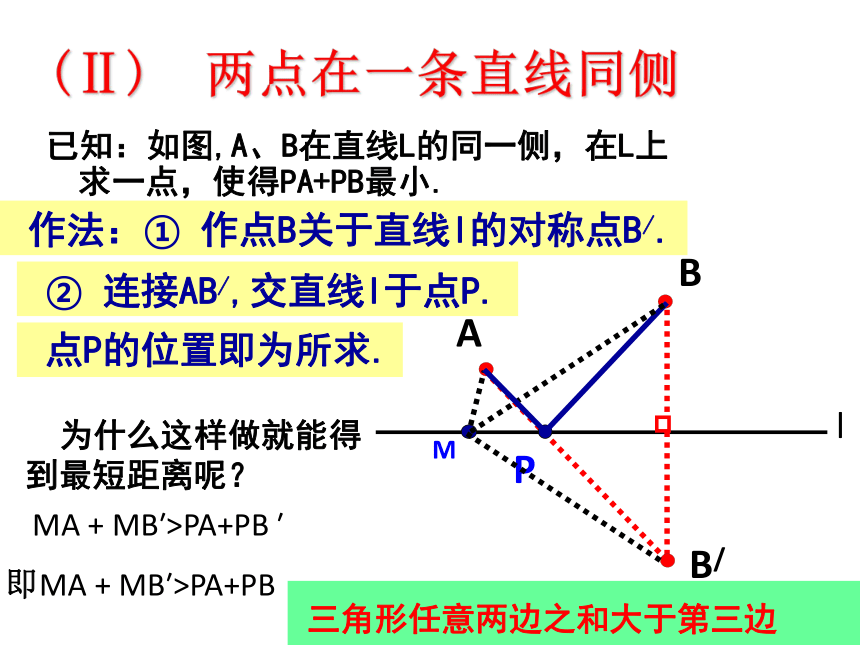
点P的位置即为所求. 作法:① 作点B关于直线l的对称点B/. ② 连接AB/,交直线l于点P.(Ⅱ) 两点在一条直线同侧
已知:如图,A、B在直线L的同一侧,在L上求一点,使得PA+PB最小.
为什么这样做就能得到最短距离呢?MA + MB′>PA+PB ′即MA + MB′>PA+PB 三角形任意两边之和大于第三边 问题:如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短. 请你自己动手 试一试!自学检测1只有A′ 、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C就是所求的点. 2. 如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点。
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D,则点D为建抽水站的位置。
ABa自学指导2 认真阅读课本第86-87页内容,并认真思考问题2:
如何在L上找到点C,使得这个点到A的距离和到B点的距离之和最短? 如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径AM、NB最短?(假设河的两岸是平行的直线,桥要与河垂直) 分析例题作法:1.将点B沿垂直与河岸的方向平移一个河宽到E,
2.连接AE交河对岸与点M,
则点M为建桥的位置,MN为所建的桥。
证明:由平移的性质,得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,
所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC.CD.DB.CE,
则AB两地的距离为:
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB >AM+MN+BN
所以桥的位置建在CD处,AB两地的路程最短。
A·BMNECD1、如图,张庄A、李庄B位于河沿的同侧,现要在
河沿g上修一提灌站C向张庄A、李庄B提水。当提
灌站修在河沿g的C处时,所用水管最短,为3千米。
已知BC的长为2千米,你能在图中找出张庄A的位
置吗?g.提灌站C·李庄B自学指导22、如图,小河边有两个村庄A,B,要在河边建一自
来水厂向村庄A与村庄B供水。
(1)若要使厂部到A,B村庄的距离相等,则应选择在
哪建厂?
(2)若要使厂部到A,B村的水管最省料,应建在什
么地方?··A村B村 小结这节课你学到了什么?例3.如图:一位将军骑马从驻地A出发,先牵马去草地
OM吃草,再牵马去河边ON喝水, 最后回到驻地A,
问:这位将军怎样走路程最短?OMN(三)二次轴对称:一点在两相交直线内部例3变式:已知P是△ABC的边BC上的点,
你能在AB、AC上分别确定一点Q和R,
使△PQR的周长最短吗?(三)二次轴对称:一点在两相交直线内部例4:如图,A为马厩,B为帐篷,将军某一天要
从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮助确定这一天的最短路线。(四)二次轴对称:两点在两相交直线内部例4变式:如图,OMCN是矩形的台球桌面,有黑、白两球分别位于B、A两点的位置上,
试问怎样撞击白球,使白球A依次碰撞球台边OM、ON后,反弹击中黑球?
(四)二次轴对称:两点在两相交直线内部......AA'BB'CDMON例4变式:(四)二次轴对称:两点在两相交直线内部两点在一条河两侧例5.如图:古希腊一位将军骑马从城堡A到城堡B,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥建在何处才能使将军从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)BA(五)造桥选址问题思维分析 1、如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?MN 2、利用线段公理解决问题我们遇到了什么障碍呢?
最短路径问题人民教育出版社义务教育教科书八年级数学(上册)
能利用轴对称解决简单的最短路径问题,体会图形的变化在解决最值问题中的作用,感悟转化思想.
学习重点:
利用轴对称将最短路径问题转化为“两点之间,线段最短”问题. 学习目标 如图所示,从A地到B地有三条路可供选择,选走哪条路最近?你的理由是什么? 两点之间,线段最短(Ⅰ)两点在一条直线异侧 已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
P连接AB,线段AB与直线L的交点P ,就是所求。
思考???
为什么这样做就能得到最短距离呢?根据:两点之间线段最短.
P如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?P所以泵站建在点P可使输气管线最短应用自学指导1认真阅读课本第85-86页问题2以上部分内容,并认真思考:
如何在L上找到点C,使得这个点到A的距离和到B点的距离之和最短?
点P的位置即为所求. 作法:① 作点B关于直线l的对称点B/. ② 连接AB/,交直线l于点P.(Ⅱ) 两点在一条直线同侧
已知:如图,A、B在直线L的同一侧,在L上求一点,使得PA+PB最小.
为什么这样做就能得到最短距离呢?MA + MB′>PA+PB ′即MA + MB′>PA+PB 三角形任意两边之和大于第三边 问题:如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短. 请你自己动手 试一试!自学检测1只有A′ 、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C就是所求的点. 2. 如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点。
作法:作点B关于直线 a 的对称点点C,连接AC交直线a于点D,则点D为建抽水站的位置。
ABa自学指导2 认真阅读课本第86-87页内容,并认真思考问题2:
如何在L上找到点C,使得这个点到A的距离和到B点的距离之和最短? 如图,A.B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径AM、NB最短?(假设河的两岸是平行的直线,桥要与河垂直) 分析例题作法:1.将点B沿垂直与河岸的方向平移一个河宽到E,
2.连接AE交河对岸与点M,
则点M为建桥的位置,MN为所建的桥。
证明:由平移的性质,得 BN∥EM 且BN=EM, MN=CD, BD∥CE, BD=CE,
所以A.B两地的距:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处,连接AC.CD.DB.CE,
则AB两地的距离为:
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△ACE中,∵AC+CE>AE,
∴AC+CE+MN>AE+MN,
即AC+CD+DB >AM+MN+BN
所以桥的位置建在CD处,AB两地的路程最短。
A·BMNECD1、如图,张庄A、李庄B位于河沿的同侧,现要在
河沿g上修一提灌站C向张庄A、李庄B提水。当提
灌站修在河沿g的C处时,所用水管最短,为3千米。
已知BC的长为2千米,你能在图中找出张庄A的位
置吗?g.提灌站C·李庄B自学指导22、如图,小河边有两个村庄A,B,要在河边建一自
来水厂向村庄A与村庄B供水。
(1)若要使厂部到A,B村庄的距离相等,则应选择在
哪建厂?
(2)若要使厂部到A,B村的水管最省料,应建在什
么地方?··A村B村 小结这节课你学到了什么?例3.如图:一位将军骑马从驻地A出发,先牵马去草地
OM吃草,再牵马去河边ON喝水, 最后回到驻地A,
问:这位将军怎样走路程最短?OMN(三)二次轴对称:一点在两相交直线内部例3变式:已知P是△ABC的边BC上的点,
你能在AB、AC上分别确定一点Q和R,
使△PQR的周长最短吗?(三)二次轴对称:一点在两相交直线内部例4:如图,A为马厩,B为帐篷,将军某一天要
从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮助确定这一天的最短路线。(四)二次轴对称:两点在两相交直线内部例4变式:如图,OMCN是矩形的台球桌面,有黑、白两球分别位于B、A两点的位置上,
试问怎样撞击白球,使白球A依次碰撞球台边OM、ON后,反弹击中黑球?
(四)二次轴对称:两点在两相交直线内部......AA'BB'CDMON例4变式:(四)二次轴对称:两点在两相交直线内部两点在一条河两侧例5.如图:古希腊一位将军骑马从城堡A到城堡B,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥建在何处才能使将军从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)BA(五)造桥选址问题思维分析 1、如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?MN 2、利用线段公理解决问题我们遇到了什么障碍呢?
