12.2.3 三角形全等的判定(AAS,ASA) 课件
文档属性
| 名称 | 12.2.3 三角形全等的判定(AAS,ASA) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 671.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-03 21:26:06 | ||
图片预览



文档简介
课件11张PPT。12.2.3 三角形全等的判定
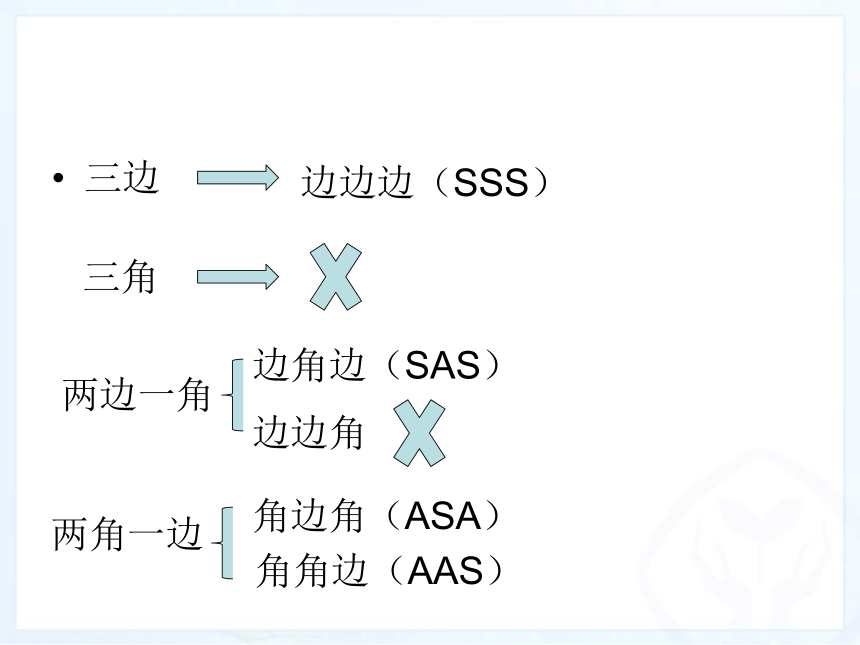
(ASA,AAS)主讲人:陈建华三边边边边(SSS) 三角两边一角边角边(SAS)边边角两角一边角边角(ASA)角角边(AAS)
1.探索并正确理解“ASA”和“AAS”判定方法.
2.会用“ASA”和“AAS”判定方法证明两个三角
形全等.
理解两种判定方法,并掌握用这两种方法证明两个
三角形全等. 学习目标: 学习重点:
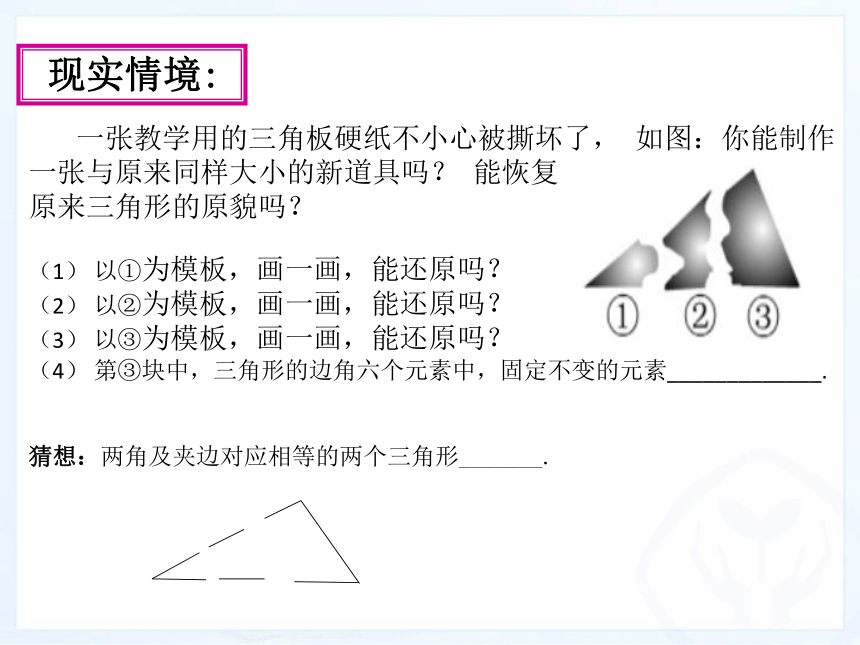
一张教学用的三角板硬纸不小心被撕坏了, 如图:你能制作一张与原来同样大小的新道具吗? 能恢复
原来三角形的原貌吗?
(1) 以①为模板,画一画,能还原吗?
(2) 以②为模板,画一画,能还原吗?
(3) 以③为模板,画一画,能还原吗?
(4) 第③块中,三角形的边角六个元素中,固定不变的元素_____________.
猜想:两角及夹边对应相等的两个三角形_______.
现实情境: 问题1 先在一张纸上画一个△ABC,然后在另一
张纸上画△DEF,使EF =BC,∠E =∠B,∠F =∠C.
△ABC 和△DEF 能重合吗?根据你画的两个三角形
及结果,你能得到又一个判定两个三角形全等的方法
吗? 两角和它们的夹边分别相等的两个三角形全等(
简称为“角边角”或“ASA”).动手画图,探究“ASA”判定方法适时引申,探究“AAS”判定方法 问题2 解答下面问题,你能获得什么结论?如图,
在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF,
△ABC 与△DEF 全等吗?你能利用“ASA”证明你的
结论吗?应用“ASA” 判定方法,解决实际问题 问题3 如图,小明、小强一起踢球,不小心把一
块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔
偿.你能告诉他们只带其中哪一块去玻璃店,就可以买
到一块完全一样的玻璃吗?例题示范,巩固新知证明:在△ABE 和△ACD 中,∴ △ABE ≌△ACD(ASA).
∴ AE =AD. 例1 如图,点D 在AB上,点E 在AC上,BA =AC,
∠B =∠C.求证:AD =AE. 课堂练习 练习 如图,E,F 在线段AC上,AD∥CB,AE =
CF.若∠B =∠D,求证:DF =BE.证明:∵ AD∥CB ,∴∠A=∠C.
∵ AE =CF ,∴ AF =CE.
在△ADF 和△CBE 中,∴ △ADF ≌△CBE(AAS).
∴ DF =BE.当堂检测课堂小结(1)本节课学习了几种判断两个三角形全等的方法?
分别是什么?它们之间有什么共同点和区别?
(2)本节课学习的两种方法能否用“两角一边相等,
则三角形全等” 来代替?
(ASA,AAS)主讲人:陈建华三边边边边(SSS) 三角两边一角边角边(SAS)边边角两角一边角边角(ASA)角角边(AAS)
1.探索并正确理解“ASA”和“AAS”判定方法.
2.会用“ASA”和“AAS”判定方法证明两个三角
形全等.
理解两种判定方法,并掌握用这两种方法证明两个
三角形全等. 学习目标: 学习重点:
一张教学用的三角板硬纸不小心被撕坏了, 如图:你能制作一张与原来同样大小的新道具吗? 能恢复
原来三角形的原貌吗?
(1) 以①为模板,画一画,能还原吗?
(2) 以②为模板,画一画,能还原吗?
(3) 以③为模板,画一画,能还原吗?
(4) 第③块中,三角形的边角六个元素中,固定不变的元素_____________.
猜想:两角及夹边对应相等的两个三角形_______.
现实情境: 问题1 先在一张纸上画一个△ABC,然后在另一
张纸上画△DEF,使EF =BC,∠E =∠B,∠F =∠C.
△ABC 和△DEF 能重合吗?根据你画的两个三角形
及结果,你能得到又一个判定两个三角形全等的方法
吗? 两角和它们的夹边分别相等的两个三角形全等(
简称为“角边角”或“ASA”).动手画图,探究“ASA”判定方法适时引申,探究“AAS”判定方法 问题2 解答下面问题,你能获得什么结论?如图,
在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF,
△ABC 与△DEF 全等吗?你能利用“ASA”证明你的
结论吗?应用“ASA” 判定方法,解决实际问题 问题3 如图,小明、小强一起踢球,不小心把一
块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔
偿.你能告诉他们只带其中哪一块去玻璃店,就可以买
到一块完全一样的玻璃吗?例题示范,巩固新知证明:在△ABE 和△ACD 中,∴ △ABE ≌△ACD(ASA).
∴ AE =AD. 例1 如图,点D 在AB上,点E 在AC上,BA =AC,
∠B =∠C.求证:AD =AE. 课堂练习 练习 如图,E,F 在线段AC上,AD∥CB,AE =
CF.若∠B =∠D,求证:DF =BE.证明:∵ AD∥CB ,∴∠A=∠C.
∵ AE =CF ,∴ AF =CE.
在△ADF 和△CBE 中,∴ △ADF ≌△CBE(AAS).
∴ DF =BE.当堂检测课堂小结(1)本节课学习了几种判断两个三角形全等的方法?
分别是什么?它们之间有什么共同点和区别?
(2)本节课学习的两种方法能否用“两角一边相等,
则三角形全等” 来代替?
