2017-2018年甘肃省天水市第三中学高中数学必修4课件:1.6三角函数模型的简单应用 (共23张PPT)
文档属性
| 名称 | 2017-2018年甘肃省天水市第三中学高中数学必修4课件:1.6三角函数模型的简单应用 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 87.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-06 14:03:22 | ||
图片预览






文档简介
课件23张PPT。1.6 三角函数模型
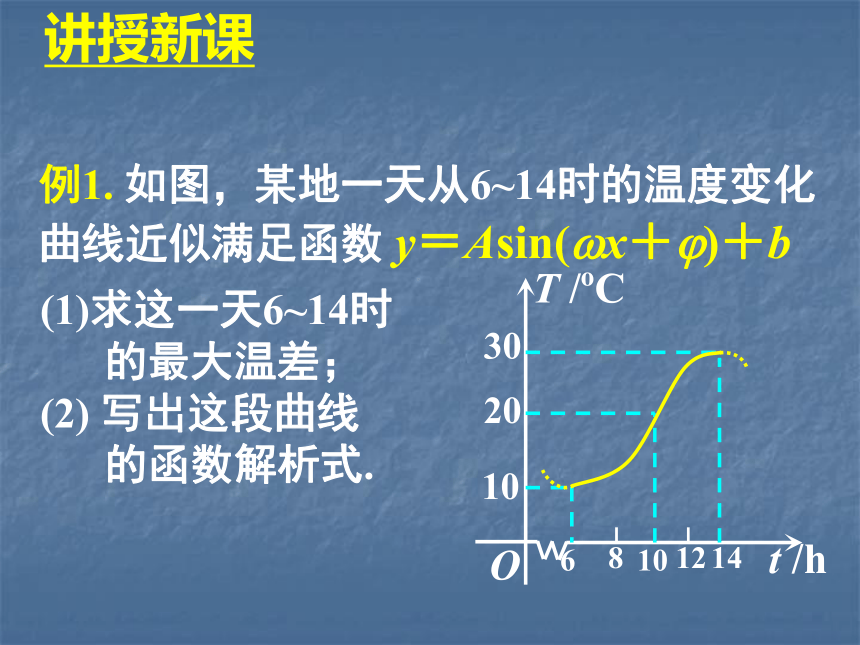
的简单应用讲授新课例1. 如图,某地一天从6~14时的温度变化
曲线近似满足函数 y=Asin(?x+?)+b求这一天6~14时
的最大温差;
(2) 写出这段曲线
的函数解析式.讲授新课例1. 如图,某地一天从6~14时的温度变化
曲线近似满足函数 y=Asin(?x+?)+b求这一天6~14时
的最大温差;
(2) 写出这段曲线
的函数解析式.一、根据图象建立函数解析式讲授新课一、根据图象建立函数解析式 小结:利用函数的模型(函数的
图象)解决问题,根据图象建立函数
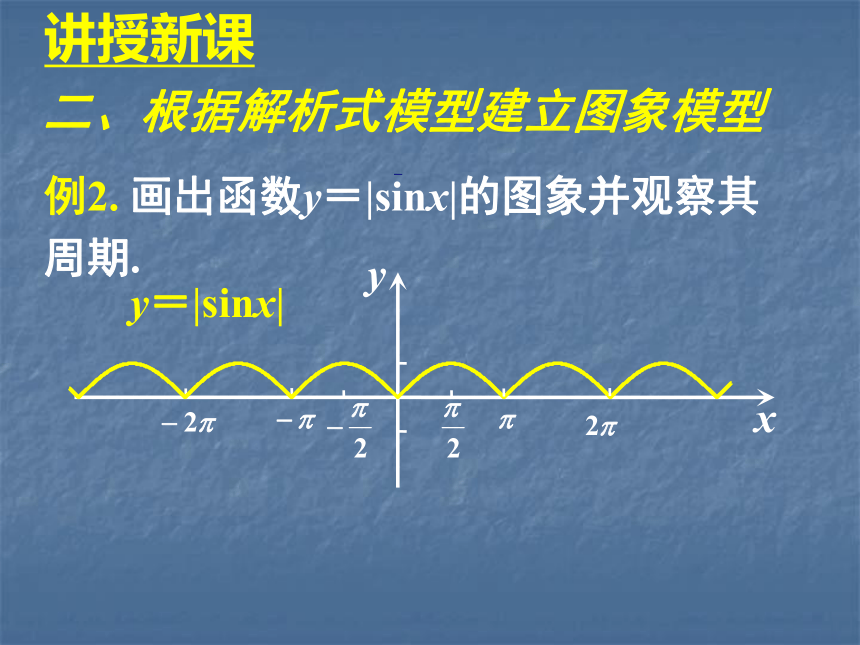
解析式.例2. 画出函数y=|sinx|的图象并观察其
周期.讲授新课例2. 画出函数y=|sinx|的图象并观察其
周期.二、根据解析式模型建立图象模型讲授新课讲授新课例2. 画出函数y=|sinx|的图象并观察其
周期.二、根据解析式模型建立图象模型讲授新课 小结:利用函数解析式模型建立
函数图象模型,并根据图象认识性质.二、根据解析式模型建立图象模型例2. 画出函数y=|sinx|的图象并观察其
周期.讲授新课例3. 如图,设地球表面某地正午太阳高度角为?,?为此时太阳直射纬度,?为该地的纬度值,那么这三个量之间的关系是? =90o-|? -? |.当地夏半年?取正值,冬半年?取负值. 如果在北京地区(纬度数约为北纬40o)的一
幢高为h0的楼房北面盖一
新楼,要使新楼一层正午
的太阳全年不被前
面的楼房遮挡,两
楼的距离不应小于
多少?讲授新课例3. 如图,设地球表面某地正午太阳高度角为?,?为
此时太阳直射纬度,?为该地的纬度值,那么这三个
量之间的关系是? =90o-|? -? |.当地夏半年?取正值,
冬半年?取负值. 如果在北京地区(纬度数约为北纬40o)的一幢高为
h0的楼房北面盖一新楼,要使新楼一层正午的太阳全
年不被前面的楼房遮挡,两楼的距离不应小于多少?|?-|?太阳光? -??讲授新课例4. 下面是某港口在某季节每天的时间与水深
的关系表:选用一个函数来近似描述这个港口的水深
与时间的函数关系,并给出整点时的水深的
近似数值(精确到0.001).讲授新课问题1:观察上表的数据,你发现了
什么规律?讲授新课问题1:观察上表的数据,你发现了
什么规律?问题2:根据数据作出散点图. 观察图形,
你认为可以用怎样的函数模型刻
画其中的规律?讲授新课问题1:观察上表的数据,你发现了
什么规律?问题3:能根据函数模型求整点时的水深
吗?问题2:根据数据作出散点图. 观察图形,
你认为可以用怎样的函数模型刻
画其中的规律?讲授新课例4. 下面是某港口在某季节每天的时间与水深
的关系表:(2) 一条货船的吃水深度(船底与水面的距离)为
4米,安全条例规定至少要有1.5米的安全间隙
(船底与洋底的距离) ,该船何时能进入港口?
在港口能呆多久?讲授新课例4. 下面是某港口在某季节每天的时间与水深
的关系表:(3) 若某船的吃水深度为4米,安全间隙为1.5米,
该船在2:00开始卸货,吃水深度以每小时0.3米
的速度减少,那么该船在什么时间必须停止卸
货,将船驶向较深的水域?讲授新课 小结:你能概括出建立三角函数模型
解决实际问题的基本步骤吗?课堂小结1. 三角函数模型应用基本步骤:
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
(2)根据解析式作出图象;
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
(2)根据解析式作出图象;
(3)将实际问题抽象为与三角函数有关
的简单函数模型.
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
(2)根据解析式作出图象;
(3)将实际问题抽象为与三角函数有关
的简单函数模型.
2. 利用收集到的数据作出散点图,并
根据散点图进行函数拟合,从而得到
函数模型.课后作业
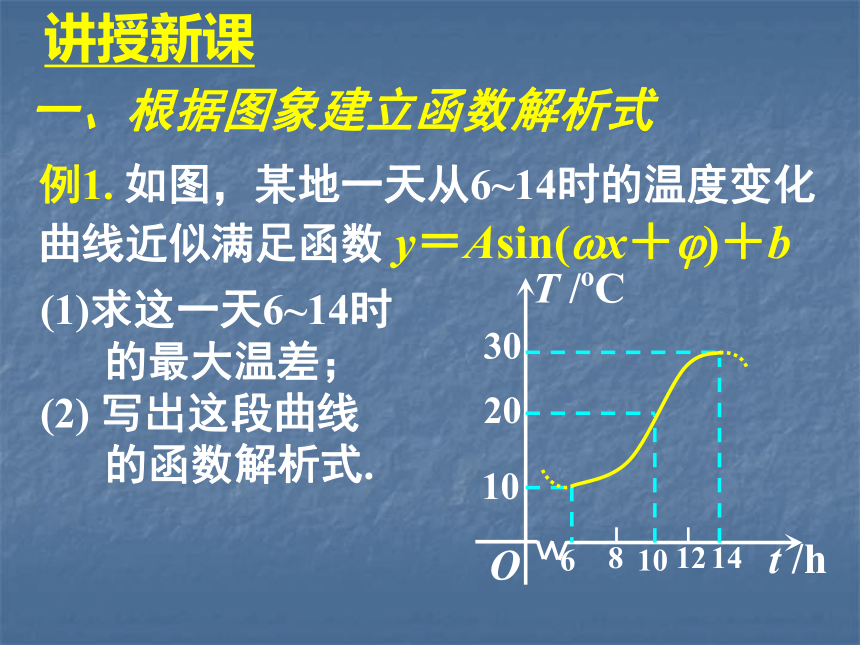
的简单应用讲授新课例1. 如图,某地一天从6~14时的温度变化
曲线近似满足函数 y=Asin(?x+?)+b求这一天6~14时
的最大温差;
(2) 写出这段曲线
的函数解析式.讲授新课例1. 如图,某地一天从6~14时的温度变化
曲线近似满足函数 y=Asin(?x+?)+b求这一天6~14时
的最大温差;
(2) 写出这段曲线
的函数解析式.一、根据图象建立函数解析式讲授新课一、根据图象建立函数解析式 小结:利用函数的模型(函数的
图象)解决问题,根据图象建立函数
解析式.例2. 画出函数y=|sinx|的图象并观察其
周期.讲授新课例2. 画出函数y=|sinx|的图象并观察其
周期.二、根据解析式模型建立图象模型讲授新课讲授新课例2. 画出函数y=|sinx|的图象并观察其
周期.二、根据解析式模型建立图象模型讲授新课 小结:利用函数解析式模型建立
函数图象模型,并根据图象认识性质.二、根据解析式模型建立图象模型例2. 画出函数y=|sinx|的图象并观察其
周期.讲授新课例3. 如图,设地球表面某地正午太阳高度角为?,?为此时太阳直射纬度,?为该地的纬度值,那么这三个量之间的关系是? =90o-|? -? |.当地夏半年?取正值,冬半年?取负值. 如果在北京地区(纬度数约为北纬40o)的一
幢高为h0的楼房北面盖一
新楼,要使新楼一层正午
的太阳全年不被前
面的楼房遮挡,两
楼的距离不应小于
多少?讲授新课例3. 如图,设地球表面某地正午太阳高度角为?,?为
此时太阳直射纬度,?为该地的纬度值,那么这三个
量之间的关系是? =90o-|? -? |.当地夏半年?取正值,
冬半年?取负值. 如果在北京地区(纬度数约为北纬40o)的一幢高为
h0的楼房北面盖一新楼,要使新楼一层正午的太阳全
年不被前面的楼房遮挡,两楼的距离不应小于多少?|?-|?太阳光? -??讲授新课例4. 下面是某港口在某季节每天的时间与水深
的关系表:选用一个函数来近似描述这个港口的水深
与时间的函数关系,并给出整点时的水深的
近似数值(精确到0.001).讲授新课问题1:观察上表的数据,你发现了
什么规律?讲授新课问题1:观察上表的数据,你发现了
什么规律?问题2:根据数据作出散点图. 观察图形,
你认为可以用怎样的函数模型刻
画其中的规律?讲授新课问题1:观察上表的数据,你发现了
什么规律?问题3:能根据函数模型求整点时的水深
吗?问题2:根据数据作出散点图. 观察图形,
你认为可以用怎样的函数模型刻
画其中的规律?讲授新课例4. 下面是某港口在某季节每天的时间与水深
的关系表:(2) 一条货船的吃水深度(船底与水面的距离)为
4米,安全条例规定至少要有1.5米的安全间隙
(船底与洋底的距离) ,该船何时能进入港口?
在港口能呆多久?讲授新课例4. 下面是某港口在某季节每天的时间与水深
的关系表:(3) 若某船的吃水深度为4米,安全间隙为1.5米,
该船在2:00开始卸货,吃水深度以每小时0.3米
的速度减少,那么该船在什么时间必须停止卸
货,将船驶向较深的水域?讲授新课 小结:你能概括出建立三角函数模型
解决实际问题的基本步骤吗?课堂小结1. 三角函数模型应用基本步骤:
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
(2)根据解析式作出图象;
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
(2)根据解析式作出图象;
(3)将实际问题抽象为与三角函数有关
的简单函数模型.
课堂小结1. 三角函数模型应用基本步骤:
(1)根据图象建立解析式;
(2)根据解析式作出图象;
(3)将实际问题抽象为与三角函数有关
的简单函数模型.
2. 利用收集到的数据作出散点图,并
根据散点图进行函数拟合,从而得到
函数模型.课后作业
