专题2.2匀变速直线运动的速度与时间的关系(课件)-2017-2018学年高一物理同步备课资源整合(二)
文档属性
| 名称 | 专题2.2匀变速直线运动的速度与时间的关系(课件)-2017-2018学年高一物理同步备课资源整合(二) |  | |
| 格式 | zip | ||
| 文件大小 | 564.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-11-06 13:06:00 | ||
图片预览






文档简介
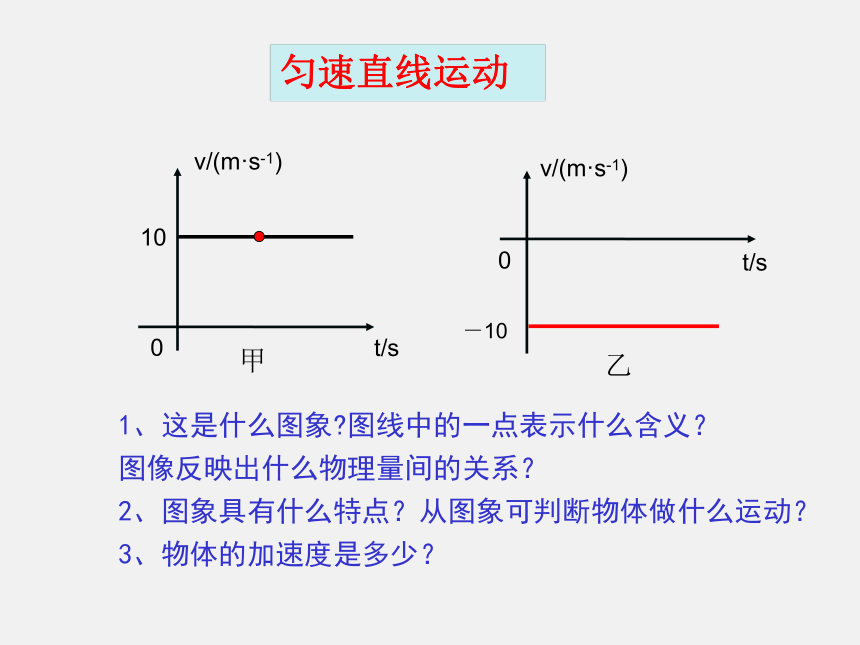
课件29张PPT。★重难点一:匀变速直线运动★1、这是什么图象?图线中的一点表示什么含义?
图像反映出什么物理量间的关系?
2、图象具有什么特点?从图象可判断物体做什么运动?
3、物体的加速度是多少?匀速直线运动1、从图可判断物体速度如何变化?
2、物体的加速度如何表示?又如何变化呢?
3、物体做什么运动?
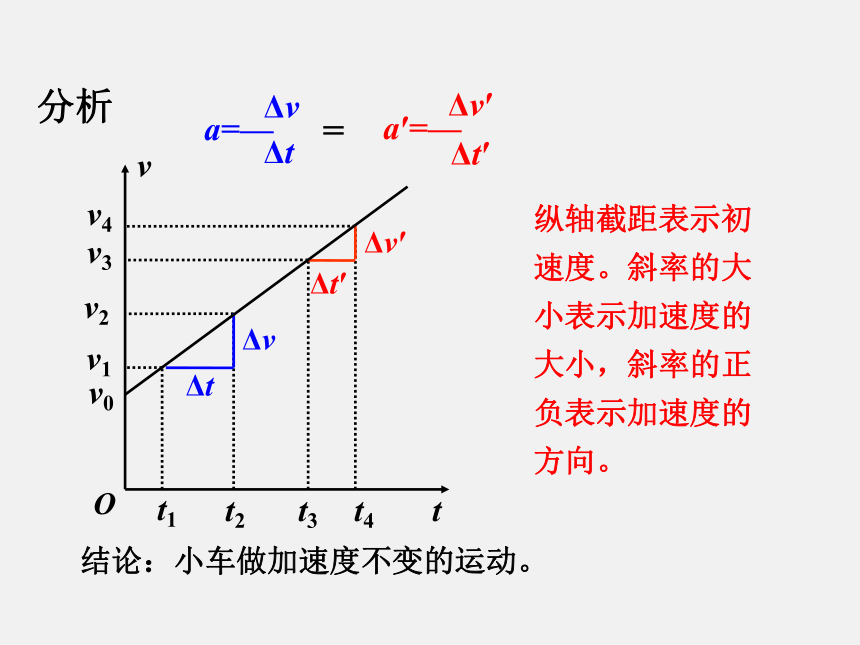
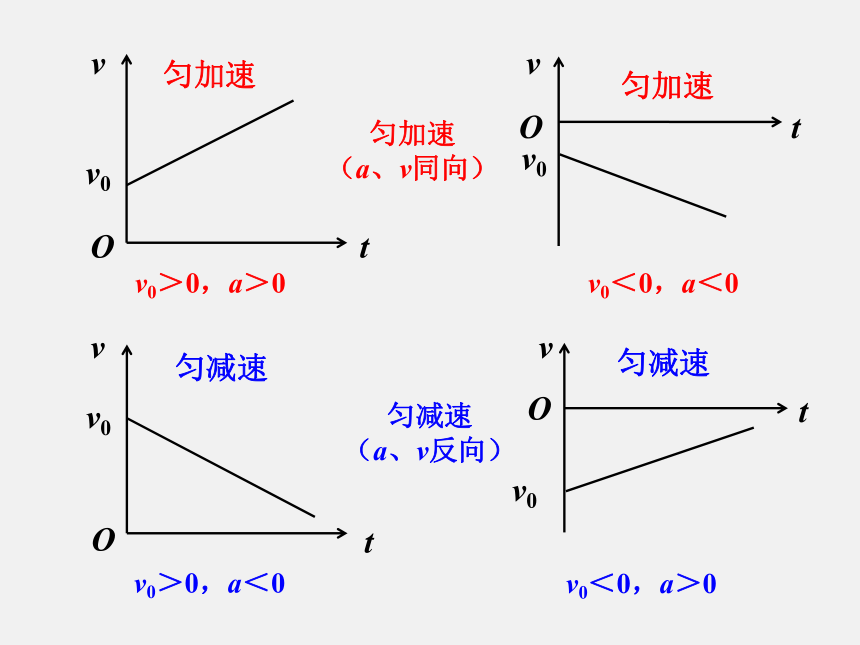
4、a>0一定是加速运动,a<0一定是减速运动吗?a>0Ott1t2vv0v1v2v3v4t4t3ΔvΔv?ΔtΔt?=结论:小车做加速度不变的运动。纵轴截距表示初速度。斜率的大小表示加速度的大小,斜率的正负表示加速度的方向。分析匀变速直线运动加速度不变变化量均匀增加均匀减小匀变速直线运动的v-t图象是一条倾斜的直线,如下图所示,直线a反映了速度随时间是的,即是匀加速直线运动的图象;直线b反映了速度随时间是的,即是匀减速直线运动的图象。匀变速直线运动的速度—时间图象v0>0,a>0v0<0,a<0匀加速
(a、v同向)匀减速
(a、v反向)v0<0,a>0v0>0,a<0匀加速匀加速匀减速匀减速Ovtv0v0vtOvtv0v0OOtv★重难点二:匀变速直线运动的速度与时间的关系式★at表示速度的变化量问
题1、在公式中,各物理量的意义是什么?2、在公式中,哪些物理量是矢量?3、利用公式计算时,对于矢量怎么处理?4、公式的适用范围是什么?v=v0+atOvtv0at初速度加速度对应时间末速度v01.速度公式:v=_______________。
2.对公式的理解:做匀变速直线运动的物体,在t时刻的速度v等于物体在开始时刻的_____________加上在整个过程中速度的______________。速度与时间的关系式v0+at速度v0变化量at1.公式v=v0+at的物理意义:对做匀变速直线运动的物体,描述其速度随时间的变化规律。
2.公式中各符号的含义
(1)v0、v分别表示物体的初、末速度。
(2)a为物体的加速度,且a为恒量。对速度公式的理解3.公式的矢量性
(1)公式中的v0、v、a为矢量,应用公式解题时,一般取v0的方向为正方向,a、v与v0的方向相同时取正值,与v0的方向相反时取负值。
(2)a与v0同向时物体做匀加速运动,a与v0方向相反时,物体做匀减速直线运动。
4.公式的适用条件:公式v=v0+at只适用于匀变速直线运动。
5.公式v=v0+at的特殊形式
(1)当a=0时,v=v0(匀速直线运动)
(2)当v0=0时,v=at(由静止开始的匀加速直线运动)对速度公式的理解【典型例题】甲、乙两物体分别做匀加速和匀减速直线运动,已知乙的初速度是甲的初速度的2.5倍,且甲的加速度大小是乙的加速度大小的2倍,经过4 s两者的速度均达到8 m/s,则两者的初速度大小分别为多大?两者加速度大小分别为多大?【答案】4 m/s; 10 m/s ; 1 m/s2 ; 0.5 m/s2【针对训练】独轮摩托车是一种新型交通工具。它通过内置的一对陀螺仪来实现平衡的。而它的速度则是由倾斜程度来控制的,想要加速则向前倾,减速和后退则向后倾。外教阿里骑着一款独轮摩托车从静止开始,以1.6 m/s2的加速度沿直线匀加速行驶了4 s,又以1.2 m/s2的加速度沿直线匀减速行驶了3 s,然后做匀速直线运动,
独轮摩托车做匀速直线运动的
速度大小为 。【答案】2.8 m/s★重难点三:速度图象(v-t)图象的理解及应用★2.匀变速直线运动的v-t图象
(1)如图乙所示,匀变速直线运动的v-t图象是一条倾斜的直线,直线a反映速度随时间是均匀增大的,为匀加速直线运动的图象;直线b反映速度随时间是均匀减小的,为匀减速直线运动的图象.
(2)若物体做匀减速直线运动,加速度为a,当速度减为零之后,又会反向做匀加速直线运动,如果加速度不变,则整个运动过程也是匀变速直线运动,如图乙中的c所示.【典型例题】物体从静止开始竖直向上运动,先以0.1m/s2 的加速度加速10s,紧接着匀速运动20s,
最后匀减速运动16s 停止。求:
(1)物体在减速过程中的加速度;
(2)画出物体的v-t 图像。【答案】A【解析】由图知:A的速度均匀增大,做匀加速直线运动,故A正确.B的速度沿负方向,而且均匀增大,所以沿负方向做匀加速直线运动,故B错误.根据图线的斜率表示加速度,可知A的加速度为正值,B的加速度为负值,由于B的斜率绝对值更大,所以B的加速度大于A的加速度.故C错误.速度是矢量,2s末物体A的速度大小为2m/s,B的速度大小为4m/s,所以A物体速度比物体B的速度小,D错误;故选A.点睛:本题是速度-时间图象问题,要知道速度-时间图象直接反映了瞬时速度随时间的变化情况,时间轴上方速度是正,时间轴下方速度是负;倾斜的直线表示物体做匀变速直线运动.图线的斜率表示加速度,加速度向右上方倾斜,加速度为正,向右下方倾斜加速度为负.比较速度和加速度的大小只比较绝对值即可.
图像反映出什么物理量间的关系?
2、图象具有什么特点?从图象可判断物体做什么运动?
3、物体的加速度是多少?匀速直线运动1、从图可判断物体速度如何变化?
2、物体的加速度如何表示?又如何变化呢?
3、物体做什么运动?
4、a>0一定是加速运动,a<0一定是减速运动吗?a>0Ott1t2vv0v1v2v3v4t4t3ΔvΔv?ΔtΔt?=结论:小车做加速度不变的运动。纵轴截距表示初速度。斜率的大小表示加速度的大小,斜率的正负表示加速度的方向。分析匀变速直线运动加速度不变变化量均匀增加均匀减小匀变速直线运动的v-t图象是一条倾斜的直线,如下图所示,直线a反映了速度随时间是的,即是匀加速直线运动的图象;直线b反映了速度随时间是的,即是匀减速直线运动的图象。匀变速直线运动的速度—时间图象v0>0,a>0v0<0,a<0匀加速
(a、v同向)匀减速
(a、v反向)v0<0,a>0v0>0,a<0匀加速匀加速匀减速匀减速Ovtv0v0vtOvtv0v0OOtv★重难点二:匀变速直线运动的速度与时间的关系式★at表示速度的变化量问
题1、在公式中,各物理量的意义是什么?2、在公式中,哪些物理量是矢量?3、利用公式计算时,对于矢量怎么处理?4、公式的适用范围是什么?v=v0+atOvtv0at初速度加速度对应时间末速度v01.速度公式:v=_______________。
2.对公式的理解:做匀变速直线运动的物体,在t时刻的速度v等于物体在开始时刻的_____________加上在整个过程中速度的______________。速度与时间的关系式v0+at速度v0变化量at1.公式v=v0+at的物理意义:对做匀变速直线运动的物体,描述其速度随时间的变化规律。
2.公式中各符号的含义
(1)v0、v分别表示物体的初、末速度。
(2)a为物体的加速度,且a为恒量。对速度公式的理解3.公式的矢量性
(1)公式中的v0、v、a为矢量,应用公式解题时,一般取v0的方向为正方向,a、v与v0的方向相同时取正值,与v0的方向相反时取负值。
(2)a与v0同向时物体做匀加速运动,a与v0方向相反时,物体做匀减速直线运动。
4.公式的适用条件:公式v=v0+at只适用于匀变速直线运动。
5.公式v=v0+at的特殊形式
(1)当a=0时,v=v0(匀速直线运动)
(2)当v0=0时,v=at(由静止开始的匀加速直线运动)对速度公式的理解【典型例题】甲、乙两物体分别做匀加速和匀减速直线运动,已知乙的初速度是甲的初速度的2.5倍,且甲的加速度大小是乙的加速度大小的2倍,经过4 s两者的速度均达到8 m/s,则两者的初速度大小分别为多大?两者加速度大小分别为多大?【答案】4 m/s; 10 m/s ; 1 m/s2 ; 0.5 m/s2【针对训练】独轮摩托车是一种新型交通工具。它通过内置的一对陀螺仪来实现平衡的。而它的速度则是由倾斜程度来控制的,想要加速则向前倾,减速和后退则向后倾。外教阿里骑着一款独轮摩托车从静止开始,以1.6 m/s2的加速度沿直线匀加速行驶了4 s,又以1.2 m/s2的加速度沿直线匀减速行驶了3 s,然后做匀速直线运动,
独轮摩托车做匀速直线运动的
速度大小为 。【答案】2.8 m/s★重难点三:速度图象(v-t)图象的理解及应用★2.匀变速直线运动的v-t图象
(1)如图乙所示,匀变速直线运动的v-t图象是一条倾斜的直线,直线a反映速度随时间是均匀增大的,为匀加速直线运动的图象;直线b反映速度随时间是均匀减小的,为匀减速直线运动的图象.
(2)若物体做匀减速直线运动,加速度为a,当速度减为零之后,又会反向做匀加速直线运动,如果加速度不变,则整个运动过程也是匀变速直线运动,如图乙中的c所示.【典型例题】物体从静止开始竖直向上运动,先以0.1m/s2 的加速度加速10s,紧接着匀速运动20s,
最后匀减速运动16s 停止。求:
(1)物体在减速过程中的加速度;
(2)画出物体的v-t 图像。【答案】A【解析】由图知:A的速度均匀增大,做匀加速直线运动,故A正确.B的速度沿负方向,而且均匀增大,所以沿负方向做匀加速直线运动,故B错误.根据图线的斜率表示加速度,可知A的加速度为正值,B的加速度为负值,由于B的斜率绝对值更大,所以B的加速度大于A的加速度.故C错误.速度是矢量,2s末物体A的速度大小为2m/s,B的速度大小为4m/s,所以A物体速度比物体B的速度小,D错误;故选A.点睛:本题是速度-时间图象问题,要知道速度-时间图象直接反映了瞬时速度随时间的变化情况,时间轴上方速度是正,时间轴下方速度是负;倾斜的直线表示物体做匀变速直线运动.图线的斜率表示加速度,加速度向右上方倾斜,加速度为正,向右下方倾斜加速度为负.比较速度和加速度的大小只比较绝对值即可.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
