北师大版八年级数学上册第一章 勾股定理特色题讲解教案
文档属性
| 名称 | 北师大版八年级数学上册第一章 勾股定理特色题讲解教案 |  | |
| 格式 | zip | ||
| 文件大小 | 241.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-06 22:19:06 | ||
图片预览



文档简介
第一次课《勾股定理》之特色题
一、清新扮靓的规律探究题
例1(成都市)如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,
再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积为1,按上述方法所作的正方形的面积依次为,…,(n为正整数),那么第8个正方形的面积
=_______.
【解析】:求解这类题目的常见策略是:“从特殊到一般”.
即是先通过观察几个特殊的数式中的变数与不变数,得出一
般规律,然后再利用其一般规律求解所要解决的问题.对于
此题,由勾股定理、正方形的面积计算公式易求得:
,
照此规律可知:,
观察数1、2、4、8、16易知:,于是可知
因此,
二、考查阅读理解能力的材料分析题
例2(临安)阅读下列题目的解题过程:
已知a、b、c为的三边,且满足,试判断的形状.
解:
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:
;
(2)错误的原因为:
(3)本题正确的结论为:
.
【解析】:材料阅读题是近年中考的热点命题,其类型多种多样,本题属于“判断纠错型”题目.集中考查了因式分解、勾股定理等知识.在由得到等式没有错,错在将这个等式两边同除了一个可能为零的式子.若,则有,从而得,这时,为等腰三角形.因此:
(1)选C.
(2)没有考虑
(3)
三、渗透新课程理念的图形拼接题
例3(长春)如图,在Rt△ABC中,∠C
=
90°,AC
=
4,BC
=
3.在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如图所示.
要求:在答题卡的两个备用图中分别画出两种与示例不同的拼接方法,并在图中标明拼接的直角三角形的三边长.(请同学们先用铅笔画现草图,确定后再用0.5毫米的黑色签字笔画出正确的图形)
示例图
备用图
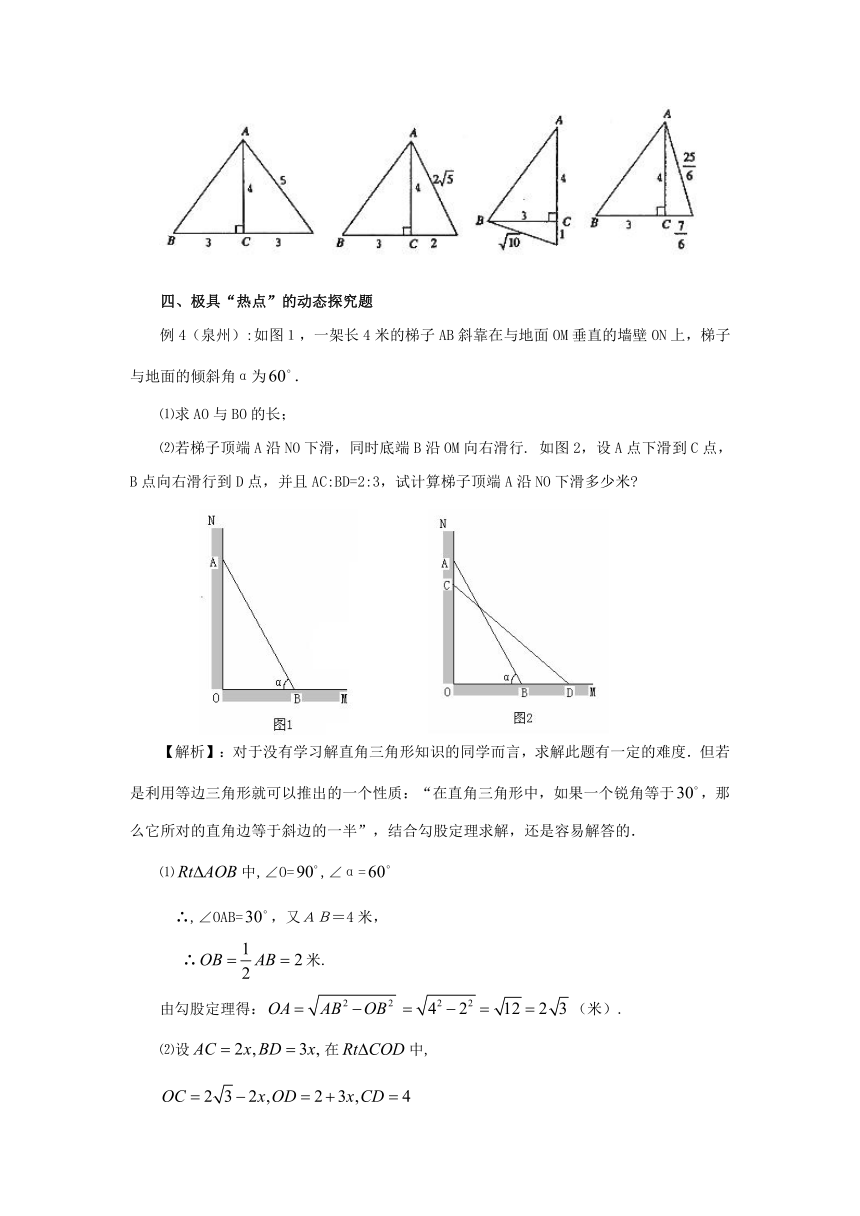
【解析】:要在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,关键是腰与底边的确定;要求在图中标明拼接的直角三角形的三边长,这需要用到勾股定理知识.下面四种拼接方法可供参考.
四、极具“热点”的动态探究题
例4(泉州):如图1,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为.
⑴求AO与BO的长;
⑵若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
如图2,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米
【解析】:对于没有学习解直角三角形知识的同学而言,求解此题有一定的难度.但若是利用等边三角形就可以推出的一个性质:“在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半”,结合勾股定理求解,还是容易解答的.
⑴中,∠O=,∠α=
∴,∠OAB=,又AB=4米,
∴米.
由勾股定理得:(米).
⑵设在中,
根据勾股定理:
∴
-
∴
∵ ∴
∴
所以,
AC=2x=
即梯子顶端A沿NO下滑了米.
勾股定理中的常见题型例析
勾股定理是几何计算中运用最多的一个知识点.考查的主要方式是将其综合到几何应用的解答题中,常见的题型有以下几种:
一、探究开放题
例1如图1,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…….
(1)记正方形ABCD的边长为=1,依上述方法所作的正方形的边长依次为,,,…,,求出,,的值.
(2)根据以上规律写出第n个正方形的边长的表达式.
分析:依次运用勾股定理求出a2,a3,a4,再观察、归纳出一般规律.
解:(1)∵四边形ABCD为正方形,∴AB=BC=CD=AD=1.
由勾股定理,得AC=,
同理,AE=2,EH=
.即
a2=
,a3=2,a4=
.
(2)
∵,
,
,
,
∴
.
点拨:探究开放题形式新颖、思考方向不确定,因此综合性和逻辑性较强,它着力于考查观察、分析、比较、归纳、推理等方面的能力,对提高同学们的思维品质和解决问题的能力具有十分重要的作用.
二、动手操作题
例2如图2,图(1)是用硬纸板做成的两个全等的直角三角形,两条直角边长分别为a和b,斜边长为c.图(2)是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图,写出它是什么图形;
(2)用这个图形证明勾股定理;
(3)假设图(1)中的直角三角形有苦干个,你能运用图(1)所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).
解:(1)所拼图形图3所示,它是一个直角梯形.
(2)由于这个梯形的两底分别为a、b,腰为(a+b),所以梯形的面积为.又因为这个梯形的面积等于三个直角三角形的面积和,所以梯形的面积又可表示为:.
∴.
∴.
(3)所拼图形如图4.
点拨:动手操作题内容丰富,解法灵活,有利于考查解题者的动手能力和创新设计的才能。本题通过巧妙构图,然后运用面积之间的关系来验证勾股定理。
三、阅读理解题
例3
已知a,b,c为△ABC的三边且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.小明同学是这样解答的.
解:∵a2c2-b2c2=a4-b4,
∴
∴.
订正:∴
△ABC是直角三角形
.
横线与问号是老师给他的批注,老师还写了如下评语:“你的解题思路很清晰,但解题过程中出现了错误,相信你再思考一下,一定能写出完整的解题过程.”请你帮助小明订正此题,好吗?
分析:这类阅读题在展现问题全貌的同时,在关键处留下疑问点,让同学们认真思考,以补充欠缺的部分,这相当于提示了整体思路,而让学生在整体理解的基础上给予具体的补缺.因此,本题可作如下订正:
解:∵a2c2-b2c2=a4-b4,
∴.
∴,∴或.
∴或.
∴
△ABC是等腰三角形或直角三角形
.
点拨:阅读理解题它与高考中兴起的信息迁移题有异曲同工之巧.解决的关键是抓住疑问点,补全漏洞.
四、方案设计题
例4给你一根长为30cm的木棒,现要你截成三段,做一个直角三角形,怎样截取(允许有余料)?请你设计三种方案.
分析:构造直角三角形,可根据勾股定理的逆定理来解决.
解:方案一:分别截取3cm,4cm,5cm;
方案二:分别截取6cm,8cm,10cm;
方案三:分别截取5cm,12cm,13cm.
点拨:本题首先依据勾股定理的逆定理进行分析,设计出方案,然后再通过测量、截取、加工等活动方能完成.既要思考,又要动手.让学生在这个过程中,体会做数学的快乐.
五、实际应用题
例5如图5,三个正方形形状的土地面积分别是74英亩、116英亩、370英亩,三个正方形恰好围着一个池塘.现要将这560英亩的土地拍卖,如果有人能计算出池塘的面积,则池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗?
分析:巴尔教授解决这个问题时首先发现三个正方形的面积74、116、370相当于池塘的三条边的平方,因而联想到勾股定理,得74=52+72,116=42+102,370=92+172.于是作出图6,运用勾股定理的逆定理,问题就得以解决.
解:∵74=52+72,∴AB是两直角边分别为5和7的直角三角形的斜边,作出这个直角三角形,得Rt△ABE.
同理,作Rt△BCF,其中BF=4,FC=10.延长AE、CF交于D,则AD=9,CD=17,而AC2=370=92+172=AD2+CD2,∴△ACD是直角三角形,∠ADC=90°.
∴=.
点拨:本题的关键是运用勾股定理和它的逆定理构造新图形,用构造法解题的思想,有助于提高运用数学知识解决实际问题的能力.
勾股定理的逆定理典例分析
例1
如果一个三角形的三边长分别为
,则这三角形是直角三角形
分析:
验证
三边是否符合勾股定量的逆定理
证明:∵
∴
∵∠C=
说明:勾股定理的逆定理给出了判定一个三角形是直角三角形的方法,与前面学习的方法不同,它需要通过代数运算算出来.
例2 已知:如图,四边形ABCD中,∠B=
,AB=3,BC=4,CD=12,AD=13求四边形ABCD的面积
分析:我们不知道这个四边形是否为特殊的四边形,所以将四边形分割为两个三角形,只要求出这两个三角形的面积,四边形的面积就等于这两个三角形的面积和.
解:连结AC
∵∠B=
,AB=3,BC=4
∴
∴AC=5
∵
∴
∴∠ACD=
说明:求四边形的面积问题转化为两个三角形的面积问题,在此利用勾股定理的逆定理判定三角形为直角三角形.
例3 如图,已知:CD⊥AB于D,且有
求证:△ACB为直角三角形
分析:根据勾股定理的逆定理,只需证
即可
证明:∵CD⊥AB
∴
又∵
∴
∴△ABC为直角三角形
说明:充分利用勾股定理及其逆定理.
一、清新扮靓的规律探究题
例1(成都市)如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,
再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积为1,按上述方法所作的正方形的面积依次为,…,(n为正整数),那么第8个正方形的面积
=_______.
【解析】:求解这类题目的常见策略是:“从特殊到一般”.
即是先通过观察几个特殊的数式中的变数与不变数,得出一
般规律,然后再利用其一般规律求解所要解决的问题.对于
此题,由勾股定理、正方形的面积计算公式易求得:
,
照此规律可知:,
观察数1、2、4、8、16易知:,于是可知
因此,
二、考查阅读理解能力的材料分析题
例2(临安)阅读下列题目的解题过程:
已知a、b、c为的三边,且满足,试判断的形状.
解:
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:
;
(2)错误的原因为:
(3)本题正确的结论为:
.
【解析】:材料阅读题是近年中考的热点命题,其类型多种多样,本题属于“判断纠错型”题目.集中考查了因式分解、勾股定理等知识.在由得到等式没有错,错在将这个等式两边同除了一个可能为零的式子.若,则有,从而得,这时,为等腰三角形.因此:
(1)选C.
(2)没有考虑
(3)
三、渗透新课程理念的图形拼接题
例3(长春)如图,在Rt△ABC中,∠C
=
90°,AC
=
4,BC
=
3.在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如图所示.
要求:在答题卡的两个备用图中分别画出两种与示例不同的拼接方法,并在图中标明拼接的直角三角形的三边长.(请同学们先用铅笔画现草图,确定后再用0.5毫米的黑色签字笔画出正确的图形)
示例图
备用图
【解析】:要在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,关键是腰与底边的确定;要求在图中标明拼接的直角三角形的三边长,这需要用到勾股定理知识.下面四种拼接方法可供参考.
四、极具“热点”的动态探究题
例4(泉州):如图1,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为.
⑴求AO与BO的长;
⑵若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
如图2,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米
【解析】:对于没有学习解直角三角形知识的同学而言,求解此题有一定的难度.但若是利用等边三角形就可以推出的一个性质:“在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半”,结合勾股定理求解,还是容易解答的.
⑴中,∠O=,∠α=
∴,∠OAB=,又AB=4米,
∴米.
由勾股定理得:(米).
⑵设在中,
根据勾股定理:
∴
-
∴
∵ ∴
∴
所以,
AC=2x=
即梯子顶端A沿NO下滑了米.
勾股定理中的常见题型例析
勾股定理是几何计算中运用最多的一个知识点.考查的主要方式是将其综合到几何应用的解答题中,常见的题型有以下几种:
一、探究开放题
例1如图1,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…….
(1)记正方形ABCD的边长为=1,依上述方法所作的正方形的边长依次为,,,…,,求出,,的值.
(2)根据以上规律写出第n个正方形的边长的表达式.
分析:依次运用勾股定理求出a2,a3,a4,再观察、归纳出一般规律.
解:(1)∵四边形ABCD为正方形,∴AB=BC=CD=AD=1.
由勾股定理,得AC=,
同理,AE=2,EH=
.即
a2=
,a3=2,a4=
.
(2)
∵,
,
,
,
∴
.
点拨:探究开放题形式新颖、思考方向不确定,因此综合性和逻辑性较强,它着力于考查观察、分析、比较、归纳、推理等方面的能力,对提高同学们的思维品质和解决问题的能力具有十分重要的作用.
二、动手操作题
例2如图2,图(1)是用硬纸板做成的两个全等的直角三角形,两条直角边长分别为a和b,斜边长为c.图(2)是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图,写出它是什么图形;
(2)用这个图形证明勾股定理;
(3)假设图(1)中的直角三角形有苦干个,你能运用图(1)所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).
解:(1)所拼图形图3所示,它是一个直角梯形.
(2)由于这个梯形的两底分别为a、b,腰为(a+b),所以梯形的面积为.又因为这个梯形的面积等于三个直角三角形的面积和,所以梯形的面积又可表示为:.
∴.
∴.
(3)所拼图形如图4.
点拨:动手操作题内容丰富,解法灵活,有利于考查解题者的动手能力和创新设计的才能。本题通过巧妙构图,然后运用面积之间的关系来验证勾股定理。
三、阅读理解题
例3
已知a,b,c为△ABC的三边且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.小明同学是这样解答的.
解:∵a2c2-b2c2=a4-b4,
∴
∴.
订正:∴
△ABC是直角三角形
.
横线与问号是老师给他的批注,老师还写了如下评语:“你的解题思路很清晰,但解题过程中出现了错误,相信你再思考一下,一定能写出完整的解题过程.”请你帮助小明订正此题,好吗?
分析:这类阅读题在展现问题全貌的同时,在关键处留下疑问点,让同学们认真思考,以补充欠缺的部分,这相当于提示了整体思路,而让学生在整体理解的基础上给予具体的补缺.因此,本题可作如下订正:
解:∵a2c2-b2c2=a4-b4,
∴.
∴,∴或.
∴或.
∴
△ABC是等腰三角形或直角三角形
.
点拨:阅读理解题它与高考中兴起的信息迁移题有异曲同工之巧.解决的关键是抓住疑问点,补全漏洞.
四、方案设计题
例4给你一根长为30cm的木棒,现要你截成三段,做一个直角三角形,怎样截取(允许有余料)?请你设计三种方案.
分析:构造直角三角形,可根据勾股定理的逆定理来解决.
解:方案一:分别截取3cm,4cm,5cm;
方案二:分别截取6cm,8cm,10cm;
方案三:分别截取5cm,12cm,13cm.
点拨:本题首先依据勾股定理的逆定理进行分析,设计出方案,然后再通过测量、截取、加工等活动方能完成.既要思考,又要动手.让学生在这个过程中,体会做数学的快乐.
五、实际应用题
例5如图5,三个正方形形状的土地面积分别是74英亩、116英亩、370英亩,三个正方形恰好围着一个池塘.现要将这560英亩的土地拍卖,如果有人能计算出池塘的面积,则池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗?
分析:巴尔教授解决这个问题时首先发现三个正方形的面积74、116、370相当于池塘的三条边的平方,因而联想到勾股定理,得74=52+72,116=42+102,370=92+172.于是作出图6,运用勾股定理的逆定理,问题就得以解决.
解:∵74=52+72,∴AB是两直角边分别为5和7的直角三角形的斜边,作出这个直角三角形,得Rt△ABE.
同理,作Rt△BCF,其中BF=4,FC=10.延长AE、CF交于D,则AD=9,CD=17,而AC2=370=92+172=AD2+CD2,∴△ACD是直角三角形,∠ADC=90°.
∴=.
点拨:本题的关键是运用勾股定理和它的逆定理构造新图形,用构造法解题的思想,有助于提高运用数学知识解决实际问题的能力.
勾股定理的逆定理典例分析
例1
如果一个三角形的三边长分别为
,则这三角形是直角三角形
分析:
验证
三边是否符合勾股定量的逆定理
证明:∵
∴
∵∠C=
说明:勾股定理的逆定理给出了判定一个三角形是直角三角形的方法,与前面学习的方法不同,它需要通过代数运算算出来.
例2 已知:如图,四边形ABCD中,∠B=
,AB=3,BC=4,CD=12,AD=13求四边形ABCD的面积
分析:我们不知道这个四边形是否为特殊的四边形,所以将四边形分割为两个三角形,只要求出这两个三角形的面积,四边形的面积就等于这两个三角形的面积和.
解:连结AC
∵∠B=
,AB=3,BC=4
∴
∴AC=5
∵
∴
∴∠ACD=
说明:求四边形的面积问题转化为两个三角形的面积问题,在此利用勾股定理的逆定理判定三角形为直角三角形.
例3 如图,已知:CD⊥AB于D,且有
求证:△ACB为直角三角形
分析:根据勾股定理的逆定理,只需证
即可
证明:∵CD⊥AB
∴
又∵
∴
∴△ABC为直角三角形
说明:充分利用勾股定理及其逆定理.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
