第六章反比例函数复习课 课件

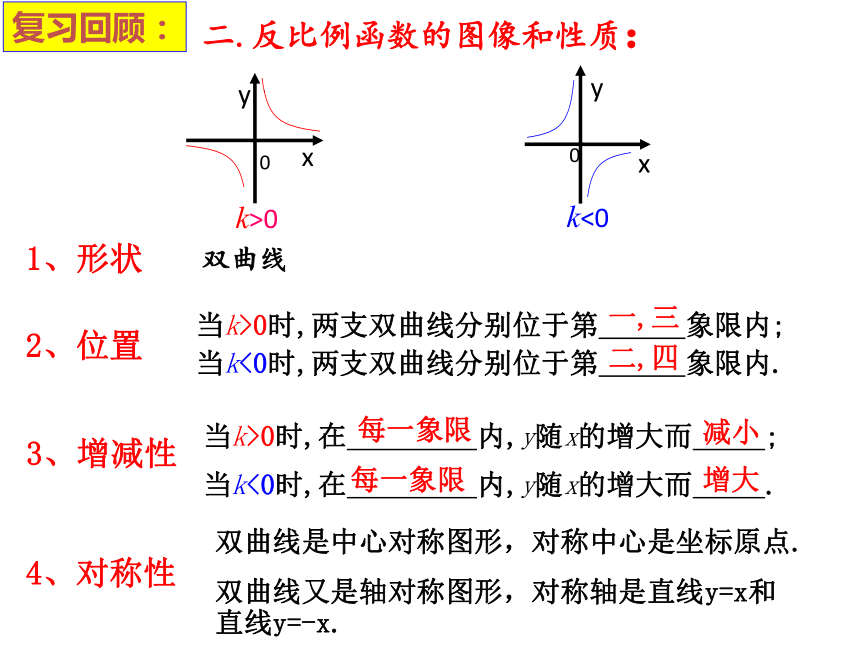
课件19张PPT。义务教育教科书（北师大版）数学 九年级上册一.反比例函数概念一般地，如果两个变量x，y之间的关系可以表示为 (其中k是不为0的常数)，那么称y是x的反比例函数.2、反比例函数解析式 3、自变量取值范围是x≠0的一切实数1、定义复习回顾：A、1个B、2个C、3个D、4个D -11、若函数 是反比例函数，则m = .同步练习：二.反比例函数的图像和性质：当k>0时,两支双曲线分别位于第 象限内;
当k<0时,两支双曲线分别位于第 象限内.当k>0时,在 内,y随x的增大而 ;
当k<0时,在 内,y随x的增大而 .复习回顾：1、形状双曲线2、位置3、增减性一,三减小每一象限二,四每一象限增大4、对称性双曲线是中心对称图形，对称中心是坐标原点.双曲线又是轴对称图形，对称轴是直线y=x和
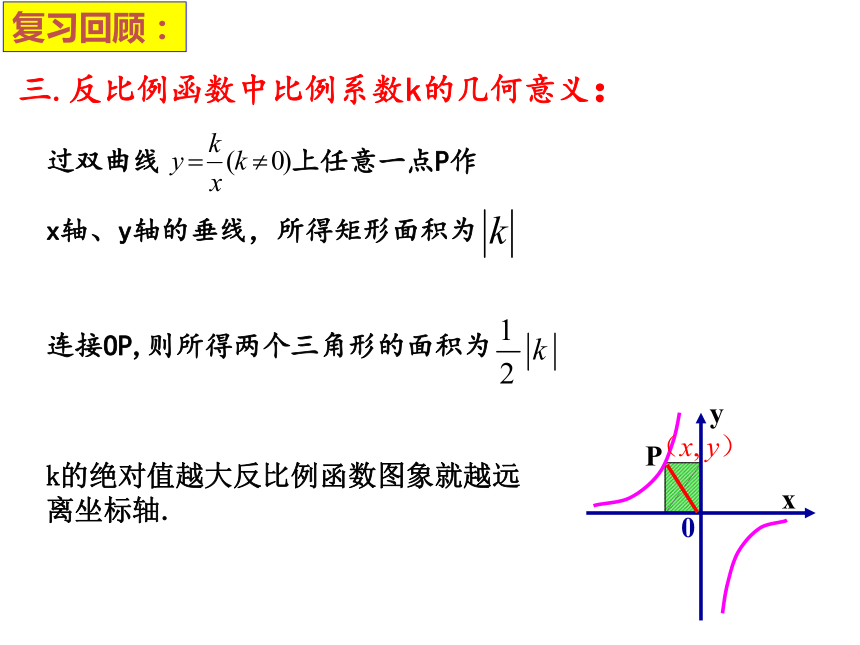
直线y=-x. 同步练习：A复习回顾：三.反比例函数中比例系数k的几何意义：过双曲线 上任意一点P作
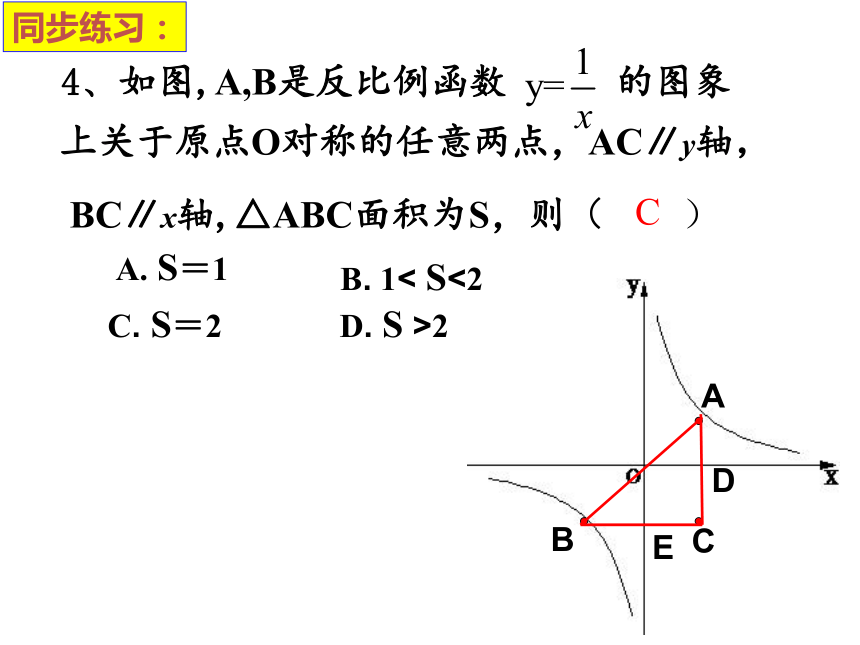
x轴、y轴的垂线，所得矩形面积为连接OP,则所得两个三角形的面积为k的绝对值越大反比例函数图象就越远离坐标轴.上关于原点O对称的任意两点，AC∥y轴，BC∥x轴,△ABC面积为S，则（ ）A. S＝1B. 1< S<2C. S＝2D. S >2ABCC4、如图,A,B是反比例函数 的图象同步练习：DE（x>0)1.5同步练习：6、如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（　　）．A、x＜－1　　　　　 B、x＞2
C、－1＜x＜0或x＞2　 D、x＜－1或0＜x＜2D复习回顾：四.反比例函数的应用：反比例函数与一次函数的综合7、函数y=k(x-1)的图象向下平移一个单位后与反比例
函数y=2/x的图象的交点为A,B,若点A的坐标为(2,1),
则点B的坐标为 .复习回顾：四.反比例函数的应用：反比例函数与一次函数的综合8、如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数
y= (x＞0)的图象上，则点E的坐标是( 　 ，　 ).复习回顾：四.反比例函数的应用：反比例函数与特殊平行四边形的综合9、如图所示，已知菱形OABC，点C在x轴上，直线y=x经过点A，
菱形OABC的面积是 .若反比例函数的图象经过点B，求k的值. 复习回顾：四.反比例函数的应用：反比例函数与特殊平行四边形的综合解：如图，过点A作AD⊥OC于D，设菱形的边长为a，∵直线y=x经过点A，
∴AD=OD= a，
∴菱形OABC面积=a? a=√2，解得a=∴AD=OD=1，∴点B的坐标为（ +1，1），解得k= +1，10、病人按规定的剂量服用某种药物，测得服药后
2小时，每毫升血液中的含药量达到最大值为 4 毫克．
已知服药后，2 小时前每毫升血液中的含药量 y(单位：
毫克)与时间 x(单位：小时)成正比例；2 小时后 y 与 x 成反比例(如图 26-7) ．根据以上信息解答下列问题：
(1)求当 0≤x≤2 时，y 与 x 的函数关系式；
(2)求当 x>2 时，y 与 x 的函数关系式；(3)若每毫升血液中的含药量
不低于 2毫克时治疗有效，
则服药一次，治疗疾病的
有效时间是多长？复习回顾：四.反比例函数的应用：反比例函数与实际问题的综合解：(1)当 0≤x≤2 时，y 与 x 成正比例函数关系．
设 y＝kx，由于点(2,4)在直线上，
所以 4＝2k，k＝2，即 y＝2x.
(2)当 x＞2 时，y 与 x 成反比例函数关系．
设 y＝k/x，由于点(2,4)反比例函数的图象上，
所以 k＝2×4＝8，即 y＝8/x.
(3)当 0≤x≤2 时，含药量不低于 2 毫克，
即 2x≥2，x≥1.即服药 1 小时后；
当 x>2 时，含药量不低于 2 毫克，所以服药一次，治疗疾病的有效时间是
1＋2＝3(小时)．忽略自变量的取值范围．体会.分享说出你这节课的收获和体验让大家与你分享吗？归纳总结：作业:
练习册部分11、已知：如图，反比例函数 的图象与一次函数y＝x+b的
图象交于点A（1,4）、点B（-4，n）.
（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积.拓展提升题：解(1) ∵A（1,4）在y= ，y=x+b上，
∴4= , 4=1+b， ∴k=4,b=3，
∴一次函数的解析式为y=x+3，反比例函数的解析式为y=4x；(2)∵点B在y=x+3上，∴n=-4+3 =-1，
∴点B的坐标为（-4，-1），
设y=x+3与y轴交于点C（0，y），
令x=0，则y=3，
∴点C的坐标为（0,3），∴OC=3，
如解图，过点A、B分别作y轴垂线
AE、BF，交y轴于E、F点，
由A（1,4），B（-4，-1）
可知AE=1，BF=4， 亲爱的同学们，当你为生活、学习的山重水复而愁眉苦脸时，不妨换一种方法看问题，或许，你会收获一个柳暗花明的美好心情.希望各位在今后的学习中，能善于发现，勇于探索，敢于创新！教师寄语