13.3.1 等腰三角形 课件(共26张PPT)
文档属性
| 名称 | 13.3.1 等腰三角形 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 724.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-07 00:00:00 | ||
图片预览





文档简介
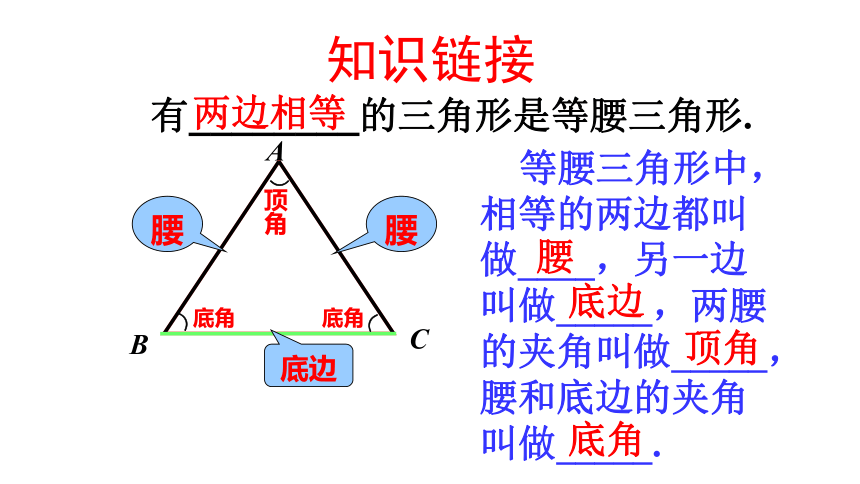
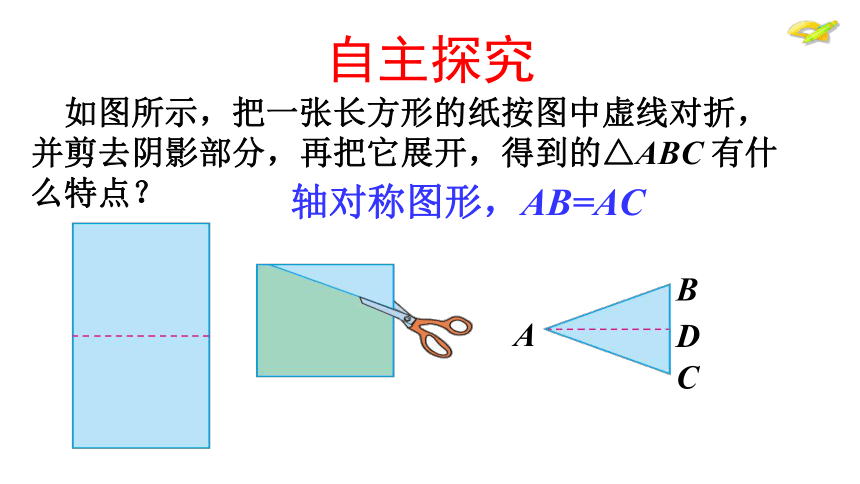
课件26张PPT。13.3.1 等腰三角形 等腰三角形中,相等的两边都叫做____,另一边叫做_____,两腰的夹角叫做_____,腰和底边的夹角叫做_____.底边有________的三角形是等腰三角形.知识链接两边相等腰底边顶角底角 如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?轴对称图形,AB=AC自主探究生活中的应用生活中的应用 只要铅锤线过等腰直角三角板底边的中点,就说明平面是水平的。你知道其中的道理吗? AB=AC BD=CD AD=AD ∠B = ∠C∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外,你还能发现它的其他特征吗?探究:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.1.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合. =90°已知:△ABC中,AB=AC.求证:∠B=?C.分析: 1.如何证明两个角相等? 2.如何构造两个全等的三角形? 提升:化归(转化)思想求证:等腰三角形的两个底角相等.GZJ合作探究等腰三角形的性质
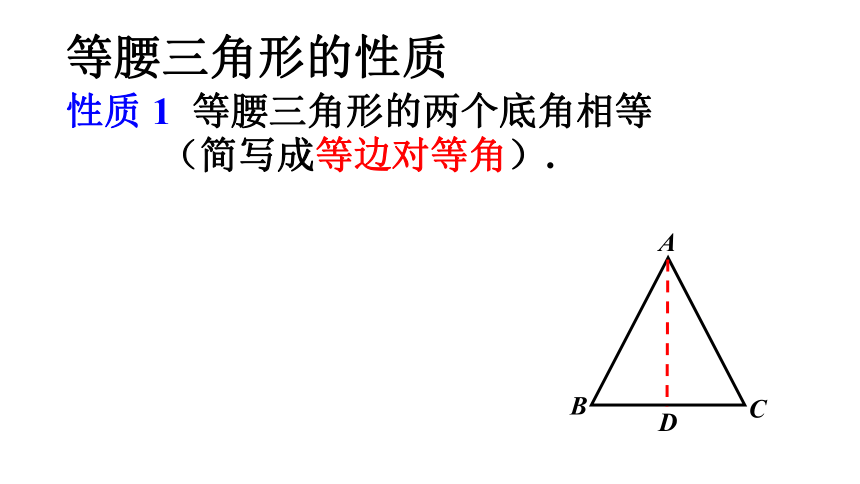
性质 1 等腰三角形的两个底角相等
(简写成等边对等角).成立吗?
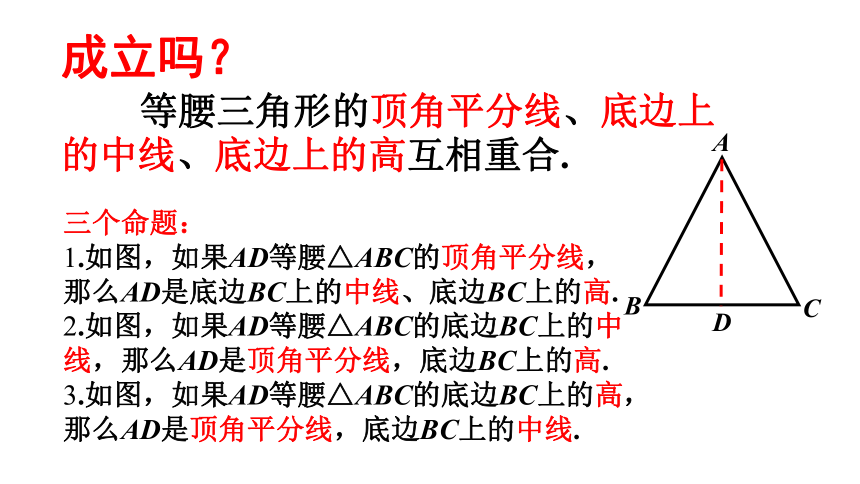
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.三个命题:
1.如图,如果AD等腰△ABC的顶角平分线,
那么AD是底边BC上的中线、底边BC上的高.
2.如图,如果AD等腰△ABC的底边BC上的中
线,那么AD是顶角平分线,底边BC上的高.
3.如图,如果AD等腰△ABC的底边BC上的高,
那么AD是顶角平分线,底边BC上的中线.等腰三角形的性质
性质 1 等腰三角形的两个底角相等
(简写成等边对等角).
等腰三角形的顶角平分线、
底边上的中线、底边上的高
互相重合性质 2 (简写成三线合一).D如图,作△ABC的中线AD. D如图, 作△ABC
的高AD.D如图,作顶角的平分线AD.等腰三角形常见辅助线归纳总结生活中的应用 只要铅锤线所在的直线过等腰直角三角板底边的中点,就说明平面是水平的。你知道其中的道理吗? 1. 在△ABC中, ∵ AB=AC
∴ ________= ________.
2. ( 1 ) ∵ AB=AC,AD是角平分线,
∴______⊥______,_______=______ ;
( 2 ) ∵ AB=AC ,AD是中线,
∴ ⊥ ,∠ = ∠____;
( 3 ) ∵ AB=AC ,AD⊥BC,
∴∠_____=∠_____,____=____.符号语言:∠B ∠CAD BC BD CD AD BC BADCAD BADCAD BD CD 内化提升:性质性质讨论内容:例1、例2、例3.
讨论方式:同桌讨论并订正.
讨论任务:订正学案.
讨论时间:5分钟左右.
合作讨论 例1. 在△ABC中,AB=AC,∠B=80°,∠C=_____,∠A=_____.
变式1:等腰三角形中,若一个角为80°,则它的另外两个角为___________________.
变式2:等腰三角形中,若一个角为120°,则它的另外两个角为________.80°80°,20°或50°,50°30°,30°20°合作探究考查知识点:等腰三角形的性质1.方法提升:如无特别说明,注意分类讨论.例2. 在△ABC中,AB=AC,AD为BC边上的中线,若∠BAD=20°,则∠ABC=_____.70°合作探究考查知识点:
等腰三角形的性质1、2.方法提升:
画出图形,数形结合.合作探究考查知识点:
等腰三角形的性质1.方法提升:
设出未知数,建立方程.例3. 如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD,求△ABC各内角的度数.当堂检测1.已知,在△ABC中,AB=AC,S△ABC=12cm2,
AD是△ABC的角平分线,AD=4cm,则BD的长为( )
A. 6cm B.4cm C. 3cm D.5cm
2.如图,在△ABC中,AB=AD=DC,∠BAD=26°,
求∠B和∠C的度数. 第1题图 第2题图 C收 获等腰三角形添加
辅助线的方法交流 收获等腰三角形
性质1等腰三角形
性质2转化、分类讨论
方程、数形结合
必做: 习题13.3 第1、4、7题
选做: 习题13.3 第6题分层作业 敬请批评指正!感悟数学,快乐生活.则∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作BC边上 的高ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C 方法一则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C 方法二则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C 方法三解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°.例3.如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?2.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.解:∵AB=AD=DC
∴ ∠B= ∠ADB,∠C= ∠DAC
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x
在△ABC中,
∠B+ ∠C+ ∠BAD+ ∠DAC
=2x+x+26°+x=180°
解得:x=38.5°,
∴ ∠B=77°, ∠C= 38.5°.课本第77页练习第3题
2.等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合. =90°已知:△ABC中,AB=AC.求证:∠B=?C.分析: 1.如何证明两个角相等? 2.如何构造两个全等的三角形? 提升:化归(转化)思想求证:等腰三角形的两个底角相等.GZJ合作探究等腰三角形的性质
性质 1 等腰三角形的两个底角相等
(简写成等边对等角).成立吗?
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.三个命题:
1.如图,如果AD等腰△ABC的顶角平分线,
那么AD是底边BC上的中线、底边BC上的高.
2.如图,如果AD等腰△ABC的底边BC上的中
线,那么AD是顶角平分线,底边BC上的高.
3.如图,如果AD等腰△ABC的底边BC上的高,
那么AD是顶角平分线,底边BC上的中线.等腰三角形的性质
性质 1 等腰三角形的两个底角相等
(简写成等边对等角).
等腰三角形的顶角平分线、
底边上的中线、底边上的高
互相重合性质 2 (简写成三线合一).D如图,作△ABC的中线AD. D如图, 作△ABC
的高AD.D如图,作顶角的平分线AD.等腰三角形常见辅助线归纳总结生活中的应用 只要铅锤线所在的直线过等腰直角三角板底边的中点,就说明平面是水平的。你知道其中的道理吗? 1. 在△ABC中, ∵ AB=AC
∴ ________= ________.
2. ( 1 ) ∵ AB=AC,AD是角平分线,
∴______⊥______,_______=______ ;
( 2 ) ∵ AB=AC ,AD是中线,
∴ ⊥ ,∠ = ∠____;
( 3 ) ∵ AB=AC ,AD⊥BC,
∴∠_____=∠_____,____=____.符号语言:∠B ∠CAD BC BD CD AD BC BADCAD BADCAD BD CD 内化提升:性质性质讨论内容:例1、例2、例3.
讨论方式:同桌讨论并订正.
讨论任务:订正学案.
讨论时间:5分钟左右.
合作讨论 例1. 在△ABC中,AB=AC,∠B=80°,∠C=_____,∠A=_____.
变式1:等腰三角形中,若一个角为80°,则它的另外两个角为___________________.
变式2:等腰三角形中,若一个角为120°,则它的另外两个角为________.80°80°,20°或50°,50°30°,30°20°合作探究考查知识点:等腰三角形的性质1.方法提升:如无特别说明,注意分类讨论.例2. 在△ABC中,AB=AC,AD为BC边上的中线,若∠BAD=20°,则∠ABC=_____.70°合作探究考查知识点:
等腰三角形的性质1、2.方法提升:
画出图形,数形结合.合作探究考查知识点:
等腰三角形的性质1.方法提升:
设出未知数,建立方程.例3. 如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD,求△ABC各内角的度数.当堂检测1.已知,在△ABC中,AB=AC,S△ABC=12cm2,
AD是△ABC的角平分线,AD=4cm,则BD的长为( )
A. 6cm B.4cm C. 3cm D.5cm
2.如图,在△ABC中,AB=AD=DC,∠BAD=26°,
求∠B和∠C的度数. 第1题图 第2题图 C收 获等腰三角形添加
辅助线的方法交流 收获等腰三角形
性质1等腰三角形
性质2转化、分类讨论
方程、数形结合
必做: 习题13.3 第1、4、7题
选做: 习题13.3 第6题分层作业 敬请批评指正!感悟数学,快乐生活.则∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作BC边上 的高ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C 方法一则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C 方法二则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C 方法三解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°.例3.如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?2.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.解:∵AB=AD=DC
∴ ∠B= ∠ADB,∠C= ∠DAC
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x
在△ABC中,
∠B+ ∠C+ ∠BAD+ ∠DAC
=2x+x+26°+x=180°
解得:x=38.5°,
∴ ∠B=77°, ∠C= 38.5°.课本第77页练习第3题
