2017-2018年甘肃省临洮县康家集初中八年级数学上册人教版课件:13.4最短路径问题 (共18张PPT)
文档属性
| 名称 | 2017-2018年甘肃省临洮县康家集初中八年级数学上册人教版课件:13.4最短路径问题 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1016.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-07 23:25:25 | ||
图片预览





文档简介
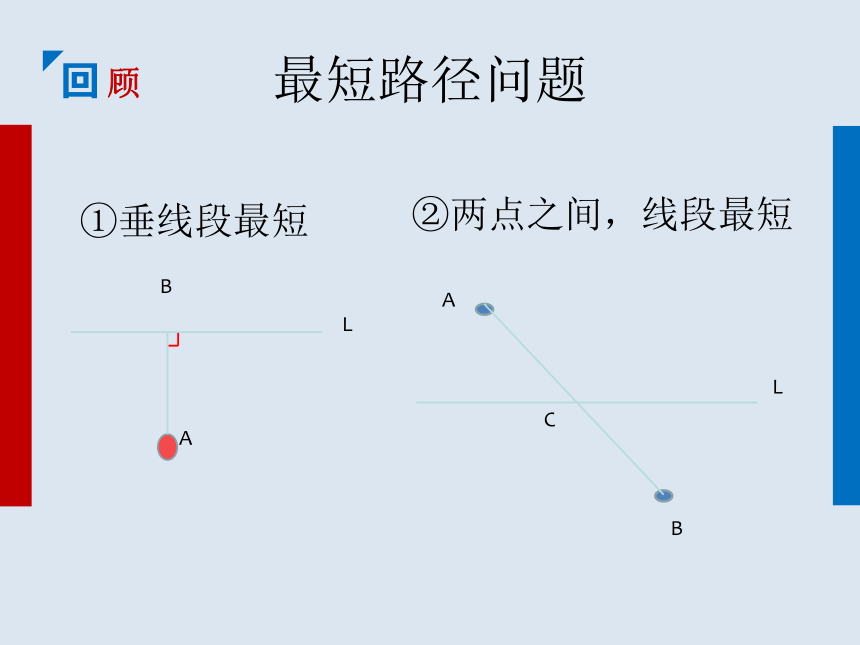
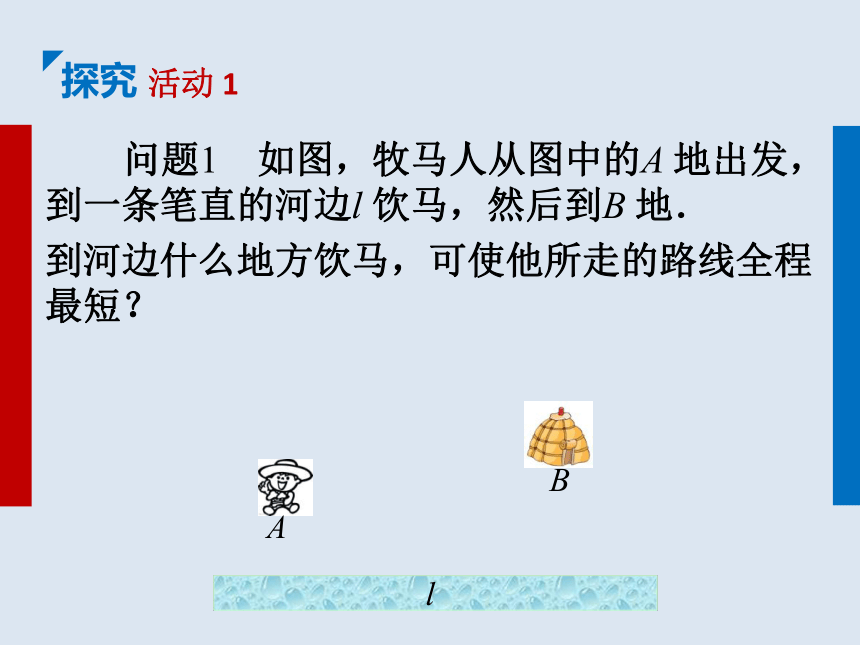
课件18张PPT。13.4 最短路径问题回顾最短路径问题①垂线段最短②两点之间,线段最短探究活动 1 问题1 如图,牧马人从图中的A 地出发,到一条笔直的河边l 饮马,然后到B 地.
到河边什么地方饮马,可使他所走的路线全程最短?探究活动 1追问1 这是一个实际问题,我们需要对实际问题怎么转化呢? 将A,B 两地抽象为两个点,将河l 抽象为一条直线. 上面的问题就转化为:当点C 在l 的什么位置时,AC 与CB 的和最小(如图).探究活动 1 追问1 对于问题2,如何
将点B“移”到l 的另一侧B′
处,满足直线l 上的任意一点
C,都保持CB 与CB′的长度
相等? 如图,点A,B 在直线l 的同侧,点C 是直线上的一个动点,当点C 在l 的什么位置时,AC 与CB
的和最小? 探究活动 1 追问2 你能利用轴对称的
有关知识,找到上问中符合条
件的点B′吗? 问题2 如图,点A,B 在直线l 的同侧,点C 是直
线上的一个动点,当点C 在l 的什么位置时,AC 与CB
的和最小? 探究活动 1 作法:
(1)作点B 关于直线l 的对称
点B′;
(2)连接AB′,与直线l 相交
于点C.
则点C 即为所求. 问题2 如图,点A,B 在直线l 的同侧,点C 是直
线上的一个动点,当点C 在l 的什么位置时,AC 与CB
的和最小? 探究活动 1 证明:如图,在直线l 上任取一点C'(与点C 不
重合),连接AC′,BC′,B'C'.
由轴对称的性质知,
BC =B'C,BC′=B'C'.
∴ AC +BC= AC +B′C = AB′,
AC′+BC′= AC′+B′C′. 问题3 你能用所学的知识证明AC +BC最短吗? 在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.探究活动 1 若直线l 上任意一点(与点
C 不重合)与A,B 两点的距离
和都大于AC +BC,就说明AC +
BC 最小. 证明AC +BC 最短时,为什么要在直线l 上任取一点C′(与点C 不重合),证明AC +BC <AC′
+BC′?这里的“C′”的作用是什么? 探究活动2
如图:牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
探究活动 2
如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
作法:1.作点C关于直线
OA 的 对称点点F,
2. 作点D关于直线 OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H,
则CG+GH+DH最短
FAOBD ·· CGHE探究活动 2
证明:在直线OA 上另外任取一点G,连接各点
∵点F,点C关于直线OA对称,点G.M在OA上,∴GF=GC,FM=CM,
同理HD=HE,ND=NE,
∴CM+MN+ND= FM+MN+NE= FE
CG+GH+HD=FG+GH+HE
在四边形EFGH中,
∵FG+GH+HE>FE(两点之间,线段最短)
即CG+GH+HD>CM+MN+ND
即CM+MN+ND最短
探究活动 2A/B/PQ探究活动 3 (造桥选址问题)如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直。)探究活动 3作法:
1.将点A沿垂直与河岸的
方向平移一个河宽到A‘
2.连接A’B交河对岸与点N,
则点N为建桥的位置,
MN为所建的桥。
ABMNabA′探究活动 3
证明:由平移的性质,得 AM∥A’N 且AM=A’N,
MN=M'N', AM’∥A’N’, AM’=A’N’,
所以A.B两地的距离:
AM+MN+BN=A’N+MN+BN=A’B+MN
若桥的位置建在M’N’处,
连接AC.CD.DB.CE,
则AB两地的距离为:
AM’+M’N’+N’B=A’N’+M’N’+N’B
=A’N’+N’B+MN
在△A’BN'中,∵A’N’+N’B>A’B
∴A’N’+N’B+MN>A’B+MN
即AM’+M’N’+N’B >AM+MN+BN
所以桥的位置建在MN处,AB两地的路程最短。
课堂练习 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数为多少? ABDCA′A″NMThanks
到河边什么地方饮马,可使他所走的路线全程最短?探究活动 1追问1 这是一个实际问题,我们需要对实际问题怎么转化呢? 将A,B 两地抽象为两个点,将河l 抽象为一条直线. 上面的问题就转化为:当点C 在l 的什么位置时,AC 与CB 的和最小(如图).探究活动 1 追问1 对于问题2,如何
将点B“移”到l 的另一侧B′
处,满足直线l 上的任意一点
C,都保持CB 与CB′的长度
相等? 如图,点A,B 在直线l 的同侧,点C 是直线上的一个动点,当点C 在l 的什么位置时,AC 与CB
的和最小? 探究活动 1 追问2 你能利用轴对称的
有关知识,找到上问中符合条
件的点B′吗? 问题2 如图,点A,B 在直线l 的同侧,点C 是直
线上的一个动点,当点C 在l 的什么位置时,AC 与CB
的和最小? 探究活动 1 作法:
(1)作点B 关于直线l 的对称
点B′;
(2)连接AB′,与直线l 相交
于点C.
则点C 即为所求. 问题2 如图,点A,B 在直线l 的同侧,点C 是直
线上的一个动点,当点C 在l 的什么位置时,AC 与CB
的和最小? 探究活动 1 证明:如图,在直线l 上任取一点C'(与点C 不
重合),连接AC′,BC′,B'C'.
由轴对称的性质知,
BC =B'C,BC′=B'C'.
∴ AC +BC= AC +B′C = AB′,
AC′+BC′= AC′+B′C′. 问题3 你能用所学的知识证明AC +BC最短吗? 在△AB′C′中,
AB′<AC′+B′C′,
∴ AC +BC<AC′+BC′.
即 AC +BC 最短.探究活动 1 若直线l 上任意一点(与点
C 不重合)与A,B 两点的距离
和都大于AC +BC,就说明AC +
BC 最小. 证明AC +BC 最短时,为什么要在直线l 上任取一点C′(与点C 不重合),证明AC +BC <AC′
+BC′?这里的“C′”的作用是什么? 探究活动2
如图:牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
探究活动 2
如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
作法:1.作点C关于直线
OA 的 对称点点F,
2. 作点D关于直线 OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H,
则CG+GH+DH最短
FAOBD ·· CGHE探究活动 2
证明:在直线OA 上另外任取一点G,连接各点
∵点F,点C关于直线OA对称,点G.M在OA上,∴GF=GC,FM=CM,
同理HD=HE,ND=NE,
∴CM+MN+ND= FM+MN+NE= FE
CG+GH+HD=FG+GH+HE
在四边形EFGH中,
∵FG+GH+HE>FE(两点之间,线段最短)
即CG+GH+HD>CM+MN+ND
即CM+MN+ND最短
探究活动 2A/B/PQ探究活动 3 (造桥选址问题)如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直。)探究活动 3作法:
1.将点A沿垂直与河岸的
方向平移一个河宽到A‘
2.连接A’B交河对岸与点N,
则点N为建桥的位置,
MN为所建的桥。
ABMNabA′探究活动 3
证明:由平移的性质,得 AM∥A’N 且AM=A’N,
MN=M'N', AM’∥A’N’, AM’=A’N’,
所以A.B两地的距离:
AM+MN+BN=A’N+MN+BN=A’B+MN
若桥的位置建在M’N’处,
连接AC.CD.DB.CE,
则AB两地的距离为:
AM’+M’N’+N’B=A’N’+M’N’+N’B
=A’N’+N’B+MN
在△A’BN'中,∵A’N’+N’B>A’B
∴A’N’+N’B+MN>A’B+MN
即AM’+M’N’+N’B >AM+MN+BN
所以桥的位置建在MN处,AB两地的路程最短。
课堂练习 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数为多少? ABDCA′A″NMThanks
