人教A版高中数学选修2-1课件:2.4.1抛物线及其标准方程 (共26张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-1课件:2.4.1抛物线及其标准方程 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 247.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-09 00:00:00 | ||
图片预览





文档简介
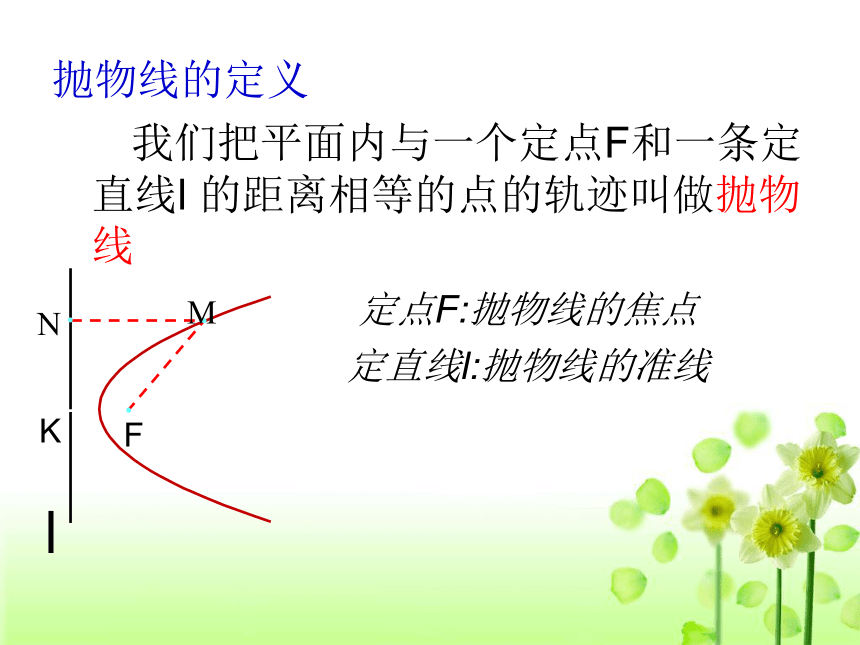
课件26张PPT。2.4.1抛物线及其标准方程 2.4 抛物线抛物线的定义 我们把平面内与一个定点F和一条定直线l 的距离相等的点的轨迹叫做抛物线
定点F:抛物线的焦点
定直线l:抛物线的准线
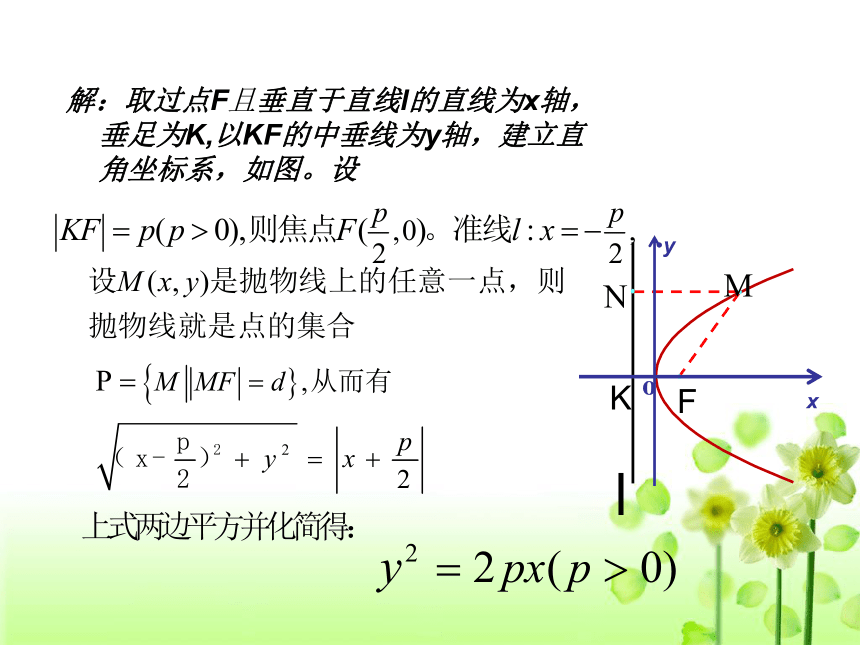
解:取过点F且垂直于直线l的直线为x轴,垂足为K,以KF的中垂线为y轴,建立直角坐标系,如图。设
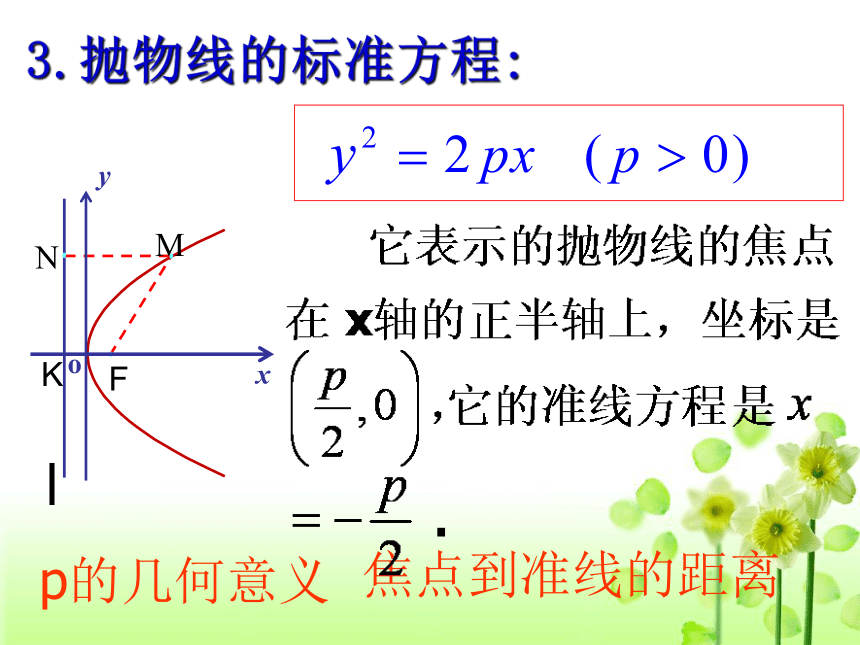
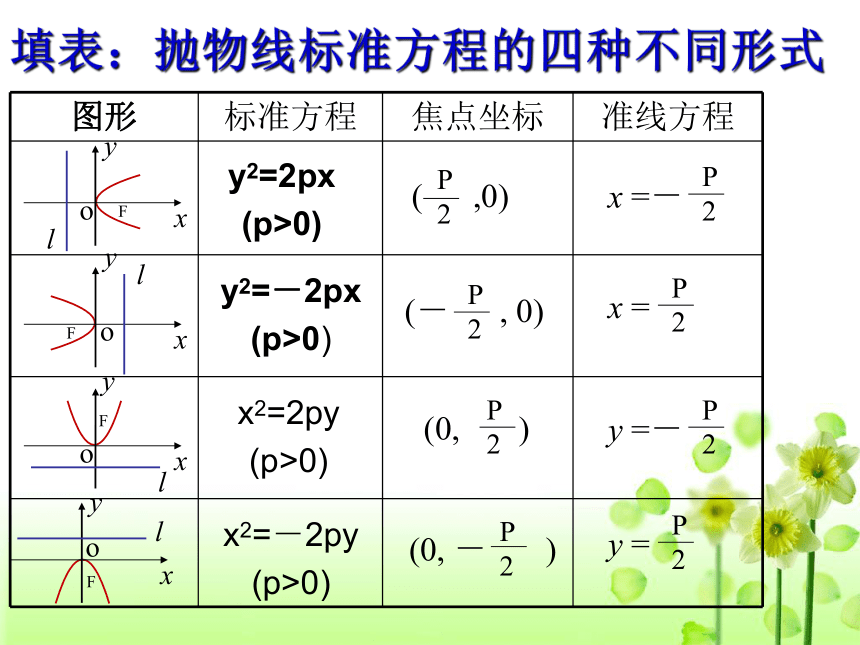
yxo3.抛物线的标准方程:填表:抛物线标准方程的四种不同形式y2=-2px
(p>0)x2=-2py
(p>0)x2=2py
(p>0)例1、(1)已知抛物线的标准方程是 y2 = 6x,求它的
焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程;(3)已知抛物线的标准方程是 y= 6x2,求它的焦点坐标和
准线方程;例题与练习:练习1:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(3)焦点到准线的距离是2 .例题2 已知抛物线经过点(-4,-2),求它的标准方程.练习2:求过点A(-3,2)的抛物线的标准方程 .求焦点在直线 x-2y-4=0 上的抛物线的标准方程.练习3:2.4.2抛物线的简单几何性质的应用一、复习(一) 抛物线的定义 平面内与一个 定 点F和一条 定 直线l(l不经过点F)的距离 相等 的点的轨迹叫做抛物线.
其中:F叫做抛物线的 焦 点,l叫做抛物线的 准 线.(二) 抛物线的标准方程一、复习(一) 抛物线的定义 平面内与一个 定 点F和一条 定 直线l(l不经过点F)的距离 相等 的点的轨迹叫做抛物线.
其中:F叫做抛物线的 焦 点,l叫做抛物线的 准 线.(二) 抛物线的标准方程(1)开口向右y2 = 2px (p>0)(2)开口向左y2 = -2px (p>0)(3)开口向上x2 = 2py (p>0)(4)开口向下x2 = -2py (p>0)其中p的几何意义为焦点到准线的距离.抛物线的几何性质抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。1、范围由抛物线y2 =2px(p>0)2、对称性定义:抛物线和它的轴的交点称为抛物线
的顶点。由y2 = 2px (p>0)当y=0时,x=0, 因此抛物线的顶点就是坐标原点(0,0)。注:这与椭圆有四个顶点,双曲线有两个顶点不同。3、顶点4、离心率 抛物线上的点与焦点的距离和它到准线的距离 之比,叫做抛物线的离心率,由抛物线的定义,可知e=1。所以可设它的标准方程为y2=2px(p>0)所求方程为y2=8x。即 p = 4∵点M在抛物线上,∴抛物线的准线方程为x=-2.分析:可设它的标准方程为y2=2px(p>0)
或x2=2py(p>0)(解法二:利用抛物线定义可将|AB|的长度
转化为A、B两点到准线的距离和,然后用
韦达定理求解。)提示(解法一:联立方程组求解A、B两点坐标,
利用两点距离公式即可。)引申 AB的长度为 总结掌握抛物线的几何性质;在分析和解决问题时,注意画草图来帮助我们分析.过焦点的弦称为焦点弦;解决焦点弦问题要注意数形结合,等价转化等思想方法.1、2、 目标检测
定点F:抛物线的焦点
定直线l:抛物线的准线
解:取过点F且垂直于直线l的直线为x轴,垂足为K,以KF的中垂线为y轴,建立直角坐标系,如图。设
yxo3.抛物线的标准方程:填表:抛物线标准方程的四种不同形式y2=-2px
(p>0)x2=-2py
(p>0)x2=2py
(p>0)例1、(1)已知抛物线的标准方程是 y2 = 6x,求它的
焦点坐标和准线方程;(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程;(3)已知抛物线的标准方程是 y= 6x2,求它的焦点坐标和
准线方程;例题与练习:练习1:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(3)焦点到准线的距离是2 .例题2 已知抛物线经过点(-4,-2),求它的标准方程.练习2:求过点A(-3,2)的抛物线的标准方程 .求焦点在直线 x-2y-4=0 上的抛物线的标准方程.练习3:2.4.2抛物线的简单几何性质的应用一、复习(一) 抛物线的定义 平面内与一个 定 点F和一条 定 直线l(l不经过点F)的距离 相等 的点的轨迹叫做抛物线.
其中:F叫做抛物线的 焦 点,l叫做抛物线的 准 线.(二) 抛物线的标准方程一、复习(一) 抛物线的定义 平面内与一个 定 点F和一条 定 直线l(l不经过点F)的距离 相等 的点的轨迹叫做抛物线.
其中:F叫做抛物线的 焦 点,l叫做抛物线的 准 线.(二) 抛物线的标准方程(1)开口向右y2 = 2px (p>0)(2)开口向左y2 = -2px (p>0)(3)开口向上x2 = 2py (p>0)(4)开口向下x2 = -2py (p>0)其中p的几何意义为焦点到准线的距离.抛物线的几何性质抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。1、范围由抛物线y2 =2px(p>0)2、对称性定义:抛物线和它的轴的交点称为抛物线
的顶点。由y2 = 2px (p>0)当y=0时,x=0, 因此抛物线的顶点就是坐标原点(0,0)。注:这与椭圆有四个顶点,双曲线有两个顶点不同。3、顶点4、离心率 抛物线上的点与焦点的距离和它到准线的距离 之比,叫做抛物线的离心率,由抛物线的定义,可知e=1。所以可设它的标准方程为y2=2px(p>0)所求方程为y2=8x。即 p = 4∵点M在抛物线上,∴抛物线的准线方程为x=-2.分析:可设它的标准方程为y2=2px(p>0)
或x2=2py(p>0)(解法二:利用抛物线定义可将|AB|的长度
转化为A、B两点到准线的距离和,然后用
韦达定理求解。)提示(解法一:联立方程组求解A、B两点坐标,
利用两点距离公式即可。)引申 AB的长度为 总结掌握抛物线的几何性质;在分析和解决问题时,注意画草图来帮助我们分析.过焦点的弦称为焦点弦;解决焦点弦问题要注意数形结合,等价转化等思想方法.1、2、 目标检测
