上海市浦东新区第四教育署2017-2018学年度九年级(五四学制)上学期期中质量调研数学试卷(含答案)
文档属性
| 名称 | 上海市浦东新区第四教育署2017-2018学年度九年级(五四学制)上学期期中质量调研数学试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-08 00:00:00 | ||
图片预览




文档简介
2017学年第一学期期中质量调研
初三数学试卷
(考试时间100分钟,满分150分)
题号
一
二
三
四
总分
得分
一、选择题:(本大题共6题,每题4分,满分24分)
1.已知两个相似三角形的周长比为4:9,则它们的面积比为(
)
A.4:9
B.2:3
C.8:18
D.16:49
2.如图,在△ABC中,∠ADE
=
∠B,DE
:BC
=
2
:3,
则下列结论正确的是(
)
A.
AD
:
AB
=
2
:
3;
B.AE
:
AC
=
2:5;
C.
AD
:
DB
=
2
:
3;
D.CE
:
AE=
3
:
2.
3.在正方形网格中,△ABC的位置如图所示,则cos∠B的值为(
)
A.;
B.;
C.;
D..
4.
如图,已知向量,,,那么下列结论正确的是(
)
A.
B.
C.
D.
5.已知P为线段AB的黄金分割点,且AP<PB,则(
)
A.
AP2=AB·PB
;
B.
AB2=AP·PB
;
C.
PB2=AP·AB
;
D.
AP2+BP2=AB2.
6.
P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?(
)
A.
1条
B.
2条
C.
3条
D.4条
二、填空题:(本大题共12题,每题4分,满分48分)
7.
已知,那么=
.
8.
已知线段a=2cm、b=8cm,那么线段a、b的比例中项等于
cm..
9.
计算:=____________.
10.点是的重心,如果,,那么的长是
.
11.在△ABC中,已知点D、E分别在边AB、AC上,DE∥BC.如果AD=1cm,AB=3cm,DE=4cm,那么BC=
cm.
12.
如图,平行四边形中,是边上的点,交于点,如果,那么
.
13.如图,直线////,,,那么的值是
.
14.在中,,BC=6,,那么
.
15.如图,在△ABC中,点D在AB上,请再添一个适当的条件,
使△ADC∽△ACB,那么可添加的条件是
.
16.如图,已知点D、E分别在△ABC边AB、AC上,DE//BC,,那么=
.
17.在中,,点D在AC上,BD平分,将△BCD沿着直线BD翻折,点C落在处,如果,,那么的值是
.
18.
新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在中,,,,如果准外心在边上,那么的长为
.
19.(本题满分10分)
计算:
20.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)
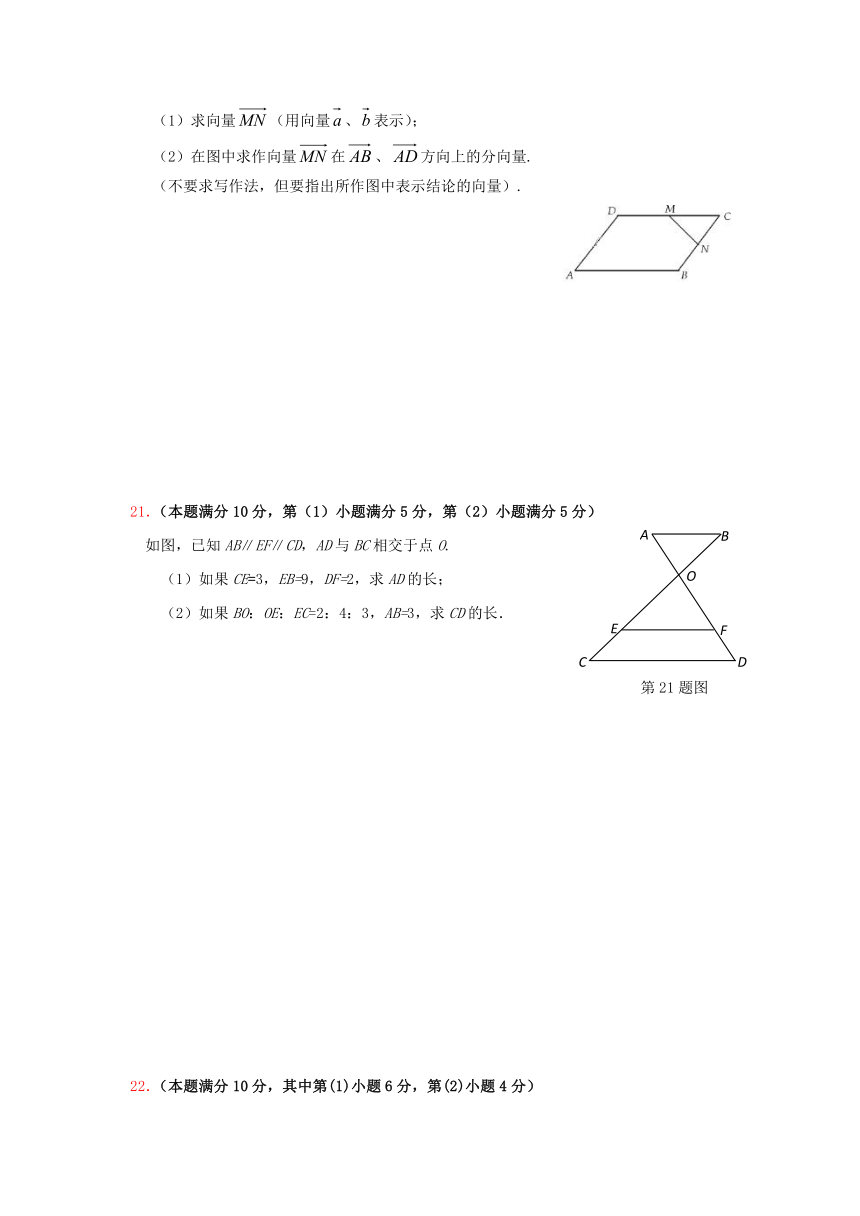
如图,已知平行四边形ABCD,点M、N是边DC、BC的中点,设,.
(1)求向量(用向量、表示);
(2)在图中求作向量在、方向上的分向量.
(不要求写作法,但要指出所作图中表示结论的向量).
21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)
如图,已知AB∥EF∥CD,AD与BC相交于点O.
(1)如果CE=3,EB=9,DF=2,求AD的长;
(2)如果BO:OE:EC=2:4:3,AB=3,求CD的长.
22.(本题满分10分,其中第(1)小题6分,第(2)小题4分)
如图,在中,,点D是BC边上的一点,,,
.
(1)求AC和AB的长;
(2)求的值.
四、解答题:(本大题共3题,满分38分)
23.(本题满分12分,每小题满分6分)
已知:如图10,在△ABC中,点D、E分别在边AB、AC上,且∠ABE
=∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
24.(本题满分12分,每小题满分4分)
如图所示,在△ABC中,已知,边上中线。点P为线段AD上一点(与点A、D不重合),过P点作EF∥BC,分别交边AB、AC于点E、F,过点E、F分别作EG∥AD,FH∥AD,交BC边于点G、H.
(1)求证:P是线段EF的中点;
(2)当四边形EGHF为菱形时,求EF的长;
(3)
如果,设AP长为,四边形EGHF面积为,求关于的函数解析式及其定义域.
25.(本题满分14分,第(1)题满分4分,第(2)小题满分6分,第(3)小题满分4分)
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
(1)若△CEF与△ABC相似,且当AC=BC=2时,求AD的长;
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,求AD的长;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
2017学年第一学期期中初三年级数学调研试卷
命题说明
考试范围:第二十四章、第二十五章(至25.3解直角三角形为止)
试卷安排:
总分150分;
考试时间:100分钟
试卷一共三道大题:
(一)、选择题
6道(每道4分,共计24分)
(二)、填空题12道(每道4分,共计48分)
(三)、简答题
4题(每道10分,满分40分)
(四)、解答题
3题(满分38分)
三、
期望值:115分
2017学年第一学期期中初三年级数学调研试卷
参考答案
一、选择题:(本大题共6题,每题4分,满分24分)
1.
D
2.
A
3.
B
4.
D
5.
C
6.
C
二、填空题:(本大题共12题,每题4分,满分48分)
7.
;
8.
4;
9.;
10.
8;
11.
12;
12.;
13.
4;
14.
;
15.
等;
16.
;
17.
;
18.
4或.
三、简答题:(本大题共4题,满分40分)
19.(本题10分)解:原式=
5分
=
3分
=
2分
20.(本题10分)解:(1)
2分
2分
2分
(2)略作图
2分,
结论
2分
21.(本题10分)(1)解:
2分
1分
1分
1分
(2)解:
2分
1分
又
1分
1分
22.解:(1)在Rt△ACD中,cos∠ADC=
……………………………1分
∵cos∠ADC=,CD=6
,
∴AD=10
………………………………
1分
∴AC=…………………………………………………
1分
在Rt△ACB中,tanB=
……………………………1分
∵tanB=,AC=8
,
∴CB=12
………………………………
1分
∴AB=……………………………………………
1分
作DH⊥AB,交AB于点H,
则∠BHD=∠C=90
在△BHD与△BCA中
∴△BHD∽△BCA
…………………………………………
1分
∴
即
…………………………………………
1分
∴DH=
…………………
1分
∴在Rt△ADH中,sin∠BAD=
……
1分
23.(本题满分12分,其中每小题各6分)
解:(1)∵∠ABE
=∠ACD,且∠A是公共角,
∴△ABE∽△ACD.……………………………………………………………………2分
∴,即.
………………………………………………………1分
又∵∠A是公共角,
…………………………………………………………………1分
∴△AED∽△ABC.
……………………………………………………………………2分
(2)∵∠ABE
=∠ACD,∠BGD
=∠CGE,
∴
△BGD∽△CGE.
……………………………………………………………………1分
∴,即.
又∵∠DGE
=∠BGC,
∴△DGE∽△BGC.………………………………………………………………………2分
∴∠GBC
=∠GDE,………………………………………………………………………1分
∵BE平分∠ABC,∴∠GBC
=∠ABE,
∵∠ABE
=∠ACD,
∴∠GDE
=∠ACD.………………………………………………………………………1分
∴DE=CE.
………………………………………………………………………………1分
24.解:∵EF∥BC,∴;.
……………………2分
∴.
……………………………………………………………1分
又∵BD=CD,∴EP=FP,即P是EF中点.
…………………………1分
(2)∵EF∥BC,∴△AEF∽△ABC.
…………………………………1分
∴,
……………………………………………………………1分
设,则.∴,解得.
……………
2分
(3)∵EF∥BC,EG∥FH,∴四边形EGHF是平行四边形.
作PQ⊥BC,垂足为Q,则.
………
1分
由(2)得,,.
…………………………
1分
∴
.
………………………………
2分
25.解:(1)若△CEF与△ABC相似,且当AC=BC=2时,
△ABC为等腰直角三角形,如答图1所示.
……………………………………………………
图
1分
此时D为AB边中点
……………………………………………………………
1分
AD=AC=.
……………………………………………………………
2分
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,有两种情况:
(I)若CE:CF=3:4,如答图2所示.
∵CE:CF=AC:BC,∴EF∥BC.
由折叠性质可知,CD⊥EF,∴CD⊥AB,即此时CD为AB边上的高.………………
1分
在Rt△ABC中,AC=3,BC=4,∴BC=5,∴cosA=.
AD=AC cosA=3×=1.8;
……………………………………………………………
2分
(II)若CF:CE=3:4,如答图3所示.
∵△CEF∽△CAB,∴∠CEF=∠B.
………………………………………………………1分
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴此时AD=AB=×5=2.5.
……………………………………………………………
2分
综上所述,当AC=3,BC=4时,AD的长为1.8或2.5.
(3)当点D是AB的中点时,△CEF与△ABC相似.理由如下:
如答图3所示,连接CD,与EF交于点Q.
∵CD是Rt△ABC的中线,∴CD=DB=AB,∴∠DCB=∠B.
1分
由折叠性质可知,∠CQF=∠DQF=90°,∴∠DCB+∠CFE=90°,
∵∠B+∠A=90°,∴∠CFE=∠A,
2分
又∵∠C=∠C,∴△CEF∽△CBA
1分
第3题图
E
C
D
A
F
B
第16题图
A
D
C
B
E
A
B
C
D
E
第21题图
F
O
D
A
B
C
图10
初三数学试卷
(考试时间100分钟,满分150分)
题号
一
二
三
四
总分
得分
一、选择题:(本大题共6题,每题4分,满分24分)
1.已知两个相似三角形的周长比为4:9,则它们的面积比为(
)
A.4:9
B.2:3
C.8:18
D.16:49
2.如图,在△ABC中,∠ADE
=
∠B,DE
:BC
=
2
:3,
则下列结论正确的是(
)
A.
AD
:
AB
=
2
:
3;
B.AE
:
AC
=
2:5;
C.
AD
:
DB
=
2
:
3;
D.CE
:
AE=
3
:
2.
3.在正方形网格中,△ABC的位置如图所示,则cos∠B的值为(
)
A.;
B.;
C.;
D..
4.
如图,已知向量,,,那么下列结论正确的是(
)
A.
B.
C.
D.
5.已知P为线段AB的黄金分割点,且AP<PB,则(
)
A.
AP2=AB·PB
;
B.
AB2=AP·PB
;
C.
PB2=AP·AB
;
D.
AP2+BP2=AB2.
6.
P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?(
)
A.
1条
B.
2条
C.
3条
D.4条
二、填空题:(本大题共12题,每题4分,满分48分)
7.
已知,那么=
.
8.
已知线段a=2cm、b=8cm,那么线段a、b的比例中项等于
cm..
9.
计算:=____________.
10.点是的重心,如果,,那么的长是
.
11.在△ABC中,已知点D、E分别在边AB、AC上,DE∥BC.如果AD=1cm,AB=3cm,DE=4cm,那么BC=
cm.
12.
如图,平行四边形中,是边上的点,交于点,如果,那么
.
13.如图,直线////,,,那么的值是
.
14.在中,,BC=6,,那么
.
15.如图,在△ABC中,点D在AB上,请再添一个适当的条件,
使△ADC∽△ACB,那么可添加的条件是
.
16.如图,已知点D、E分别在△ABC边AB、AC上,DE//BC,,那么=
.
17.在中,,点D在AC上,BD平分,将△BCD沿着直线BD翻折,点C落在处,如果,,那么的值是
.
18.
新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在中,,,,如果准外心在边上,那么的长为
.
19.(本题满分10分)
计算:
20.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)
如图,已知平行四边形ABCD,点M、N是边DC、BC的中点,设,.
(1)求向量(用向量、表示);
(2)在图中求作向量在、方向上的分向量.
(不要求写作法,但要指出所作图中表示结论的向量).
21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)
如图,已知AB∥EF∥CD,AD与BC相交于点O.
(1)如果CE=3,EB=9,DF=2,求AD的长;
(2)如果BO:OE:EC=2:4:3,AB=3,求CD的长.
22.(本题满分10分,其中第(1)小题6分,第(2)小题4分)
如图,在中,,点D是BC边上的一点,,,
.
(1)求AC和AB的长;
(2)求的值.
四、解答题:(本大题共3题,满分38分)
23.(本题满分12分,每小题满分6分)
已知:如图10,在△ABC中,点D、E分别在边AB、AC上,且∠ABE
=∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
24.(本题满分12分,每小题满分4分)
如图所示,在△ABC中,已知,边上中线。点P为线段AD上一点(与点A、D不重合),过P点作EF∥BC,分别交边AB、AC于点E、F,过点E、F分别作EG∥AD,FH∥AD,交BC边于点G、H.
(1)求证:P是线段EF的中点;
(2)当四边形EGHF为菱形时,求EF的长;
(3)
如果,设AP长为,四边形EGHF面积为,求关于的函数解析式及其定义域.
25.(本题满分14分,第(1)题满分4分,第(2)小题满分6分,第(3)小题满分4分)
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
(1)若△CEF与△ABC相似,且当AC=BC=2时,求AD的长;
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,求AD的长;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
2017学年第一学期期中初三年级数学调研试卷
命题说明
考试范围:第二十四章、第二十五章(至25.3解直角三角形为止)
试卷安排:
总分150分;
考试时间:100分钟
试卷一共三道大题:
(一)、选择题
6道(每道4分,共计24分)
(二)、填空题12道(每道4分,共计48分)
(三)、简答题
4题(每道10分,满分40分)
(四)、解答题
3题(满分38分)
三、
期望值:115分
2017学年第一学期期中初三年级数学调研试卷
参考答案
一、选择题:(本大题共6题,每题4分,满分24分)
1.
D
2.
A
3.
B
4.
D
5.
C
6.
C
二、填空题:(本大题共12题,每题4分,满分48分)
7.
;
8.
4;
9.;
10.
8;
11.
12;
12.;
13.
4;
14.
;
15.
等;
16.
;
17.
;
18.
4或.
三、简答题:(本大题共4题,满分40分)
19.(本题10分)解:原式=
5分
=
3分
=
2分
20.(本题10分)解:(1)
2分
2分
2分
(2)略作图
2分,
结论
2分
21.(本题10分)(1)解:
2分
1分
1分
1分
(2)解:
2分
1分
又
1分
1分
22.解:(1)在Rt△ACD中,cos∠ADC=
……………………………1分
∵cos∠ADC=,CD=6
,
∴AD=10
………………………………
1分
∴AC=…………………………………………………
1分
在Rt△ACB中,tanB=
……………………………1分
∵tanB=,AC=8
,
∴CB=12
………………………………
1分
∴AB=……………………………………………
1分
作DH⊥AB,交AB于点H,
则∠BHD=∠C=90
在△BHD与△BCA中
∴△BHD∽△BCA
…………………………………………
1分
∴
即
…………………………………………
1分
∴DH=
…………………
1分
∴在Rt△ADH中,sin∠BAD=
……
1分
23.(本题满分12分,其中每小题各6分)
解:(1)∵∠ABE
=∠ACD,且∠A是公共角,
∴△ABE∽△ACD.……………………………………………………………………2分
∴,即.
………………………………………………………1分
又∵∠A是公共角,
…………………………………………………………………1分
∴△AED∽△ABC.
……………………………………………………………………2分
(2)∵∠ABE
=∠ACD,∠BGD
=∠CGE,
∴
△BGD∽△CGE.
……………………………………………………………………1分
∴,即.
又∵∠DGE
=∠BGC,
∴△DGE∽△BGC.………………………………………………………………………2分
∴∠GBC
=∠GDE,………………………………………………………………………1分
∵BE平分∠ABC,∴∠GBC
=∠ABE,
∵∠ABE
=∠ACD,
∴∠GDE
=∠ACD.………………………………………………………………………1分
∴DE=CE.
………………………………………………………………………………1分
24.解:∵EF∥BC,∴;.
……………………2分
∴.
……………………………………………………………1分
又∵BD=CD,∴EP=FP,即P是EF中点.
…………………………1分
(2)∵EF∥BC,∴△AEF∽△ABC.
…………………………………1分
∴,
……………………………………………………………1分
设,则.∴,解得.
……………
2分
(3)∵EF∥BC,EG∥FH,∴四边形EGHF是平行四边形.
作PQ⊥BC,垂足为Q,则.
………
1分
由(2)得,,.
…………………………
1分
∴
.
………………………………
2分
25.解:(1)若△CEF与△ABC相似,且当AC=BC=2时,
△ABC为等腰直角三角形,如答图1所示.
……………………………………………………
图
1分
此时D为AB边中点
……………………………………………………………
1分
AD=AC=.
……………………………………………………………
2分
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,有两种情况:
(I)若CE:CF=3:4,如答图2所示.
∵CE:CF=AC:BC,∴EF∥BC.
由折叠性质可知,CD⊥EF,∴CD⊥AB,即此时CD为AB边上的高.………………
1分
在Rt△ABC中,AC=3,BC=4,∴BC=5,∴cosA=.
AD=AC cosA=3×=1.8;
……………………………………………………………
2分
(II)若CF:CE=3:4,如答图3所示.
∵△CEF∽△CAB,∴∠CEF=∠B.
………………………………………………………1分
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠A=∠ECD,∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴此时AD=AB=×5=2.5.
……………………………………………………………
2分
综上所述,当AC=3,BC=4时,AD的长为1.8或2.5.
(3)当点D是AB的中点时,△CEF与△ABC相似.理由如下:
如答图3所示,连接CD,与EF交于点Q.
∵CD是Rt△ABC的中线,∴CD=DB=AB,∴∠DCB=∠B.
1分
由折叠性质可知,∠CQF=∠DQF=90°,∴∠DCB+∠CFE=90°,
∵∠B+∠A=90°,∴∠CFE=∠A,
2分
又∵∠C=∠C,∴△CEF∽△CBA
1分
第3题图
E
C
D
A
F
B
第16题图
A
D
C
B
E
A
B
C
D
E
第21题图
F
O
D
A
B
C
图10
同课章节目录
