运用基本不等式求最值专题讲座

课件33张PPT。 深圳市民办学校
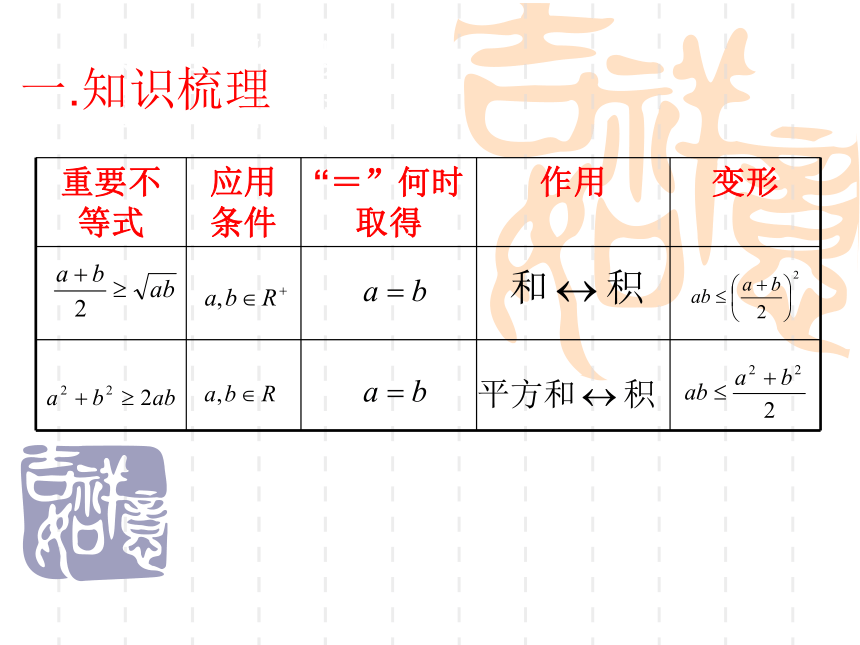
高中数学教师欧阳文丰基本不等式求最值一、知识梳理
1.重要的不等式
一.知识梳理2、已知 都是正数，
（1）如果积 是定值P，那么当 时，
和 有最小值
（2）如果和 是定值S，那么当 时，积 有最大值讲授新课：一、配凑法求最值当且仅当a=b=2时等号成立所以ab的最大值为4解：当且仅当2a=b时等号成立，即a=1,b=2时ab的最大值为2当且仅当a= 时等号成立，即a=2,b=4时，
ab的最大值为8.解:已知a>0,b>0,且的最大值。变式3：题型二：拆项法求函数的最值类型三 ：含两个变量的最值问题
例5 （1)已知 且 ，求 的最小值.
（2）已知正数 满足 ，求 的
最小值.
类型三 ：含两个变量的最值问题例5、当0解析 x∈(0, ),1-2x＞0,又2x+(1-2x)=1，
原式可化为:25类型三 ：含两个变量的最值问题变式训练利用基本不等式，整体解决消元类型四：分子化为常数型，分母应用基本不等式
1. 两个不等式
（1）
（2） 当且仅当a=b时，等号成立
注意：1.两公式条件，前者要求a,b为实数；后者要求a,b为正数。
2.公式的正向、逆向使用的条件以及“=”的成立条件。
2.不等式的简单应用：主要在于求最值
把握 “七字方针” 即 “一正，二定，三相等”课堂小结3. 利用基本不等式求最值时，如果无定值，要先配、凑出定值，再利用基本不等式求解。1、 (1)a,b都是正数且2a＋b＝2,求a(1＋b)
的最值和此时a、b的值.(2)作业：作业：（4）作业：3、（1）若x>3,求函数 的最小值4、作业：