24.1.1圆的概念 课件

课件27张PPT。 耶稣带着他的门徒彼得远行，途中发现一块破烂的马蹄铁，耶稣就让彼得把它捡起来。不料彼得懒得弯腰假装没听见，耶稣没说什么就自己弯腰捡起马蹄铁，用它从铁匠那儿换来3文钱，用这钱买了18颗樱桃。出了城，两人继续前进，经过的全是茫茫的荒野。耶稣猜到彼得渴得够呛，就让藏于袖中的樱桃悄悄地掉出一颗，彼得一见，赶紧捡起来吃。耶稣边走边丢，彼得也就狼狈地弯了18次腰。于是耶稣笑着对他说：“要是你刚才弯一次腰，就不会在后来没完没了地弯腰。小事不干，将来就会在更小的事情上操劳。”
今天不弯腰，明天就会折腰启示：成功要付出一定的代价，但不成功是一定要付出代价的，而且不成功所付出的代价更大更惨重！长痛不如短痛。方法可以简化，但努力不可以简化！看起来很复杂的事情，你一做起来，一行动起来，持续行动起来，就会越来越简单了。越不去做就越复杂！圆是生活中常见的图形，许多物体都给我们以圆的形象.一 感知圆的世界24.1.1 圆诗人笔下的圆大漠孤烟直，
长河落日圆．
海上生明月，
天涯共此时．
水 滴 画 圆
激 扬 生 命树 木 画 圆
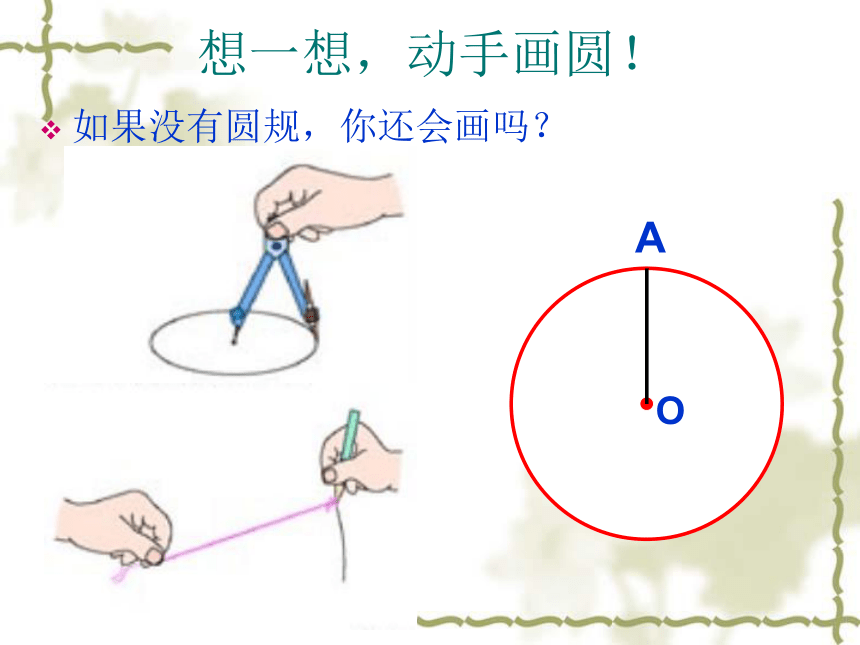
彰 显 苍 劲大自然会画圆，你会画圆吗？想一想，动手画圆！如果没有圆规，你还会画吗？OA 如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆．其中固定的端点O叫做圆心，线段
OA叫做半径。以点O为圆心的圆，记作“⊙O”，读作“圆O”．二、圆的概念思考：
1、根据以上定义，“圆”指的是“圆周”还是“圆面”？圆指的是圆周OA思考：
1、以定点O为圆心能画几个圆？
2、以定长r为半径能画几个圆？
3、以定点O为圆心，定长r为半径能画几个圆？
4、确定一个圆的要素有哪些？Or无数个无数个只有一个确定圆的要素是圆心和半径，圆心确定圆的位置，半径确定圆的大小确定圆的要素 如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆．二、圆的概念思考：
1、圆上的每一个点到定点O的距离都相等吗？
2、在这个平面上到定点O的距离都等于定长OA的点都在这个圆上吗？有例外的吗？都相等都在，没有例外的点。（1）圆上各点到定点（圆心O）的距离都等于定长（半径r）；（2）到定点的距离等于定长的点都在同一个圆上． 圆也可以看成（在同一平面内）是所有到定点的距离等于定长的点的集合。我国古人很早对圆就有这样的认识了，战国时的《墨经》就有“圆，一中同长也”的记载．它的意思是圆上各点到圆心的距离都等于半径．这一发现比西方早了一千多年！·rOA（1）圆上各点到定点（圆心O）的距离都等于定长（半径r）；（2）到定点的距离等于定长的点都在同一个圆上．问题：1、若点A、点B、点C等都在 上，则OA、OB、OC有什么关系？
2、若OA=OB=OC，则A、B、C三点在同一个圆上吗？⊙OBCOA=OB=OC（同圆的半径处处相等）A、B、C三点在以点O为圆心OA为半径的圆上议一议、说一说1、车轮为什么做成圆形的？试想一下，如果车轮不是圆的（比如三角形或正方形的），坐车的人会是什么感觉？议一议、说一说2、如果车轮做成三角形或正方形的，坐车的人会是什么感觉？ 把车轮做成圆形，车轮上各点到车轮中心（圆心）的距离都等于车轮的半径，当车轮在平面上滚动时，车轮中心与平面的距离保持不变，因此，当车辆在平坦的路上行驶时，坐车的人会感到非常平稳，这就是车轮都做成圆形的数学道路。圆上的点到圆心的距离是一个定值车轮为什么做成圆形的？归纳总结 例1：矩形ABCD的对角线AC、BD相交于点O。
求证：A，B，C，D四个点在以点O为圆心的同一个圆上。例题证明：∵ABCD是矩形 ∴AO=OC= AC;OB=OD= BD；AC=BD
∴OA=OB=OC=OD∴A、B、C、D在以O为圆心以OA为半径的圆上。
矩形－－四点共圆。 3.连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心的弦叫做直径(如直径AC).AB注意：
（1）弦的两个端点在圆上.
（2）直径是弦，是过圆心的弦，
　弦不一定是直径.
（3)半径不是弦，因为圆心不在圆周上.弦.OADQCBPHGFE１.如图(1)直径是_______;

(2)弦是_____________;

(3) PQ是直径吗?______;

(4)线段EF、GH
是弦吗？_______.KABCD、DK、AB不是不是及时反馈一议一议小明和小强为了探究 , O中有没有最长的弦?
经过了大量的测量，最后得出一致结论，直径
是圆中最长的弦，你认为他们的结论对吗？
试说说你的理由.⊙直径是圆中最长的弦圆上任意两点间的部分叫做 圆弧，简称弧．以A、B为端点的弧记作 ，读作“圆弧AB”或“弧AB”．圆的任意一条直径 的两个端点把圆分成两条弧，每一条弧都叫做 半 圆．·OAB弧·BOA·COAB劣弧与优弧 小于半圆的弧（如图中的　　）叫做劣弧；（常用两个字母表示）大于半圆的弧（常用三个字母表示，
如图中的 ）叫做优弧.ABC⌒弧有三类，分别是优弧、劣弧、半圆。●OBCA 1.如图,
2 .劣弧有：优弧有：它们一样么？等圆能够重合的两个圆是等圆。容易看出：半径相等的两个圆是等圆；反过来，同圆或等圆的半径相等。·BO1A等弧在同圆或等圆中，能够互相重合的弧叫做等弧。·DO2FEC长度相等的两段弧是等弧吗？为什么？（ ）想一想判断下列说法的正误：(1)弦是直径；( )(2)半圆是弧； ( )(3)过圆心的线段是直径； ( ) (7)半径相等的两个圆是等圆.( )(4)过圆心的直线是直径；( )(5)半圆是最长的弧；( )(6)直径是最长的弦；( ) 巩固练习1.如何在操场上画一个半径 是5m的圆？说出你的理由首先确定圆心, 然后用5米长的绳子一端固定为圆心端,另一端系在一端尖木棒,木棒以5米长尖端划动一周,所形成的图形就是所画的圆.根据圆的形成定义练一练2 你见过树木的年轮吗?从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径 是23cm,这棵红杉树的半径 每年增加多少?.解:
23÷2÷20=0.575cm 答: 这棵红衫树的半径 每年增加0.575cm 练一练3、△ABC中，∠C=90°。
求证：A，B，C三点在同一个圆上。ACB证明：取AB的中点O，连接OC∵∠ACB=90°，AO=BO
∴OA=OC=OB
∴A，B，C三点在以点O为圆心，OA为半径的圆上。1.本节课我学到了 ；

2.本节课我还不太理解的地方有 。
归纳小结 结束寄语
圆规为什么可以画圆？因为心已定，脚在动。你为什么不能圆梦？因为心不定，脚不动。作业课本89页第一、二题