《4.1.1 立体图形与平面图形》同步练习(含答案)
文档属性
| 名称 | 《4.1.1 立体图形与平面图形》同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 356.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-13 10:09:47 | ||
图片预览

文档简介
《立体图形与平面图形》同步练习
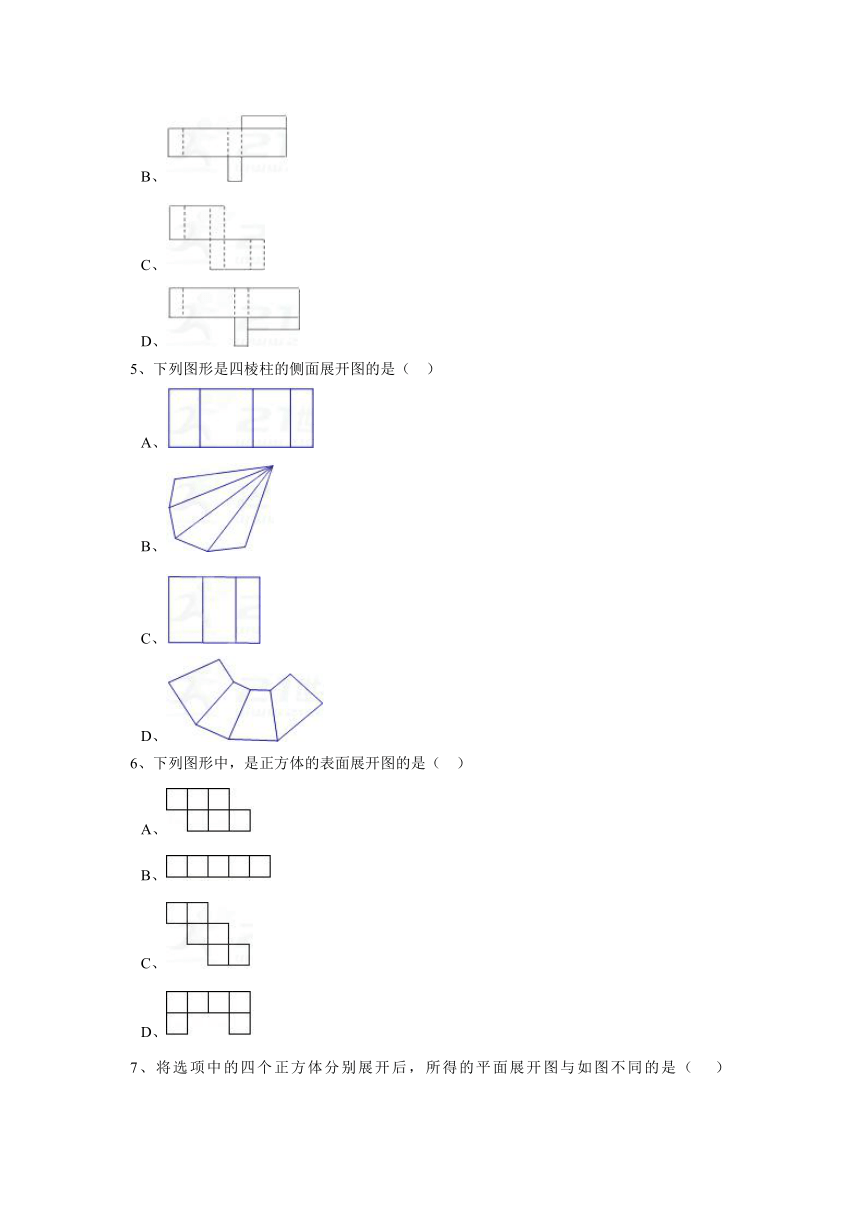
1、下列说法中,正确的是(
)
A、用一个平面去截一个圆锥,可以是椭圆
B、棱柱的所有侧棱长都相等
C、用一个平面去截一个圆柱体,截面可以是梯形
D、用一个平面去截一个长方体截面不能是正方形
2、下列说法不正确的是(
)
A、球的截面一定是圆
B、组成长方体的各个面中不可能有正方形
C、从三个不同的方向看正方体,得到的都是正方形
D、圆锥的截面可能是圆
3、下列图形中,是棱锥展开图的是(
)
A、
B、
C、
D、
4、下面图形不能围成一个长方体的是(
)
A、
B、
C、
D、
5、下列图形是四棱柱的侧面展开图的是(
)
A、
B、
C、
D、
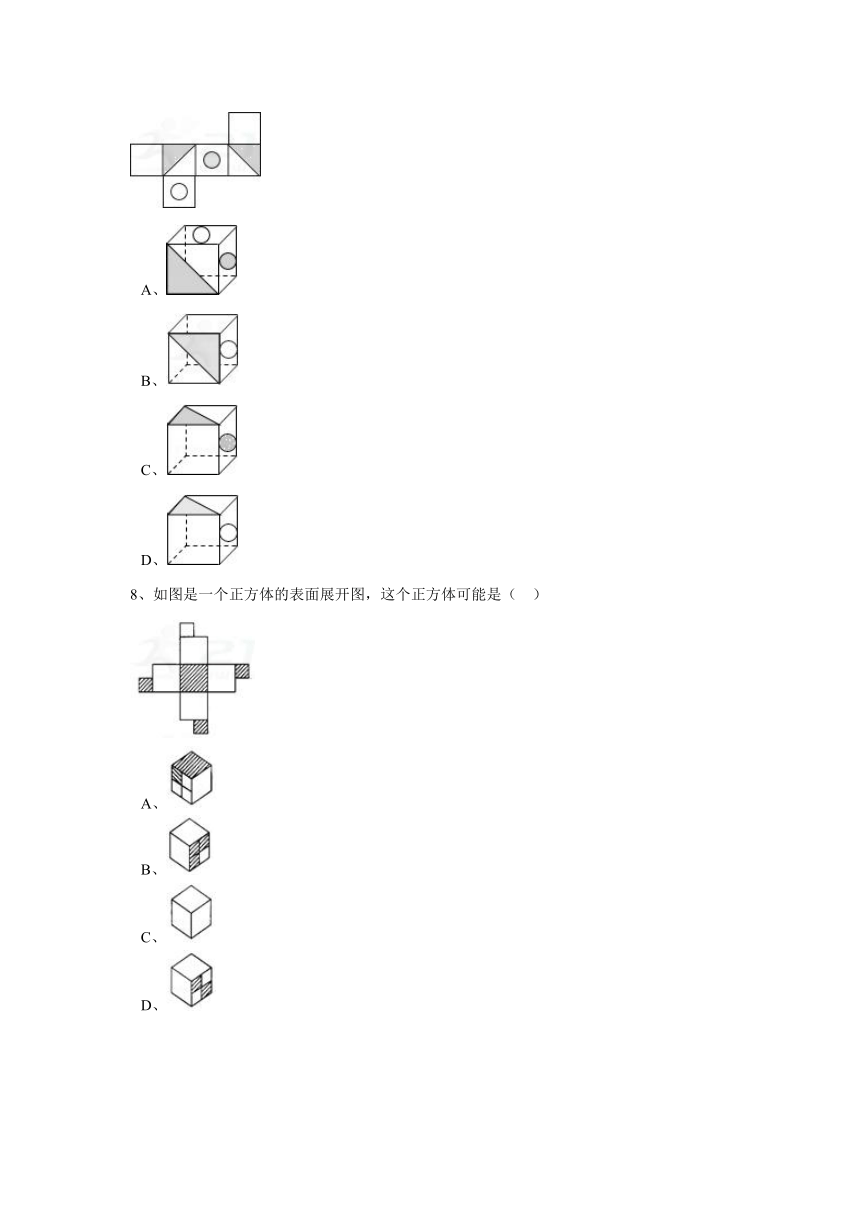
6、下列图形中,是正方体的表面展开图的是(
)
A、
B、
C、
D、
7、将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的是(
)
A、
B、
C、
D、
8、如图是一个正方体的表面展开图,这个正方体可能是(
)
A、
B、
C、
D、
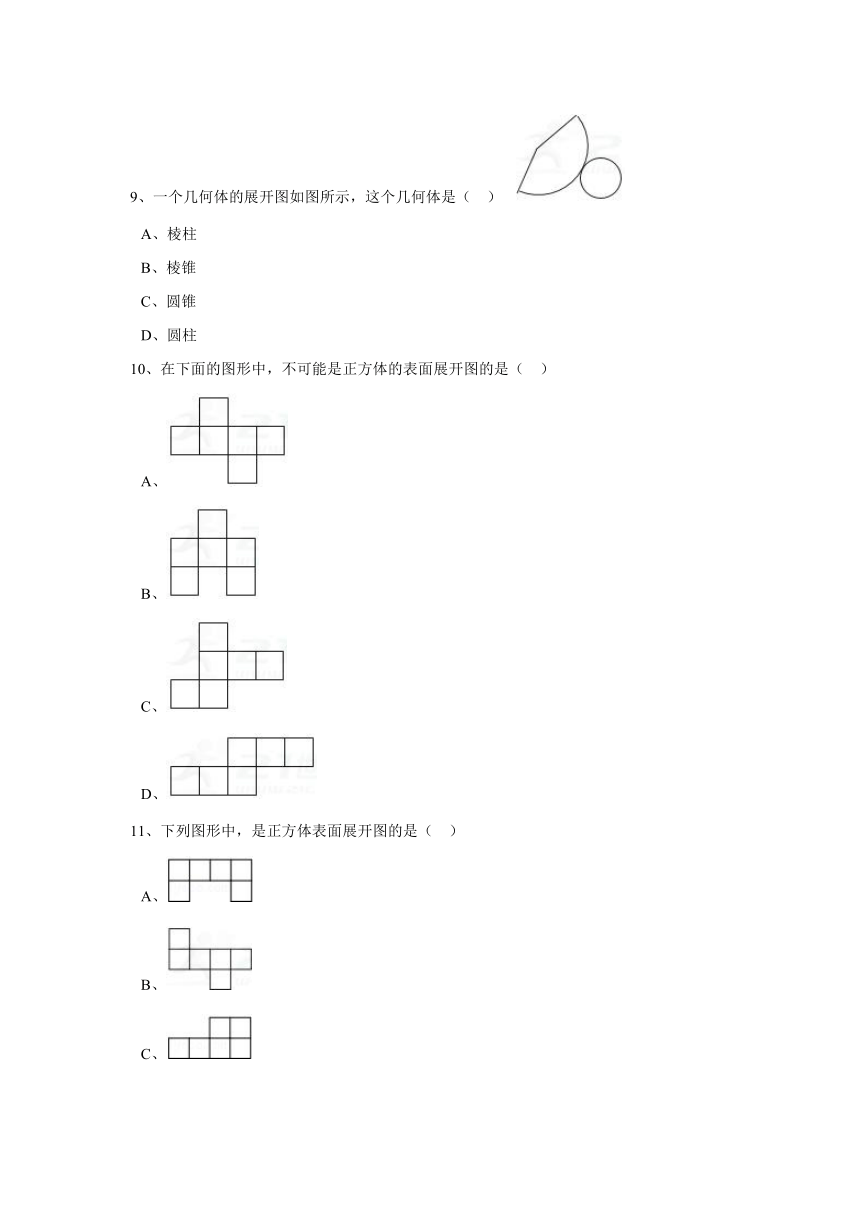
9、一个几何体的展开图如图所示,这个几何体是(
)
A、棱柱
B、棱锥
C、圆锥
D、圆柱
10、在下面的图形中,不可能是正方体的表面展开图的是(
)
A、
B、
C、
D、
11、下列图形中,是正方体表面展开图的是(
)
A、
B、
C、
D、
12、下列四个图形中是如图展形图的立体图的是(
)
A、
B、
C、
D、
13、一个棱锥有7个面,这是________棱锥。
14、如果一个棱柱共有15条棱,那么它的底面一定是________边形。
15、长方体是一个立体图形,它有________个面,________条棱,________个顶点。
16、六棱柱有________个顶点,________个面,________条棱。
17、如图是由________、长方体、圆柱三种几何体组成的物体。
18、将如图几何体分类,柱体有________,锥体有________,球体有________(填序号)。
19、如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值。
20、(2009春 滨湖区期中)人人争当小小设计师。一个工程队为建设一项重点工程,要在一块长方形荒地上建造几套简易住房,每一套简易住房的平面是由长4y、宽4x构成,要求建成:两室、一厅、一厨、一卫。
其中客厅面积为6xy;两个卧室的面积和为8xy;厨房面积为xy;卫生间面积为xy。请你根据所学知识,在所给图中设计其中一套住房的平面结构示意图。
21、如图,从一个多边形的某一条边上的一点(不与端点重合)出发,分别连接这个点与其他所有顶点,可以把这个多边形分割成若干个三角形,由三角形、四边形、五边形为例,你能总结出什么规律?n边形呢?
22、如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图。
(在图1和图2中任选一个进行解答,只填出一种答案即可)
参考答案
1、【答案】B
【考点】认识立体图形,截一个几何体
【解析】
解:A、用一个平面去截一个圆锥,不可以是椭圆,故选项错误;
B、根据棱柱的特征可知,棱柱的所有侧棱长都相等,故选项正确;
C、用一个平面去截一个圆柱体,截面不可以是梯形,故选项错误;
D、用一个平面去截一个长方体,截面可能是正方形,故选项错误。
故选B。
【分析】根据圆锥、棱柱、圆柱、长方体的形状特点判断即可。
2、【答案】B
【考点】认识立体图形,截一个几何体,简单几何体的三视图
【解析】
解:A、球体的截面一定是圆,故A正确,与要求不符;
B、组成长方体的各面中可能有2个面是正方形,故B错误;
C、从三个不同的方向看正方体,得到的都是正方形,故C正确,与要求不符;
D、圆锥的截面可能是圆,正确,与要求不符。
故选:B。
【分析】根据球体、长方体、正方体、圆锥的形状判断即可。
3、【答案】C
【考点】几何体的展开图
【解析】
解:A、是三棱柱的展开图,故此选项错误;
B、是一个平面图形,故此选项错误;
C、是棱锥的展开图,故此选项正确;
D、是圆柱的展开图,故此选项错误。
故选:C。
【分析】根据图形结合所学的几何体的形状得出即可。
4、【答案】D
【考点】几何体的展开图
【解析】
解:选项A,B,C折叠后,都可以围成一个长方体,而D折叠后,最下面一行的两个面重合,缺少一个底面,所以不能围成一个长方体。
故选D。
【分析】根据图示,进行折叠即可解题。
5、【答案】A
【考点】几何体的展开图
【解析】
解:由分析知:四棱柱的侧面展开图是四个矩形组成的图形。
故选:A。
【分析】根据四棱柱的侧面展开图是矩形图进行解答即可。
6、【答案】C
【考点】几何体的展开图
【解析】
解:A、折叠后不可以组成正方体;
B、折叠后不可以组成正方体;
C、折叠后可以组成正方体;
D、折叠后不可以组成正方体;
故选C。
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解。
7、【答案】B
【考点】几何体的展开图
【解析】
解:观察图形可知,
将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的选项B。
故选:B。
【分析】立体图形的侧面展开图,体现了平面图形与立体图形的联系。
立体图形问题可以转化为平面图形问题解决。
8、【答案】B
【考点】几何体的展开图
【解析】
解:由题意,得
四个小正方形组合成一个正方体的面, 是阴影,
是空白,
故选:B。
【分析】根据展开图折叠成几何体,四个小正方形组合成一个正方体的面,可得答案。
9、【答案】B
【考点】几何体的展开图
【解析】
解:圆锥的侧面展开图是扇形,底面是圆,
故选:B。
【分析】根据圆锥的展开图,可得答案。
10、【答案】B
【考点】几何体的展开图
【解析】
解:由四棱柱四个侧面和上下两个底面的特征可知,A,C,D选项可以拼成一个正方体,而B选项,上底面不可能有两个,故不是正方体的展开图。
故选:B。
【分析】由平面图形的折叠及正方体的展开图解题。
11、【答案】B
【考点】几何体的展开图
【解析】
解:A折叠后不可以组成正方体;B折叠后可以组成正方体;
C折叠后有两个小正方形重合,不符合正方体展开图;
D折叠后不可以组成正方体;
是正方体展开图的是B。
故选B。
【分析】据正方体展开图的11种形式对各小题分析判断即可得解。
12、【答案】A
【考点】几何体的展开图
【解析】
解:因为含小黑正方形的面不能与含大黑正方形的面相邻,两个小黑正方形不能在同一行,所以B,C不是左边展形图的立体图;
两个小黑正方形在大黑正方形的对面”,那么A图中,正好是大黑正方形在上面,那么小黑正方形就在底面,A符合;
故选:A。
【分析】因为含小黑正方形的面不能与含大黑正方形的面相邻,两个小黑正方形不能在同一行,据此判断。
13、【答案】六
【考点】认识立体图形
【解析】
解:7﹣1=6。
故一个棱锥有7个面,这是六棱锥。
故答案为:六。
【分析】求出棱锥的侧面数即为棱锥数。
14、【答案】五
【考点】认识立体图形
【解析】
解:一个棱柱共有15条棱,那么它是五棱柱,
故答案为:五
【分析】根据棱柱的概念和定义,可知有15条棱的棱柱是五棱柱。
15、【答案】6;12;8
【考点】认识立体图形
【解析】
解:长方体有6个面,12条棱,8个顶点。
故答案为:
。
【分析】根据长方体的特征,长方体有6个面,相对的米面积相等;有12条棱互相平行的一组4条棱的长度相等;有8个顶点。
16、【答案】12;8;18
【考点】认识立体图形
【解析】
解:六棱柱上下两个底面是6边形,侧面是6个长方形。
所以共有12个顶点;8个面;18条棱。
故答案为
。
【分析】根据六棱柱的概念和定义即解。
17、【答案】三棱柱
【考点】认识立体图形
【解析】
解:如图是由三棱柱、长方体、圆柱三种几何体组成的物体。
故答案是:三棱柱。
【分析】图示由3种立体图形组成:棱柱、长方体、柱体。
18、【答案】(1)、(2)、(3);(5)、(6);(4)
【考点】认识立体图形
【解析】
解:柱体分为圆柱和棱柱,所以柱体有:(1)、(2)、(3);锥体包括棱锥与圆锥,所以锥体有(5)、(6);球属于单独的一类:球体(4)。
故答案为:(1)、(2)、(3);(5)、(6);(4)
【分析】首先要明确柱体,椎体、球体的概念和定义,然后根据图示进行解答。
19、【答案】解:根据题意得,x﹣3=3x﹣2,
解得:x=﹣
【考点】几何体的展开图
【解析】【分析】利用正方体及其表面展开图的特点,列出方程x﹣3=3x﹣2解答即可。
20、【答案】解:
【考点】认识平面图形
【解析】【分析】根据题意,先计算出客厅、两个卧室、厨房以及卫生间的长与宽分别是多少,再根据长4y、宽4x的平面来设计。
21、【答案】解:由图中可以看出三角形被分为2个三角形;四边形被分为3个三角形,五边形被分为4个三角形,
那么n边形被分为(n﹣1)个三角形。
【考点】认识平面图形
【解析】【分析】由相应图形得到分成的三角形的个数和多边形的边数的关系的规律即可。
22、【答案】解:只写出一种答案即可。
图1:
图2:
【考点】几何体的展开图
【解析】【分析】和一个正方体的平面展开图相比较,可得出一个正方体11种平面展开图。
1、下列说法中,正确的是(
)
A、用一个平面去截一个圆锥,可以是椭圆
B、棱柱的所有侧棱长都相等
C、用一个平面去截一个圆柱体,截面可以是梯形
D、用一个平面去截一个长方体截面不能是正方形
2、下列说法不正确的是(
)
A、球的截面一定是圆
B、组成长方体的各个面中不可能有正方形
C、从三个不同的方向看正方体,得到的都是正方形
D、圆锥的截面可能是圆
3、下列图形中,是棱锥展开图的是(
)
A、
B、
C、
D、
4、下面图形不能围成一个长方体的是(
)
A、
B、
C、
D、
5、下列图形是四棱柱的侧面展开图的是(
)
A、
B、
C、
D、
6、下列图形中,是正方体的表面展开图的是(
)
A、
B、
C、
D、
7、将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的是(
)
A、
B、
C、
D、
8、如图是一个正方体的表面展开图,这个正方体可能是(
)
A、
B、
C、
D、
9、一个几何体的展开图如图所示,这个几何体是(
)
A、棱柱
B、棱锥
C、圆锥
D、圆柱
10、在下面的图形中,不可能是正方体的表面展开图的是(
)
A、
B、
C、
D、
11、下列图形中,是正方体表面展开图的是(
)
A、
B、
C、
D、
12、下列四个图形中是如图展形图的立体图的是(
)
A、
B、
C、
D、
13、一个棱锥有7个面,这是________棱锥。
14、如果一个棱柱共有15条棱,那么它的底面一定是________边形。
15、长方体是一个立体图形,它有________个面,________条棱,________个顶点。
16、六棱柱有________个顶点,________个面,________条棱。
17、如图是由________、长方体、圆柱三种几何体组成的物体。
18、将如图几何体分类,柱体有________,锥体有________,球体有________(填序号)。
19、如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值。
20、(2009春 滨湖区期中)人人争当小小设计师。一个工程队为建设一项重点工程,要在一块长方形荒地上建造几套简易住房,每一套简易住房的平面是由长4y、宽4x构成,要求建成:两室、一厅、一厨、一卫。
其中客厅面积为6xy;两个卧室的面积和为8xy;厨房面积为xy;卫生间面积为xy。请你根据所学知识,在所给图中设计其中一套住房的平面结构示意图。
21、如图,从一个多边形的某一条边上的一点(不与端点重合)出发,分别连接这个点与其他所有顶点,可以把这个多边形分割成若干个三角形,由三角形、四边形、五边形为例,你能总结出什么规律?n边形呢?
22、如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图。
(在图1和图2中任选一个进行解答,只填出一种答案即可)
参考答案
1、【答案】B
【考点】认识立体图形,截一个几何体
【解析】
解:A、用一个平面去截一个圆锥,不可以是椭圆,故选项错误;
B、根据棱柱的特征可知,棱柱的所有侧棱长都相等,故选项正确;
C、用一个平面去截一个圆柱体,截面不可以是梯形,故选项错误;
D、用一个平面去截一个长方体,截面可能是正方形,故选项错误。
故选B。
【分析】根据圆锥、棱柱、圆柱、长方体的形状特点判断即可。
2、【答案】B
【考点】认识立体图形,截一个几何体,简单几何体的三视图
【解析】
解:A、球体的截面一定是圆,故A正确,与要求不符;
B、组成长方体的各面中可能有2个面是正方形,故B错误;
C、从三个不同的方向看正方体,得到的都是正方形,故C正确,与要求不符;
D、圆锥的截面可能是圆,正确,与要求不符。
故选:B。
【分析】根据球体、长方体、正方体、圆锥的形状判断即可。
3、【答案】C
【考点】几何体的展开图
【解析】
解:A、是三棱柱的展开图,故此选项错误;
B、是一个平面图形,故此选项错误;
C、是棱锥的展开图,故此选项正确;
D、是圆柱的展开图,故此选项错误。
故选:C。
【分析】根据图形结合所学的几何体的形状得出即可。
4、【答案】D
【考点】几何体的展开图
【解析】
解:选项A,B,C折叠后,都可以围成一个长方体,而D折叠后,最下面一行的两个面重合,缺少一个底面,所以不能围成一个长方体。
故选D。
【分析】根据图示,进行折叠即可解题。
5、【答案】A
【考点】几何体的展开图
【解析】
解:由分析知:四棱柱的侧面展开图是四个矩形组成的图形。
故选:A。
【分析】根据四棱柱的侧面展开图是矩形图进行解答即可。
6、【答案】C
【考点】几何体的展开图
【解析】
解:A、折叠后不可以组成正方体;
B、折叠后不可以组成正方体;
C、折叠后可以组成正方体;
D、折叠后不可以组成正方体;
故选C。
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解。
7、【答案】B
【考点】几何体的展开图
【解析】
解:观察图形可知,
将选项中的四个正方体分别展开后,所得的平面展开图与如图不同的选项B。
故选:B。
【分析】立体图形的侧面展开图,体现了平面图形与立体图形的联系。
立体图形问题可以转化为平面图形问题解决。
8、【答案】B
【考点】几何体的展开图
【解析】
解:由题意,得
四个小正方形组合成一个正方体的面, 是阴影,
是空白,
故选:B。
【分析】根据展开图折叠成几何体,四个小正方形组合成一个正方体的面,可得答案。
9、【答案】B
【考点】几何体的展开图
【解析】
解:圆锥的侧面展开图是扇形,底面是圆,
故选:B。
【分析】根据圆锥的展开图,可得答案。
10、【答案】B
【考点】几何体的展开图
【解析】
解:由四棱柱四个侧面和上下两个底面的特征可知,A,C,D选项可以拼成一个正方体,而B选项,上底面不可能有两个,故不是正方体的展开图。
故选:B。
【分析】由平面图形的折叠及正方体的展开图解题。
11、【答案】B
【考点】几何体的展开图
【解析】
解:A折叠后不可以组成正方体;B折叠后可以组成正方体;
C折叠后有两个小正方形重合,不符合正方体展开图;
D折叠后不可以组成正方体;
是正方体展开图的是B。
故选B。
【分析】据正方体展开图的11种形式对各小题分析判断即可得解。
12、【答案】A
【考点】几何体的展开图
【解析】
解:因为含小黑正方形的面不能与含大黑正方形的面相邻,两个小黑正方形不能在同一行,所以B,C不是左边展形图的立体图;
两个小黑正方形在大黑正方形的对面”,那么A图中,正好是大黑正方形在上面,那么小黑正方形就在底面,A符合;
故选:A。
【分析】因为含小黑正方形的面不能与含大黑正方形的面相邻,两个小黑正方形不能在同一行,据此判断。
13、【答案】六
【考点】认识立体图形
【解析】
解:7﹣1=6。
故一个棱锥有7个面,这是六棱锥。
故答案为:六。
【分析】求出棱锥的侧面数即为棱锥数。
14、【答案】五
【考点】认识立体图形
【解析】
解:一个棱柱共有15条棱,那么它是五棱柱,
故答案为:五
【分析】根据棱柱的概念和定义,可知有15条棱的棱柱是五棱柱。
15、【答案】6;12;8
【考点】认识立体图形
【解析】
解:长方体有6个面,12条棱,8个顶点。
故答案为:
。
【分析】根据长方体的特征,长方体有6个面,相对的米面积相等;有12条棱互相平行的一组4条棱的长度相等;有8个顶点。
16、【答案】12;8;18
【考点】认识立体图形
【解析】
解:六棱柱上下两个底面是6边形,侧面是6个长方形。
所以共有12个顶点;8个面;18条棱。
故答案为
。
【分析】根据六棱柱的概念和定义即解。
17、【答案】三棱柱
【考点】认识立体图形
【解析】
解:如图是由三棱柱、长方体、圆柱三种几何体组成的物体。
故答案是:三棱柱。
【分析】图示由3种立体图形组成:棱柱、长方体、柱体。
18、【答案】(1)、(2)、(3);(5)、(6);(4)
【考点】认识立体图形
【解析】
解:柱体分为圆柱和棱柱,所以柱体有:(1)、(2)、(3);锥体包括棱锥与圆锥,所以锥体有(5)、(6);球属于单独的一类:球体(4)。
故答案为:(1)、(2)、(3);(5)、(6);(4)
【分析】首先要明确柱体,椎体、球体的概念和定义,然后根据图示进行解答。
19、【答案】解:根据题意得,x﹣3=3x﹣2,
解得:x=﹣
【考点】几何体的展开图
【解析】【分析】利用正方体及其表面展开图的特点,列出方程x﹣3=3x﹣2解答即可。
20、【答案】解:
【考点】认识平面图形
【解析】【分析】根据题意,先计算出客厅、两个卧室、厨房以及卫生间的长与宽分别是多少,再根据长4y、宽4x的平面来设计。
21、【答案】解:由图中可以看出三角形被分为2个三角形;四边形被分为3个三角形,五边形被分为4个三角形,
那么n边形被分为(n﹣1)个三角形。
【考点】认识平面图形
【解析】【分析】由相应图形得到分成的三角形的个数和多边形的边数的关系的规律即可。
22、【答案】解:只写出一种答案即可。
图1:
图2:
【考点】几何体的展开图
【解析】【分析】和一个正方体的平面展开图相比较,可得出一个正方体11种平面展开图。
