21.2.4 一元二次方程的根与系数的关系课件
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-15 11:32:27 | ||
图片预览






文档简介
课件14张PPT。 第二十一章 一元二次方程21.2.4 一元二次方程的根与系数的关系九年级数学上 新课标 [人]问题思考 我们知道生活中许多事物存在着一定的规律,有人发现并验证后就得到伟大的定理,比如, 抛出的重物总会落下—万有引力定律(牛顿);电路中的电流、电压、电阻存在一定关系:U=IR—欧姆定律(欧姆).而我们数学学科中更蕴藏着大量的规律. 比如,直角三角形的三边a,b,c满足关系: a2+b2=c2—勾股定理(毕达哥拉斯定理).那么一元二次方程中是否也存在什么规律呢?探究活动一观察表格,思考问题.
(1)通过观察,你发现什么规律?
(2)语言叙述你发现的规律.
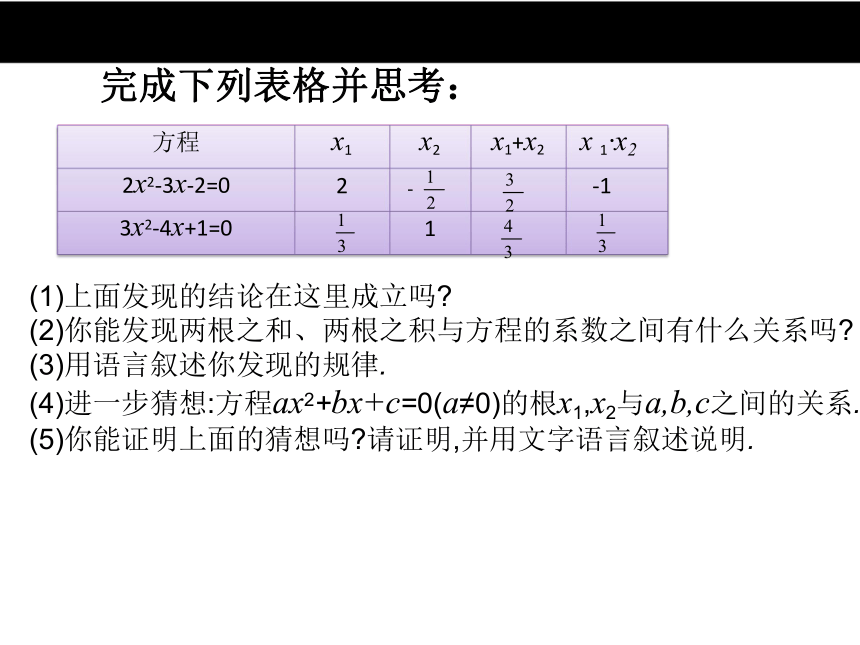
(3)设x2+px+q=0的两根为x1,x2,用式子表示你 发现的规律.方程x2+px+q=0的两根为x1,x2,则x1+x2=-p,x1x2=q.(1)上面发现的结论在这里成立吗?
(2)你能发现两根之和、两根之积与方程的系数之间有什么关系吗?
(3)用语言叙述你发现的规律.
(4)进一步猜想:方程ax2+bx+c=0(a≠0)的根x1,x2与a,b,c之间的关系.
(5)你能证明上面的猜想吗?请证明,并用文字语言叙述说明.
完成下列表格并思考:探究活动二根据求根公式,得归纳总结
1.一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比;
2.一元二次方程的根与系数之间的关系(韦达定理);
3.一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2 ,x1x2
例题讲解(教材例4)根据一元二次方程的根与系
数的关系,求下列方程两个根x1,x2的和与积:
(1)x2-6x-15=0;
(2)3x2+7x-9=0;
(3)5x-1=4x2.
?答案知识拓展1.根与系数之间的关系在方程ax2+bx+c=0(a≠0)有根的前提下(b2-4ac≥0)才能够成立,运用根与系数的关系解题时首先要检验b2-4ac是否非负..∴ x1=.2.利用根与系数之间的关系可以不解方程而求出与根有关的代数式的值.比如课堂小结在方程ax2+bx+c=0(a≠0)中a,b,c的作用:
1.二次项系数a是否为零,决定着方程是否为二次方程;
2 .当a≠0时,Δ=b2-4ac可判定根的情况;
1.若x1,x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是 ( )
A.-10 B.10 C.-16 D.16解析:考查根与系数之间的关系若x1,x2是一元二次方程x2+10x+16=0的两个根,则x1+x2=-10.故选A.A2.一元二次方程x2+x-2=0的两根之积是 ( )
A.-1 B.-2 C.1 D.2
解析:设方程的两个根为x1,x2,根据根与系数之间的关系可得x1x2= = -2.故选B.B3.已知方程x2-5x+2=0的两个解分别为x1,x2,则x1+x2-x1·x2的值为 ( )
A.-7 B.-3 C.7 D.34.方程x2=2x-1的两根之和等于 .?解析:将方程化简可得x2-2x+1=0,设方程的两个根为x1,x2,根据根与系数之间的关系可得解析:根据根与系数之间的关系可得x1+x2= =5,x1x2= =2,所以x1+x2-x1·x2=5-2=3.故选D.D25.已知方程x2-6x-2m+5=0的一个根为2,
求另一个根及m的值..,解:设方程的两个根为x1,x2,根据根与系数之间
的关系可得∵方程的一个根为2,
∴方程的另一个根为4,且-2m+5=8,6.已知关于x的一元二次方程5x2-4x-1=0的两个解为x1和x2.
解:(1)由方程根与系数之间的关系得
(1)通过观察,你发现什么规律?
(2)语言叙述你发现的规律.
(3)设x2+px+q=0的两根为x1,x2,用式子表示你 发现的规律.方程x2+px+q=0的两根为x1,x2,则x1+x2=-p,x1x2=q.(1)上面发现的结论在这里成立吗?
(2)你能发现两根之和、两根之积与方程的系数之间有什么关系吗?
(3)用语言叙述你发现的规律.
(4)进一步猜想:方程ax2+bx+c=0(a≠0)的根x1,x2与a,b,c之间的关系.
(5)你能证明上面的猜想吗?请证明,并用文字语言叙述说明.
完成下列表格并思考:探究活动二根据求根公式,得归纳总结
1.一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比;
2.一元二次方程的根与系数之间的关系(韦达定理);
3.一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2 ,x1x2
例题讲解(教材例4)根据一元二次方程的根与系
数的关系,求下列方程两个根x1,x2的和与积:
(1)x2-6x-15=0;
(2)3x2+7x-9=0;
(3)5x-1=4x2.
?答案知识拓展1.根与系数之间的关系在方程ax2+bx+c=0(a≠0)有根的前提下(b2-4ac≥0)才能够成立,运用根与系数的关系解题时首先要检验b2-4ac是否非负..∴ x1=.2.利用根与系数之间的关系可以不解方程而求出与根有关的代数式的值.比如课堂小结在方程ax2+bx+c=0(a≠0)中a,b,c的作用:
1.二次项系数a是否为零,决定着方程是否为二次方程;
2 .当a≠0时,Δ=b2-4ac可判定根的情况;
1.若x1,x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是 ( )
A.-10 B.10 C.-16 D.16解析:考查根与系数之间的关系若x1,x2是一元二次方程x2+10x+16=0的两个根,则x1+x2=-10.故选A.A2.一元二次方程x2+x-2=0的两根之积是 ( )
A.-1 B.-2 C.1 D.2
解析:设方程的两个根为x1,x2,根据根与系数之间的关系可得x1x2= = -2.故选B.B3.已知方程x2-5x+2=0的两个解分别为x1,x2,则x1+x2-x1·x2的值为 ( )
A.-7 B.-3 C.7 D.34.方程x2=2x-1的两根之和等于 .?解析:将方程化简可得x2-2x+1=0,设方程的两个根为x1,x2,根据根与系数之间的关系可得解析:根据根与系数之间的关系可得x1+x2= =5,x1x2= =2,所以x1+x2-x1·x2=5-2=3.故选D.D25.已知方程x2-6x-2m+5=0的一个根为2,
求另一个根及m的值..,解:设方程的两个根为x1,x2,根据根与系数之间
的关系可得∵方程的一个根为2,
∴方程的另一个根为4,且-2m+5=8,6.已知关于x的一元二次方程5x2-4x-1=0的两个解为x1和x2.
解:(1)由方程根与系数之间的关系得
同课章节目录
