22.3 实际问题与二次函数课件
图片预览








文档简介
(共54张PPT)
(1)利用已知点的坐标,求出抛物线的解析式:
当已知三个点的坐标时,可用一般式y=ax2+bx+c(a≠0)求其解析式;
当已知顶点坐标为(k,h)和另外一点的坐标时,可用顶点式
求其解析式;
当已知抛物线与x轴的两个交点坐标分别为(x1,0),(x2,0)时,可用交点式 求其解析式.
(2)对于任意一个二次函数的一般式y=ax2+bx+c(a≠0),可以利用配方把它化为顶点式,进而写出顶点坐标和对称轴.
(3)求二次函数y=ax2+bx+c(a≠0)与x轴的交点,即令y=0即可;其与x轴交点即为(x1,0)、(x2,0); 求二次函数y=ax2+bx+c(a≠0)与y轴的交点,即令x=0即可;其与y轴交点即为(0,c).
(4)将二次函数的一般式转化成顶点式来求二次函数最值.
创设情境 明确目标
自主学习 指向目标
2.会运用二次函数知识解决其他简单的实际问题.
1.会建立恰当的平面直角坐标系,构建二次函
数模型,解决抛物线拱桥问题.
合作探究 达成目标
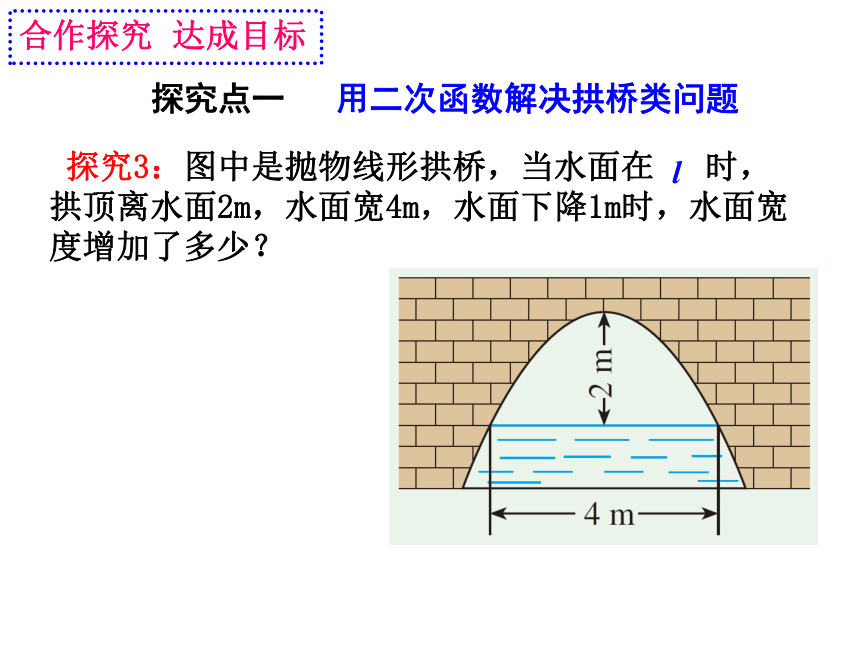
探究点一 用二次函数解决拱桥类问题
探究3:图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
阅读教材P51探究3,完成下列填空:
1. 以拱桥的顶点为原点,以经过该点的铅垂线为y轴建立平面直角坐标系时,可设这条抛物线的关系式为___________.
2. 一座拱桥为抛物线形,其函数解析式为__________,
当水位线在AB位置时,水面宽4 m,这时水面离桥顶的高度为_____m;当桥拱顶点到水面距离为2 m时,水面宽为_____m,A点坐标为______________,B点坐标为_____________,
则函数解析式为_______________.
探究一:利用二次函数解决抛物线形拱桥问题
活动2
自学互研,生成能力
重点知识★
4
2
(-2,-2)
(2,-2)
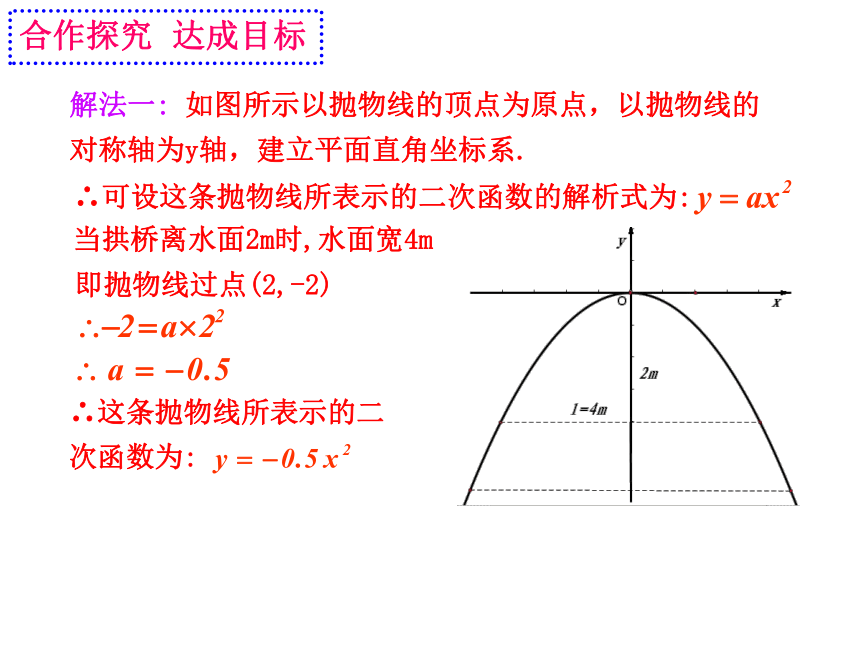
解法一: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
合作探究 达成目标
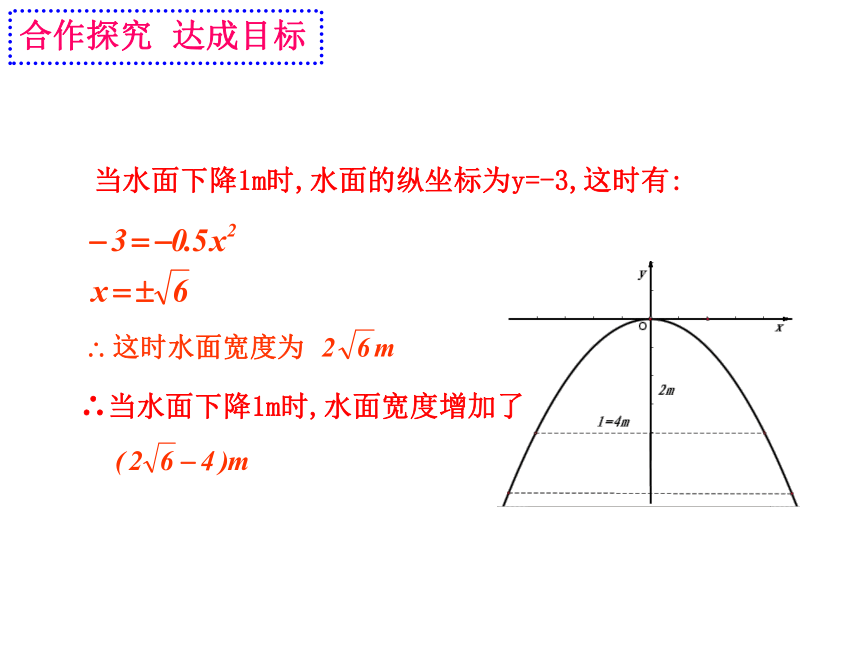
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
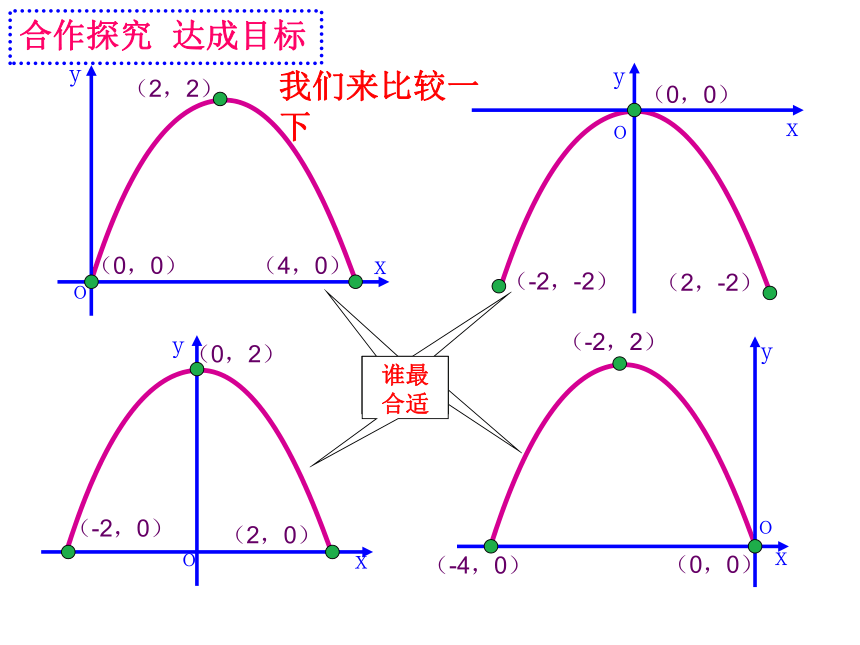
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最合适
y
y
y
y
o
o
o
o
x
x
x
x
合作探究 达成目标
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的
二次函数的解析式为:
此时,抛物线的顶点为(0,2)
合作探究 达成目标
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
∵抛物线过点(0,0)
∴这条抛物线所表示的二次函数为:
此时,抛物线的顶点为(2,2)
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
∴这时水面的宽度为:
合作探究 达成目标
1.理解问题;
回顾上一节“最大利润”和本节“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?
2.分析问题中的变量和常量,以及它们之间的关系
3.用数学的方式表示出它们之间的关系;
4.用数学求解;
5.检验结果的合理性
“二次函数应用”的思路
合作探究 达成目标
1.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是___________.
2.在上题中,若水面下降,宽度变为2米,此时水面离涵洞顶点的距离为_______米。
例、小明在某次投篮中,球的运动路线是抛物线 的一部分,如图所示,若命中篮圈中心,则他与篮底的距离L是多少?
探究二:建立二次函数模型,解决其它实际问题
解:当y=3.05时, +3.5=3.05
解得:
所以 L=3+1.5=4.5
则他与篮底的距离L是4.5m.
合作探究 达成目标
探究点二 用二次函数解决生活中的实际问题
例:飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数关系式是s=60t-1.5t2 ,飞机着陆后滑行多少秒才能停下来?
思考:飞机从着陆的一瞬间开始计时,到滑行到最远距离停下来所用的时间即为所求,也就是使S取得什么值时的t的值?
解: s=60t-1.5t2
=-1.5(t-20)2+600
∴当t=20时,s最大,此时飞机才能停下来。
抽象
转化
数学问题
运用
数学知识
问题的解决
解题步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
实际问题
合作探究 达成目标
探究点二 用二次函数解决生活中的实际问题
600
飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数关系式是s=60t-1.5t2 ,飞机着陆后滑行_________m才能停下来.
总结梳理 内化目标
达标检测 反思目标
D
B
y=-2x2
练习2. 某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,求校门的高.(精确到0.1米,水泥建筑物厚度忽略不计)
【思路点拨】先建立坐标系,然后根据线段的长度写出点的坐标,再设出函数的解析式,利用点的坐标求出解析式.
探究三:利用二次函数解决实际问题的训练
解:以大门的地面为x轴,大门的正中间为y轴建立直角坐标系,
由题意可知抛物线过(-4,0),(4,0),(-3,4)三点.
∵ 抛物线关于y轴对称,
可设解析式为y=ax2+c,
则
解得
所以抛物线的函数解析式为
∴ 顶点坐标为(0, ),
则校门的高为 ≈9.1(米)
探究三:利用二次函数解决实际问题的训练
达标检测 反思目标
102
练习. 有一抛物线形拱桥,其最大高度为16米,跨度为40米,把它的示意图放在如图所示的坐标系中,则抛物线的函数关系式为_________________ .
解:因为抛物线过点(0,0)和(40,0),
∴ y=ax(x- 40)①
又∵ 函数过点(20,16)代入①得20a(20-40)=16,
解得
∴ 抛物线的解析式为 .
探究三:利用二次函数解决实际问题的训练
例2. 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).
问:此船能否顺利通过这座拱桥?
【思路点拨】
(1)以拱桥最顶端为原点,建立直角坐标系,根据题目中所给的数据写出函数解析式.
(2)先求x=3米时y的值,用拱桥最大高度减去|y|,然后与3.6相比较即可得出答案.
探究三:利用二次函数解决实际问题的训练
解:(1)设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
n=10 a=100a,n+3=5 a=25a,
(2)∵ 货轮经过拱桥时的横坐标为x=3,
∴ 当x=3时,
∴ 在正常水位时,此船能顺利通过这座拱桥.
即
解得
探究三:利用二次函数解决实际问题的训练
练习. 如图,有一座抛物线形拱桥,桥下面在正常水位AB时宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)建立如图的坐标系,求抛物线的函数解析式;
(2)若洪水到来时水位以0.2 m/h的速度上升,从正常水位开始,再过几小时就能到达桥面?
解:(1)由题意知点D的横坐标为5,点B的横坐标为10,EF=3,
设OE=h,则OF=h-3,则点B(10,-h),D(5,3-h).
设抛物线的函数解析式为y=ax2,
探究三:利用二次函数解决实际问题的训练
(2) ∵B(10,-4),
∴ 拱桥顶O到CD的距离为4,
∴ 小时.
所以再过20 h就能到达桥面.
则
解得
所以抛物线的函数解析式为
探究三:利用二次函数解决实际问题的训练
例3.在一次羽毛球赛中,甲运动员在离地面 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0)
(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
探究三:利用二次函数解决实际问题的训练
活动2
提升型例题
【思路点拨】
(1)设抛物线解析式为y=a(x﹣5)2+3,将点(0, )代入可得出a的值,继而得出抛物线解析式.
(2)令y=0,可得出ON的长度,由NC=ON﹣OC即可得出答案.
(3)先计算出刚好接到球时m的值,从而结合所给图形可得出运动员接球高度不够m的取值范围.
探究三:利用二次函数解决实际问题的训练
解:(1)设抛物线解析式为y=a(x-5)2+3,将点(0, )代入
可得:
(2)当y=0时,
解得:
故抛物线的解析式为:
解得:
即
∵ OC=6
∴ CN=
探究三:利用二次函数解决实际问题的训练
(3)若运动员乙原地起跳到最大高度时刚好接到球,
此时
解得:m1=2,m2=8,
∵ 运动员接球高度不够,
∴ 2<m<8,
∵ OC=6,乙运动员接球时不能触网(接不到),
∴ m的取值范围为:6<m<8.
探究三:利用二次函数解决实际问题的训练
练习. 火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式 表示.经过_______s,火箭达到它的最高点.
【思路点拨】可以把题目所给的一般式化为顶点式直接求解;
【解题过程】解:配方可得 ,
因此当t=15秒时火箭达到最高点.
15
探究三:利用二次函数解决实际问题的训练
例4.某桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为x轴,经过抛物线的顶点C与x轴垂直的直线为y轴,建立平面直角坐标系.已知此桥垂直于桥面的相邻两柱之间距离为2m(图中用线段AD、CO、BE等表示桥柱),CO=1m,FG=2m.
(1)求经过A、B、C三点的抛物线相应的二次函数关系式;
(2)求柱子AD的高度.
探究三:利用二次函数解决实际问题的训练
(2)因为点A的横坐标为-8,当x=-8时,y=5.
所以柱子AD的高度为5米.
解:(1)由题意可知:点C坐标为(0,1),点F坐标为(-4,2),设抛物线解析式为y=ax2+c,把这两个点代入函数解析式可以解得抛物线解析式y= x2+1.
(1)求经过A、B、C三点的抛物线相应的二次函数关系式;
(2)求柱子AD的高度.
探究三:利用二次函数解决实际问题的训练
例5.如图1,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(NC=4.5米).当水位上涨刚好淹没小孔时,借助图2中的直角坐标系,求此时大孔的水面宽度EF.
探究三:利用二次函数解决实际问题的训练
活动3
探究型例题
图1
图2
【思路点拨】根据线段的长度写出相关点的坐标,再设出函数的解析式,把点的坐标代入解析式求出解析式,可以算出EF的宽度.
依题意,得B(10,0).
∴ a×10 +6=0.
解得a=-0.06.
即
解:设大孔对应的抛物线所对应的函数关系式为
∴DF=5,EF=10.
即水面宽度为10米.
当y=4.5时, ,解得
例5.如图1,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(NC=4.5米).当水位上涨刚好淹没小孔时,借助图2中的直角坐标系,求此时大孔的水面宽度EF.
探究三:利用二次函数解决实际问题的训练
练习. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;
(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由.
探究三:利用二次函数解决实际问题的训练
解:(1)设抛物线对应的函数关系式为
因为抛物线的顶点为原点,隧道宽6m,高5m,矩形的高为2m,
所以抛物线过点A(-3,-3),
代入得-3=9a,解得
所以函数关系式为
练习. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;
探究三:利用二次函数解决实际问题的训练
解:(2)如果此车能通过隧道,集装箱处于对称位置,
将x=1.5代入抛物线方程,得y=-0.75,
此时集装箱角离隧道的底为5-0.75=4.25米,不及车与箱总高4.5米,
即4.25<4.5,从而此车不能通过此隧道.
练习. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由.
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围)
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,她起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围)
解: (1)根据题意知此时抛物线的顶点G的坐标为(7,3.2),
设抛物线解析式为y=a(x-7)2+3.2
将点C(0,1.8)代入得49a+3.2=1.8,
解得
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,她起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
解:(2)由题意当x=9.5时,
故这次她可以拦网成功.
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
解:(3)设抛物线解析式为y=a(x-7)2+h,将点C(0,1.8)代入得49a+h=1.8,
由题意得
解得
则排球飞行的最大高度h的取值范围是h≥3.025.
探究三:利用二次函数解决实际问题的训练
如图,排球运动员站在点O处练习发球,将球从O点正上方2米的C处发出,把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6) +h。已知球网AB与O点的水平距离为9米,高度为2.43米,球场的边界D距离O点18米。
(1)当h=2.6时,求y与x的关系式。
(2)当h=2.6时,球能否过网?会不会出界?说明理由。
(3)若球一定能越过球网,又不出边界,求h的取值范围。
(1)
(2)当x=9时,y=2.45>2.43,所以能过网;当y=0时,
(3)当球正好过(18,0)时,抛物线还过点(0,2),代入解析式得
当球正好能过网,此时抛物线过(9,2.43),还过点(0,2),代入解析得
练习. 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由
解:(1)配方得
当x= 时,y有最大值 ,
∴ 演员弹跳离地面的最大高度是4.75米.
探究三:利用二次函数解决实际问题的训练
练习. 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由
解:(2)表演成功.
理由:把x=4代入解析式得y=3.4,
即点B(4,3.4)在抛物线 上,所以表演成功.
探究三:利用二次函数解决实际问题的训练
知识梳理
1. 解拱桥问题、投球时球的运动轨迹、弹道轨迹、跳水时人体的运动轨迹的二次函数应用问题时,一般分为以下五个步骤:
(1)建立适当的直角坐标系(若题目中给出,不用重建);
(2)确定解析式的类型,若顶点在原点上,一般设二次函数的解析式为y=ax2 ;若顶点不在原点上,一般设二次函数的解析式为y=ax2+k;
(3)根据给定的条件,找出抛物线上已知的点,并写出坐标;
(4)利用已知点的坐标,求出抛物线的解析式:
当已知三个点的坐标时,可用一般式y=ax2+bx+c(a≠0)求其解析式;
知识梳理
当已知顶点坐标为(k,h)和另外一点的坐标时,可用顶点式
求其解析式;
当已知抛物线与x轴的两个交点坐标分别为(x1,0),(x2,0)时,可用交点式 求其解析式.
(5)利用抛物线解析式求出与问题相关的点的坐标,从而使问题获解.
2. 建立坐标系之后,根据线段的长度写出点的坐标,把点的坐标代入到相关的解析式中求出解析式,利用解析式求解相关问题.
重难点归纳
1.根据实际问题,建立适当的直角坐标系.
2.根据给定的条件,确定二次函数的解析式,求出与问题相关的点的坐标.
3.数形结合思想特别重要,在思考的过程中需要结合题意画出满足条件的图形,尤其是动态问题中画出图形是解题的关键.
上交作业:教科书第42页第11.12题 .
课后作业:“学生用书”的“课后作业”部分.
(1)利用已知点的坐标,求出抛物线的解析式:
当已知三个点的坐标时,可用一般式y=ax2+bx+c(a≠0)求其解析式;
当已知顶点坐标为(k,h)和另外一点的坐标时,可用顶点式
求其解析式;
当已知抛物线与x轴的两个交点坐标分别为(x1,0),(x2,0)时,可用交点式 求其解析式.
(2)对于任意一个二次函数的一般式y=ax2+bx+c(a≠0),可以利用配方把它化为顶点式,进而写出顶点坐标和对称轴.
(3)求二次函数y=ax2+bx+c(a≠0)与x轴的交点,即令y=0即可;其与x轴交点即为(x1,0)、(x2,0); 求二次函数y=ax2+bx+c(a≠0)与y轴的交点,即令x=0即可;其与y轴交点即为(0,c).
(4)将二次函数的一般式转化成顶点式来求二次函数最值.
创设情境 明确目标
自主学习 指向目标
2.会运用二次函数知识解决其他简单的实际问题.
1.会建立恰当的平面直角坐标系,构建二次函
数模型,解决抛物线拱桥问题.
合作探究 达成目标
探究点一 用二次函数解决拱桥类问题
探究3:图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
阅读教材P51探究3,完成下列填空:
1. 以拱桥的顶点为原点,以经过该点的铅垂线为y轴建立平面直角坐标系时,可设这条抛物线的关系式为___________.
2. 一座拱桥为抛物线形,其函数解析式为__________,
当水位线在AB位置时,水面宽4 m,这时水面离桥顶的高度为_____m;当桥拱顶点到水面距离为2 m时,水面宽为_____m,A点坐标为______________,B点坐标为_____________,
则函数解析式为_______________.
探究一:利用二次函数解决抛物线形拱桥问题
活动2
自学互研,生成能力
重点知识★
4
2
(-2,-2)
(2,-2)
解法一: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最合适
y
y
y
y
o
o
o
o
x
x
x
x
合作探究 达成目标
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的
二次函数的解析式为:
此时,抛物线的顶点为(0,2)
合作探究 达成目标
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
∵抛物线过点(0,0)
∴这条抛物线所表示的二次函数为:
此时,抛物线的顶点为(2,2)
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
∴这时水面的宽度为:
合作探究 达成目标
1.理解问题;
回顾上一节“最大利润”和本节“桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?
2.分析问题中的变量和常量,以及它们之间的关系
3.用数学的方式表示出它们之间的关系;
4.用数学求解;
5.检验结果的合理性
“二次函数应用”的思路
合作探究 达成目标
1.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是___________.
2.在上题中,若水面下降,宽度变为2米,此时水面离涵洞顶点的距离为_______米。
例、小明在某次投篮中,球的运动路线是抛物线 的一部分,如图所示,若命中篮圈中心,则他与篮底的距离L是多少?
探究二:建立二次函数模型,解决其它实际问题
解:当y=3.05时, +3.5=3.05
解得:
所以 L=3+1.5=4.5
则他与篮底的距离L是4.5m.
合作探究 达成目标
探究点二 用二次函数解决生活中的实际问题
例:飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数关系式是s=60t-1.5t2 ,飞机着陆后滑行多少秒才能停下来?
思考:飞机从着陆的一瞬间开始计时,到滑行到最远距离停下来所用的时间即为所求,也就是使S取得什么值时的t的值?
解: s=60t-1.5t2
=-1.5(t-20)2+600
∴当t=20时,s最大,此时飞机才能停下来。
抽象
转化
数学问题
运用
数学知识
问题的解决
解题步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的解析式求解.
4.根据二次函数的解析式解决具体的实际问题.
实际问题
合作探究 达成目标
探究点二 用二次函数解决生活中的实际问题
600
飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数关系式是s=60t-1.5t2 ,飞机着陆后滑行_________m才能停下来.
总结梳理 内化目标
达标检测 反思目标
D
B
y=-2x2
练习2. 某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,求校门的高.(精确到0.1米,水泥建筑物厚度忽略不计)
【思路点拨】先建立坐标系,然后根据线段的长度写出点的坐标,再设出函数的解析式,利用点的坐标求出解析式.
探究三:利用二次函数解决实际问题的训练
解:以大门的地面为x轴,大门的正中间为y轴建立直角坐标系,
由题意可知抛物线过(-4,0),(4,0),(-3,4)三点.
∵ 抛物线关于y轴对称,
可设解析式为y=ax2+c,
则
解得
所以抛物线的函数解析式为
∴ 顶点坐标为(0, ),
则校门的高为 ≈9.1(米)
探究三:利用二次函数解决实际问题的训练
达标检测 反思目标
102
练习. 有一抛物线形拱桥,其最大高度为16米,跨度为40米,把它的示意图放在如图所示的坐标系中,则抛物线的函数关系式为_________________ .
解:因为抛物线过点(0,0)和(40,0),
∴ y=ax(x- 40)①
又∵ 函数过点(20,16)代入①得20a(20-40)=16,
解得
∴ 抛物线的解析式为 .
探究三:利用二次函数解决实际问题的训练
例2. 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).
问:此船能否顺利通过这座拱桥?
【思路点拨】
(1)以拱桥最顶端为原点,建立直角坐标系,根据题目中所给的数据写出函数解析式.
(2)先求x=3米时y的值,用拱桥最大高度减去|y|,然后与3.6相比较即可得出答案.
探究三:利用二次函数解决实际问题的训练
解:(1)设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,
设点B(10,n),点D(5,n+3),
n=10 a=100a,n+3=5 a=25a,
(2)∵ 货轮经过拱桥时的横坐标为x=3,
∴ 当x=3时,
∴ 在正常水位时,此船能顺利通过这座拱桥.
即
解得
探究三:利用二次函数解决实际问题的训练
练习. 如图,有一座抛物线形拱桥,桥下面在正常水位AB时宽20 m,水位上升3 m就达到警戒线CD,这时水面宽度为10 m.
(1)建立如图的坐标系,求抛物线的函数解析式;
(2)若洪水到来时水位以0.2 m/h的速度上升,从正常水位开始,再过几小时就能到达桥面?
解:(1)由题意知点D的横坐标为5,点B的横坐标为10,EF=3,
设OE=h,则OF=h-3,则点B(10,-h),D(5,3-h).
设抛物线的函数解析式为y=ax2,
探究三:利用二次函数解决实际问题的训练
(2) ∵B(10,-4),
∴ 拱桥顶O到CD的距离为4,
∴ 小时.
所以再过20 h就能到达桥面.
则
解得
所以抛物线的函数解析式为
探究三:利用二次函数解决实际问题的训练
例3.在一次羽毛球赛中,甲运动员在离地面 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0)
(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
探究三:利用二次函数解决实际问题的训练
活动2
提升型例题
【思路点拨】
(1)设抛物线解析式为y=a(x﹣5)2+3,将点(0, )代入可得出a的值,继而得出抛物线解析式.
(2)令y=0,可得出ON的长度,由NC=ON﹣OC即可得出答案.
(3)先计算出刚好接到球时m的值,从而结合所给图形可得出运动员接球高度不够m的取值范围.
探究三:利用二次函数解决实际问题的训练
解:(1)设抛物线解析式为y=a(x-5)2+3,将点(0, )代入
可得:
(2)当y=0时,
解得:
故抛物线的解析式为:
解得:
即
∵ OC=6
∴ CN=
探究三:利用二次函数解决实际问题的训练
(3)若运动员乙原地起跳到最大高度时刚好接到球,
此时
解得:m1=2,m2=8,
∵ 运动员接球高度不够,
∴ 2<m<8,
∵ OC=6,乙运动员接球时不能触网(接不到),
∴ m的取值范围为:6<m<8.
探究三:利用二次函数解决实际问题的训练
练习. 火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式 表示.经过_______s,火箭达到它的最高点.
【思路点拨】可以把题目所给的一般式化为顶点式直接求解;
【解题过程】解:配方可得 ,
因此当t=15秒时火箭达到最高点.
15
探究三:利用二次函数解决实际问题的训练
例4.某桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为x轴,经过抛物线的顶点C与x轴垂直的直线为y轴,建立平面直角坐标系.已知此桥垂直于桥面的相邻两柱之间距离为2m(图中用线段AD、CO、BE等表示桥柱),CO=1m,FG=2m.
(1)求经过A、B、C三点的抛物线相应的二次函数关系式;
(2)求柱子AD的高度.
探究三:利用二次函数解决实际问题的训练
(2)因为点A的横坐标为-8,当x=-8时,y=5.
所以柱子AD的高度为5米.
解:(1)由题意可知:点C坐标为(0,1),点F坐标为(-4,2),设抛物线解析式为y=ax2+c,把这两个点代入函数解析式可以解得抛物线解析式y= x2+1.
(1)求经过A、B、C三点的抛物线相应的二次函数关系式;
(2)求柱子AD的高度.
探究三:利用二次函数解决实际问题的训练
例5.如图1,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(NC=4.5米).当水位上涨刚好淹没小孔时,借助图2中的直角坐标系,求此时大孔的水面宽度EF.
探究三:利用二次函数解决实际问题的训练
活动3
探究型例题
图1
图2
【思路点拨】根据线段的长度写出相关点的坐标,再设出函数的解析式,把点的坐标代入解析式求出解析式,可以算出EF的宽度.
依题意,得B(10,0).
∴ a×10 +6=0.
解得a=-0.06.
即
解:设大孔对应的抛物线所对应的函数关系式为
∴DF=5,EF=10.
即水面宽度为10米.
当y=4.5时, ,解得
例5.如图1,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(NC=4.5米).当水位上涨刚好淹没小孔时,借助图2中的直角坐标系,求此时大孔的水面宽度EF.
探究三:利用二次函数解决实际问题的训练
练习. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;
(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由.
探究三:利用二次函数解决实际问题的训练
解:(1)设抛物线对应的函数关系式为
因为抛物线的顶点为原点,隧道宽6m,高5m,矩形的高为2m,
所以抛物线过点A(-3,-3),
代入得-3=9a,解得
所以函数关系式为
练习. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;
探究三:利用二次函数解决实际问题的训练
解:(2)如果此车能通过隧道,集装箱处于对称位置,
将x=1.5代入抛物线方程,得y=-0.75,
此时集装箱角离隧道的底为5-0.75=4.25米,不及车与箱总高4.5米,
即4.25<4.5,从而此车不能通过此隧道.
练习. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
(2)某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由.
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围)
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,她起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围)
解: (1)根据题意知此时抛物线的顶点G的坐标为(7,3.2),
设抛物线解析式为y=a(x-7)2+3.2
将点C(0,1.8)代入得49a+3.2=1.8,
解得
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,她起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
解:(2)由题意当x=9.5时,
故这次她可以拦网成功.
探究三:利用二次函数解决实际问题的训练
例6.为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G,建立如图所示的平面直角坐标系.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
解:(3)设抛物线解析式为y=a(x-7)2+h,将点C(0,1.8)代入得49a+h=1.8,
由题意得
解得
则排球飞行的最大高度h的取值范围是h≥3.025.
探究三:利用二次函数解决实际问题的训练
如图,排球运动员站在点O处练习发球,将球从O点正上方2米的C处发出,把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6) +h。已知球网AB与O点的水平距离为9米,高度为2.43米,球场的边界D距离O点18米。
(1)当h=2.6时,求y与x的关系式。
(2)当h=2.6时,球能否过网?会不会出界?说明理由。
(3)若球一定能越过球网,又不出边界,求h的取值范围。
(1)
(2)当x=9时,y=2.45>2.43,所以能过网;当y=0时,
(3)当球正好过(18,0)时,抛物线还过点(0,2),代入解析式得
当球正好能过网,此时抛物线过(9,2.43),还过点(0,2),代入解析得
练习. 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由
解:(1)配方得
当x= 时,y有最大值 ,
∴ 演员弹跳离地面的最大高度是4.75米.
探究三:利用二次函数解决实际问题的训练
练习. 如图,杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由
解:(2)表演成功.
理由:把x=4代入解析式得y=3.4,
即点B(4,3.4)在抛物线 上,所以表演成功.
探究三:利用二次函数解决实际问题的训练
知识梳理
1. 解拱桥问题、投球时球的运动轨迹、弹道轨迹、跳水时人体的运动轨迹的二次函数应用问题时,一般分为以下五个步骤:
(1)建立适当的直角坐标系(若题目中给出,不用重建);
(2)确定解析式的类型,若顶点在原点上,一般设二次函数的解析式为y=ax2 ;若顶点不在原点上,一般设二次函数的解析式为y=ax2+k;
(3)根据给定的条件,找出抛物线上已知的点,并写出坐标;
(4)利用已知点的坐标,求出抛物线的解析式:
当已知三个点的坐标时,可用一般式y=ax2+bx+c(a≠0)求其解析式;
知识梳理
当已知顶点坐标为(k,h)和另外一点的坐标时,可用顶点式
求其解析式;
当已知抛物线与x轴的两个交点坐标分别为(x1,0),(x2,0)时,可用交点式 求其解析式.
(5)利用抛物线解析式求出与问题相关的点的坐标,从而使问题获解.
2. 建立坐标系之后,根据线段的长度写出点的坐标,把点的坐标代入到相关的解析式中求出解析式,利用解析式求解相关问题.
重难点归纳
1.根据实际问题,建立适当的直角坐标系.
2.根据给定的条件,确定二次函数的解析式,求出与问题相关的点的坐标.
3.数形结合思想特别重要,在思考的过程中需要结合题意画出满足条件的图形,尤其是动态问题中画出图形是解题的关键.
上交作业:教科书第42页第11.12题 .
课后作业:“学生用书”的“课后作业”部分.
同课章节目录
