第三章 圆单元检测A卷
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
圆单元检测A卷
姓名:__________班级:__________考号:__________
1 、选择题(本大题共12小题 )
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
( http: / / www.21cnjy.com )
A.5 B.7 C.9 D.11
如图,AB是⊙O的直径, ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),∠COD=34°,则∠AEO的度数是( )
( http: / / www.21cnjy.com )
A.51° B.56° C.68° D.78°
如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
( http: / / www.21cnjy.com )
A.75° B.60° C.45° D.30°
如图,四边形ABCD内接于⊙O,E是CB的延长线上一点,∠EBA=125°,则∠D=( )
( http: / / www.21cnjy.com )
A.65° B.120° C.125° D.130°
下列说法正确的是( )
A.同圆或等圆中弧相等,则它们所对的圆心角也相等
B.90°的圆心角所对的弦是直径
C.平分弦的直径垂直于这条弦
D.三点确定一个圆
已知☉O的半径为6,A为线段PO的中点,当OP=10时,点A与☉O的位置关系为( )
A.在圆上 B.在圆外 C.在圆内 D.不确定
点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100° C.40°或140° D.40°或100°
圆最长弦为12cm,如果直线与圆相交,且直线与圆心的距离为d,那么( )
A.d<6cm B.6cm12cm
如图,AB是⊙O的弦,AC是⊙Or切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )21cnjy.com
A.20° B.25° C. 40° D.50°
( http: / / www.21cnjy.com )
下列说法正确的是( )
A.与 ( http: / / www.21cnjy.com )圆有公共点的直线是圆的切线 B.到圆心距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线 D.过圆的半径外端的直线是圆的切线21世纪教育所有
如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是( )
( http: / / www.21cnjy.com )
A.30° B.45° C.50° D.60°
在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
2 、填空题(本大题共6小题 )
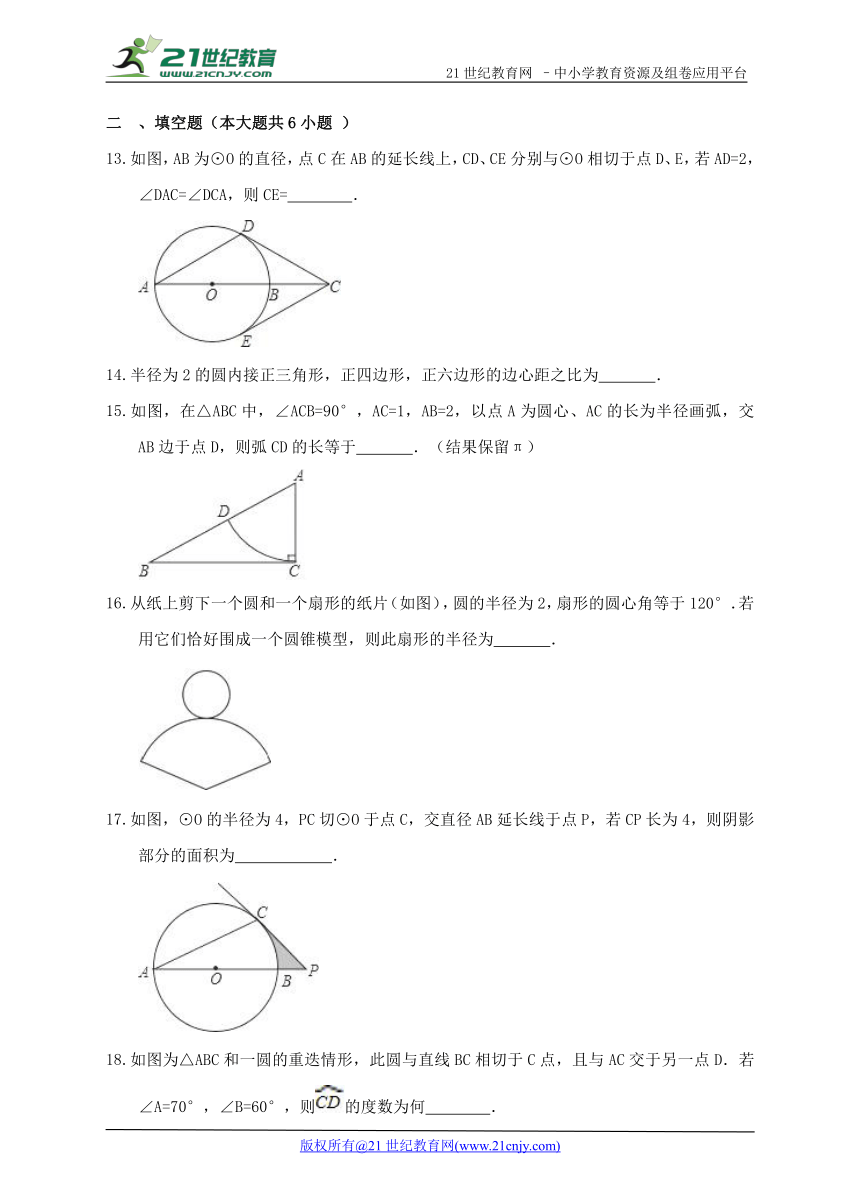
如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE= .
( http: / / www.21cnjy.com )www.21-cn-jy.com
半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为 .
如图,在△ABC中,∠ACB=90°,A ( http: / / www.21cnjy.com )C=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)2·1·c·n·j·y
( http: / / www.21cnjy.com )
从纸上剪下一个圆和一个扇形的纸片(如图) ( http: / / www.21cnjy.com ),圆的半径为2,扇形的圆心角等于120°.若用它们恰好围成一个圆锥模型,则此扇形的半径为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为 .21*cnjy*com
( http: / / www.21cnjy.com )
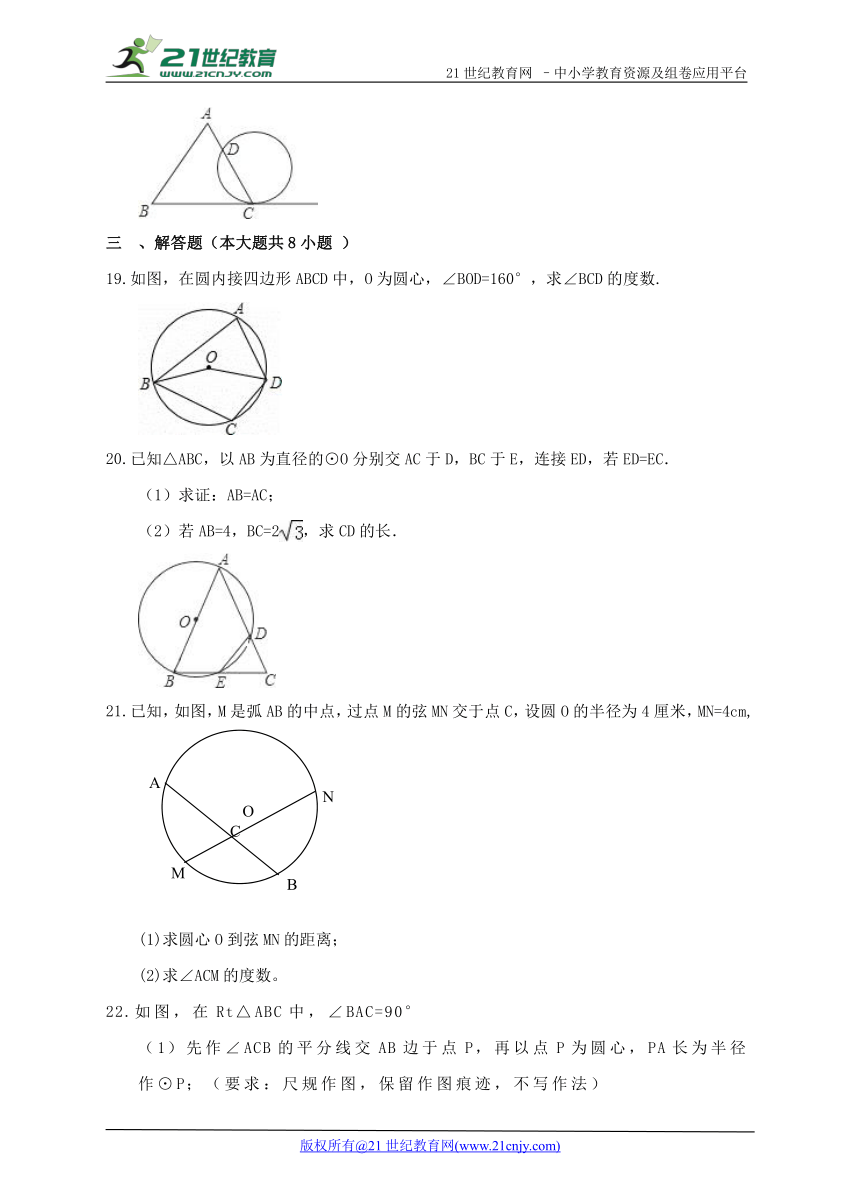
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则 ( http: / / www.21cnjy.com )的度数为何 .
( http: / / www.21cnjy.com )【来源:21cnj*y.co*m】
3 、解答题(本大题共8小题 )
如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2 ( http: / / www.21cnjy.com ),求CD的长.
( http: / / www.21cnjy.com )
已知,如图,M是弧AB的中点,过点M的弦MN交于点C,设圆O的半径为4厘米,MN=4cm,
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数。
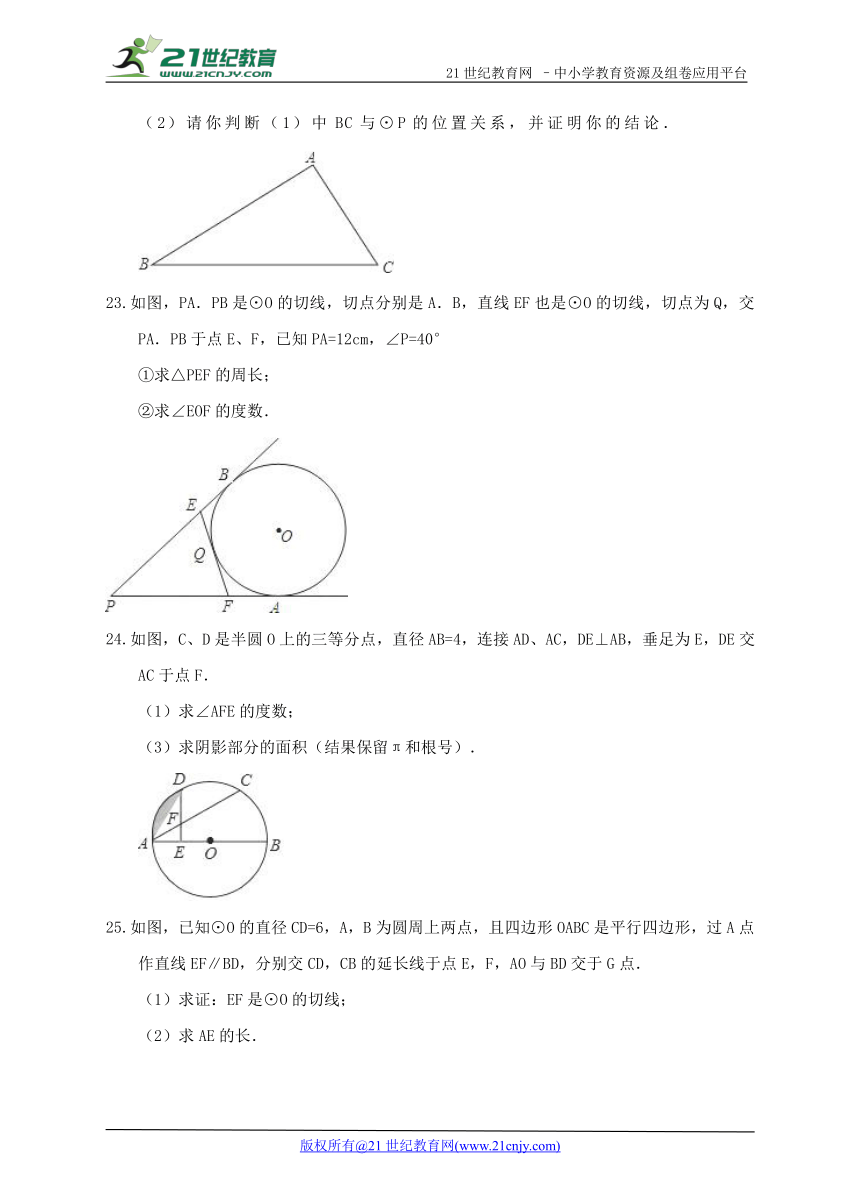
如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
( http: / / www.21cnjy.com )
如图,PA.PB是⊙O的 ( http: / / www.21cnjy.com )切线,切点分别是A.B,直线EF也是⊙O的切线,切点为Q,交PA.PB于点E、F,已知PA=12cm,∠P=40°
①求△PEF的周长;
②求∠EOF的度数.【出处:21教育名师】
( http: / / www.21cnjy.com )
如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.【版权所有:21教育】
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).
( http: / / www.21cnjy.com )
如图,已知⊙O的直径CD=6,A,B ( http: / / www.21cnjy.com )为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)求证:EF是⊙O的切线;
(2)求AE的长.
( http: / / www.21cnjy.com )
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.21*cnjy*com
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.
( http: / / www.21cnjy.com )
答案解析
1 、选择题。
1. 【分析】根据⊙O的半径为13,弦AB的长度是24,ON⊥AB,可以求得AN的长,从而可以求得ON的长.
解:由题意可得,
OA=13,∠ONA=90°,AB=24,
∴AN=12,
∴ON= ( http: / / www.21cnjy.com ),
故选A.
2. 【分析】由 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),可求得∠BOC=∠EOD=∠COD=34°,继而可求得∠AOE的度数;然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数.
解:如图,∵ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),∠COD=34°,
∴∠BOC=∠EOD=∠COD=34°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO= ( http: / / www.21cnjy.com )×(180°﹣78°)=51°.
故选:A.
3. 【分析】根据AB是⊙O的直径可得出∠ACB=90°,再根据三角形内角和为180°以及∠OBC=60°,即可求出∠BAC的度数.
解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠OBC=60°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=30°.
故选D.
4. 【分析】先求出∠ABC,根据圆内接四边形的对角互补求出即可.
解:∵∠EBA=125°,
∴∠ABC=180°﹣125°=55°,
∵四边形ABCD内接于⊙O,
∴∠D+∠ABC=180°,
∴∠D=180°﹣55°=125°,
故选C.
5. 【分析】利用等弧和弦的概念,垂径定理以及弧,弦与圆心角之间的关系进行判断.
解:A.弧的度数与所对圆心角的度数相等,所以同圆或等圆中弧相等,则它们所对的圆心角也相等,故本选项正确;
B、90°的圆周角所对的弦是直径,故本选项错误;
C、应强调这条弦不是直径,故本选项错误;
D、不在同一直线上的三点确定一个圆,故本选项错误.
故选:A.
6. 【分析】(1)点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外 d>r
②点P在圆上 d=r
①点P在圆内 d<r
(2)点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
解:∵点A为OP的中点,∴OA=OP÷2=5<6,
∴点A在☉O内部
故选C.
7. 【分析】利用圆周角定理以及圆内接四边形的性质得出∠BAC的度数.
解:如图所示:∵O是△ABC的外心 ( http: / / www.21cnjy.com ),∠BOC=80°,
∴∠A=40°,∠A′=140°,
故∠BAC的度数为:40°或140°.
故选:C.
8. 解:.由题意知圆的直径为12cm,那么圆的半径为6cm.则当直线与圆相交时,直线与圆心的距离d<6cm.
故选A
【分析】连接OA,根据切线的性质,即可求得∠C的度数.
9. 解:如图,连接OA,
( http: / / www.21cnjy.com )
∵AC是⊙O的切线,
∴∠OAC=90°,
∵OA=OB,
∴∠B=∠OAB=20°,
∴∠AOC=40°,
∴∠C=50°.
故选:D.
10. 【分析】根据切线的判定定理:经过半 ( http: / / www.21cnjy.com )径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.注意排除法在解选择题中的应用.
解:A.与圆只有一个交点的直线是圆的切线,故本选项错误;
B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;
C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;
D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.
故选B.
11. 【分析】根据弦切角的性质,得∠DAE=∠B, ( http: / / www.21cnjy.com )再由已知条件可得∠DAE=∠B=∠BAE,从而求出∠ABD.
解:∵AC是⊙O切线,
∴∠DAE=∠B,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠DAE=∠B=∠BAE,
∵BD⊥AC,
∴∠DAE=∠B=∠BAE=30°.
故选A.
12. 【分析】直角三角形的内切圆半径和其三边有特殊关系:三边中a b为直角边,c为斜边,内切圆半径为r,则r= ( http: / / www.21cnjy.com );外接圆的半径就是斜边的一半.
解:∵AB=5,AC=3,
∴BC= ( http: / / www.21cnjy.com )=4,
∴外接圆半径= ( http: / / www.21cnjy.com )=2.5,
∵四边形ODCE是正方形,且⊙O是△ABC的内切圆,
∴内切圆半径= ( http: / / www.21cnjy.com )=1.
故选C.
( http: / / www.21cnjy.com )
2 、填空题
13. 【分析】有条件可得AD=C ( http: / / www.21cnjy.com )D,再有切线长定理可得:CD=CE,所以AD=CE,问题的解.
解:∵CD、CE分别与⊙O相切于点D、E,
∴CD=CE,
∵∠DAC=∠DCA,
∴AD=CD,
∴AD=CE,
∵AD=2,
∴CE=2.
故答案为:2.
14. 【分析】根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.
解:由题意可得,
正三角形的边心距是:2×sin30°=2× ( http: / / www.21cnjy.com )=1,
正四边形的边心距是:2×sin45°=2× ( http: / / www.21cnjy.com ),
正六边形的边心距是:2×sin60°=2× ( http: / / www.21cnjy.com ),
∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ),
故答案为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ).
15. 【分析】先根据ACB=90°,AC=1,AB=2,得到∠ABC=30°,进而得出∠A=60°,再根据AC=1,即可得到弧CD的长.
解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,
又∵AC=1,
∴弧CD的长为 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
16. 【分析】圆的周长就是扇形的弧长,根据弧长的计算公式即可求得半径的长.
解:扇形的弧长是4π.
设圆的半径是r,则
( http: / / www.21cnjy.com )=4π,
解得:r=6.
故答案为:6.
17. 【分析】利用切线的性质结合等腰直角三角形的性质得出∠COP=∠CPO=45°,进而利用阴影部分的面积为:S△COP﹣S扇形COB求出即可.21·世纪*教育网
解:连接CO,
∵PC切⊙O于点C,
∴OC⊥PC,
∵⊙O的半径为4,CP长为4,
∴CO=CP,
∴∠COP=∠CPO=45°,
∴阴影部分的面积为:S△COP﹣S扇形COB= ( http: / / www.21cnjy.com )×4×4﹣ ( http: / / www.21cnjy.com )=8﹣2π.
故答案为:8﹣2π.
( http: / / www.21cnjy.com )
18. 【分析】根据三角形内角和定理求得∠ACB的度数,再根据弦切角等于它所夹的弧的度数的一半进行求解.
解:∵∠A=70°,∠B=60°,
∴∠ACB=50°,
又圆与直线BC相切于C点,
∴的度数=2∠ACB=50°×2=100°.
故答案为100°.2-1-c-n-j-y
3 、解答题
【分析】根据圆周角定理求出∠A的度数,根据圆内接四边形的性质得出∠A+∠BCD=180°,代入求出即可.21教育名师原创作品
解:∵∠BOD=160°
∴∠BAD=80°
∴∠BCD=180°-∠BAD=180°-80°=100°
19. 【分析】(1)由等腰三角 ( http: / / www.21cnjy.com )形的性质得到∠EDC=∠C,由圆外接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;
(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,由“三线合一”定理得到BE=CE= ( http: / / www.21cnjy.com )BC= ( http: / / www.21cnjy.com ),由割线定理可证得结论.
(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC;
(2)解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE= ( http: / / www.21cnjy.com )BC= ( http: / / www.21cnjy.com ),
∵CE CB=CD CA,AC=AB=4,
∴ ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com )=4CD,
∴CD= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
21. 【分析】(1)连接OM,由垂径定理可知 ( http: / / www.21cnjy.com )MD=ND,在Rt△MOD中,已知OM、MD,易求OD.
(2)利用锐角三角函数,易求∠OMD=30°,进而易求∠ACM=60°.
解:(1)连接OM. ∵点M是AB的中点,∴OM⊥AB.过点O作OD⊥MN于点D,
由垂径定理,得MD=1/2MN= ( http: / / www.21cnjy.com )∴在Rt△ODM中,OM=4,MD= ( http: / / www.21cnjy.com )
∴OD=2.故圆心O到弦MN的距离为2
(2)cos∠OMD=MD:OM = ( http: / / www.21cnjy.com ),∴∠OMD=30°,∴∠ACM= 60°
22. 【分析】(1)根据题意作出图形,如图所示;
(2)BC与⊙P相切,理由为:过P作PD⊥BC,交BC于点P,利用角平分线定理得到PD=PA,而PA为圆P的半径,即可得证.21教育网
解:(1)如图所示,⊙P为所求的圆;
(2)BC与⊙P相切,理由为:
过P作PD⊥BC,交BC于点P,
∵CP为∠ACB的平分线,且PA⊥AC,PD⊥CB,
∴PD=PA,
∵PA为⊙P的半径.
∴BC与⊙P相切.
( http: / / www.21cnjy.com )
23. 【分析】①根据切线长定理得出PA=PB,EB=EQ,FQ=FA,由PE+EF+PF=PE+EQ+FQ+PF即可求出答案.
②连接OE,OF,求出∠OEF+∠OFE的度数,即可得出∠EOF的度数.
解:①∵PA.PB是⊙O的切线,
∴PA=PB,
( http: / / www.21cnjy.com )21·cn·jy·com
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE= ( http: / / www.21cnjy.com )(∠P+∠PFE)+ ( http: / / www.21cnjy.com )∠(P+∠PEF)= ( http: / / www.21cnjy.com )(180°+40°)=110°,
∴∠EOF=180°-110°=70°.【来源:21·世纪·教育·网】
24. 【分析】(1)连接OD,OC,根据已知条件得到∠AOD=∠DOC=∠COB=60°,根据圆周角定理得到∠CAB=30°,于是得到结论;
(2)由(1)知,∠AOD=60°,推出△AOD是等边三角形,OA=2,得到DE= ( http: / / www.21cnjy.com ),根据扇形和三角形的面积公式即可得到结论.
解:(1)连接OD,OC,
∵C、D是半圆O上的三等分点,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠AOD=∠DOC=∠COB=60°,
∴∠CAB=30°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠AFE=90°﹣30°=60°;
(2)由(1)知,∠AOD=60°,
∵OA=OD,AB=4,
∴△AOD是等边三角形,OA=2,
∵DE⊥AO,
∴DE= ( http: / / www.21cnjy.com ),
∴S阴影=S扇形AOD﹣S△AOD= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
25. 【分析】(1)利用圆周角定理得到∠DB ( http: / / www.21cnjy.com )C=90°,再利用平行四边形的性质得AO∥BC,所以BD⊥OA,加上EF∥BD,所以OA⊥EF,于是根据切线的判定定理可得到EF是⊙O的切线;
(2)连接OB,如图,利用平行四边 ( http: / / www.21cnjy.com )形的性质得OA=BC,则OB=OC=BC,于是可判断△OBC为等边三角形,所以∠C=60°,易得∠AOE=∠C=60°,然后在Rt△OAE中利用正切的定义可求出AE的长.
(1)证明:∵CD为直径,
∴∠DBC=90°,
∴BD⊥BC,
∵四边形OABC是平行四边形,
∴AO∥BC,
∴BD⊥OA,
∵EF∥BD,
∴OA⊥EF,
∴EF是⊙O的切线;
(2)解:连接OB,如图,
∵四边形OABC是平行四边形,
∴OA=BC,
而OB=OC=OA,
∴OB=OC=BC,
∴△OBC为等边三角形,
∴∠C=60°,
∴∠AOE=∠C=60°,
在Rt△OAE中,∵tan∠AOE= ( http: / / www.21cnjy.com ),
∴AE=3tan60°=3 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
26. 【分析】(1)直线DE与圆O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;
(2)连接OE,设DE=x,则EB=ED ( http: / / www.21cnjy.com )=x,CE=8﹣x,在直角三角形OCE中,利用勾股定理列出关于x的方程,求出方程的得到x的值,即可确定出DE的长.
解:(1)直线DE与⊙O相切,理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠ODE=90°,
∴OC2+CE2=OE2=OD2+DE2,
∴42+(8﹣x)2=22+x2,
解得:x=4.75,
则DE=4.75.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
N
M
B
A
O
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
圆单元检测A卷
姓名:__________班级:__________考号:__________
1 、选择题(本大题共12小题 )
如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=( )
( http: / / www.21cnjy.com )
A.5 B.7 C.9 D.11
如图,AB是⊙O的直径, ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),∠COD=34°,则∠AEO的度数是( )
( http: / / www.21cnjy.com )
A.51° B.56° C.68° D.78°
如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
( http: / / www.21cnjy.com )
A.75° B.60° C.45° D.30°
如图,四边形ABCD内接于⊙O,E是CB的延长线上一点,∠EBA=125°,则∠D=( )
( http: / / www.21cnjy.com )
A.65° B.120° C.125° D.130°
下列说法正确的是( )
A.同圆或等圆中弧相等,则它们所对的圆心角也相等
B.90°的圆心角所对的弦是直径
C.平分弦的直径垂直于这条弦
D.三点确定一个圆
已知☉O的半径为6,A为线段PO的中点,当OP=10时,点A与☉O的位置关系为( )
A.在圆上 B.在圆外 C.在圆内 D.不确定
点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100° C.40°或140° D.40°或100°
圆最长弦为12cm,如果直线与圆相交,且直线与圆心的距离为d,那么( )
A.d<6cm B.6cm
如图,AB是⊙O的弦,AC是⊙Or切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )21cnjy.com
A.20° B.25° C. 40° D.50°
( http: / / www.21cnjy.com )
下列说法正确的是( )
A.与 ( http: / / www.21cnjy.com )圆有公共点的直线是圆的切线 B.到圆心距离等于圆的半径的直线是圆的切线
C.垂直于圆的半径的直线是圆的切线 D.过圆的半径外端的直线是圆的切线21世纪教育所有
如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是( )
( http: / / www.21cnjy.com )
A.30° B.45° C.50° D.60°
在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5
2 、填空题(本大题共6小题 )
如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,∠DAC=∠DCA,则CE= .
( http: / / www.21cnjy.com )www.21-cn-jy.com
半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为 .
如图,在△ABC中,∠ACB=90°,A ( http: / / www.21cnjy.com )C=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于 .(结果保留π)2·1·c·n·j·y
( http: / / www.21cnjy.com )
从纸上剪下一个圆和一个扇形的纸片(如图) ( http: / / www.21cnjy.com ),圆的半径为2,扇形的圆心角等于120°.若用它们恰好围成一个圆锥模型,则此扇形的半径为 .www-2-1-cnjy-com
( http: / / www.21cnjy.com )
如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为 .21*cnjy*com
( http: / / www.21cnjy.com )
如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则 ( http: / / www.21cnjy.com )的度数为何 .
( http: / / www.21cnjy.com )【来源:21cnj*y.co*m】
3 、解答题(本大题共8小题 )
如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2 ( http: / / www.21cnjy.com ),求CD的长.
( http: / / www.21cnjy.com )
已知,如图,M是弧AB的中点,过点M的弦MN交于点C,设圆O的半径为4厘米,MN=4cm,
(1)求圆心O到弦MN的距离;
(2)求∠ACM的度数。
如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
( http: / / www.21cnjy.com )
如图,PA.PB是⊙O的 ( http: / / www.21cnjy.com )切线,切点分别是A.B,直线EF也是⊙O的切线,切点为Q,交PA.PB于点E、F,已知PA=12cm,∠P=40°
①求△PEF的周长;
②求∠EOF的度数.【出处:21教育名师】
( http: / / www.21cnjy.com )
如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.【版权所有:21教育】
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).
( http: / / www.21cnjy.com )
如图,已知⊙O的直径CD=6,A,B ( http: / / www.21cnjy.com )为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)求证:EF是⊙O的切线;
(2)求AE的长.
( http: / / www.21cnjy.com )
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.21*cnjy*com
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.
( http: / / www.21cnjy.com )
答案解析
1 、选择题。
1. 【分析】根据⊙O的半径为13,弦AB的长度是24,ON⊥AB,可以求得AN的长,从而可以求得ON的长.
解:由题意可得,
OA=13,∠ONA=90°,AB=24,
∴AN=12,
∴ON= ( http: / / www.21cnjy.com ),
故选A.
2. 【分析】由 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),可求得∠BOC=∠EOD=∠COD=34°,继而可求得∠AOE的度数;然后再根据等腰三角形的性质和三角形内角和定理来求∠AEO的度数.
解:如图,∵ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),∠COD=34°,
∴∠BOC=∠EOD=∠COD=34°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO= ( http: / / www.21cnjy.com )×(180°﹣78°)=51°.
故选:A.
3. 【分析】根据AB是⊙O的直径可得出∠ACB=90°,再根据三角形内角和为180°以及∠OBC=60°,即可求出∠BAC的度数.
解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠OBC=60°,
∴∠BAC=180°﹣∠ACB﹣∠ABC=30°.
故选D.
4. 【分析】先求出∠ABC,根据圆内接四边形的对角互补求出即可.
解:∵∠EBA=125°,
∴∠ABC=180°﹣125°=55°,
∵四边形ABCD内接于⊙O,
∴∠D+∠ABC=180°,
∴∠D=180°﹣55°=125°,
故选C.
5. 【分析】利用等弧和弦的概念,垂径定理以及弧,弦与圆心角之间的关系进行判断.
解:A.弧的度数与所对圆心角的度数相等,所以同圆或等圆中弧相等,则它们所对的圆心角也相等,故本选项正确;
B、90°的圆周角所对的弦是直径,故本选项错误;
C、应强调这条弦不是直径,故本选项错误;
D、不在同一直线上的三点确定一个圆,故本选项错误.
故选:A.
6. 【分析】(1)点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外 d>r
②点P在圆上 d=r
①点P在圆内 d<r
(2)点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.
解:∵点A为OP的中点,∴OA=OP÷2=5<6,
∴点A在☉O内部
故选C.
7. 【分析】利用圆周角定理以及圆内接四边形的性质得出∠BAC的度数.
解:如图所示:∵O是△ABC的外心 ( http: / / www.21cnjy.com ),∠BOC=80°,
∴∠A=40°,∠A′=140°,
故∠BAC的度数为:40°或140°.
故选:C.
8. 解:.由题意知圆的直径为12cm,那么圆的半径为6cm.则当直线与圆相交时,直线与圆心的距离d<6cm.
故选A
【分析】连接OA,根据切线的性质,即可求得∠C的度数.
9. 解:如图,连接OA,
( http: / / www.21cnjy.com )
∵AC是⊙O的切线,
∴∠OAC=90°,
∵OA=OB,
∴∠B=∠OAB=20°,
∴∠AOC=40°,
∴∠C=50°.
故选:D.
10. 【分析】根据切线的判定定理:经过半 ( http: / / www.21cnjy.com )径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.注意排除法在解选择题中的应用.
解:A.与圆只有一个交点的直线是圆的切线,故本选项错误;
B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;
C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;
D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.
故选B.
11. 【分析】根据弦切角的性质,得∠DAE=∠B, ( http: / / www.21cnjy.com )再由已知条件可得∠DAE=∠B=∠BAE,从而求出∠ABD.
解:∵AC是⊙O切线,
∴∠DAE=∠B,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠DAE=∠B=∠BAE,
∵BD⊥AC,
∴∠DAE=∠B=∠BAE=30°.
故选A.
12. 【分析】直角三角形的内切圆半径和其三边有特殊关系:三边中a b为直角边,c为斜边,内切圆半径为r,则r= ( http: / / www.21cnjy.com );外接圆的半径就是斜边的一半.
解:∵AB=5,AC=3,
∴BC= ( http: / / www.21cnjy.com )=4,
∴外接圆半径= ( http: / / www.21cnjy.com )=2.5,
∵四边形ODCE是正方形,且⊙O是△ABC的内切圆,
∴内切圆半径= ( http: / / www.21cnjy.com )=1.
故选C.
( http: / / www.21cnjy.com )
2 、填空题
13. 【分析】有条件可得AD=C ( http: / / www.21cnjy.com )D,再有切线长定理可得:CD=CE,所以AD=CE,问题的解.
解:∵CD、CE分别与⊙O相切于点D、E,
∴CD=CE,
∵∠DAC=∠DCA,
∴AD=CD,
∴AD=CE,
∵AD=2,
∴CE=2.
故答案为:2.
14. 【分析】根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.
解:由题意可得,
正三角形的边心距是:2×sin30°=2× ( http: / / www.21cnjy.com )=1,
正四边形的边心距是:2×sin45°=2× ( http: / / www.21cnjy.com ),
正六边形的边心距是:2×sin60°=2× ( http: / / www.21cnjy.com ),
∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ),
故答案为:1: ( http: / / www.21cnjy.com ): ( http: / / www.21cnjy.com ).
15. 【分析】先根据ACB=90°,AC=1,AB=2,得到∠ABC=30°,进而得出∠A=60°,再根据AC=1,即可得到弧CD的长.
解:∵∠ACB=90°,AC=1,AB=2,
∴∠ABC=30°,
∴∠A=60°,
又∵AC=1,
∴弧CD的长为 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
故答案为: ( http: / / www.21cnjy.com ).
16. 【分析】圆的周长就是扇形的弧长,根据弧长的计算公式即可求得半径的长.
解:扇形的弧长是4π.
设圆的半径是r,则
( http: / / www.21cnjy.com )=4π,
解得:r=6.
故答案为:6.
17. 【分析】利用切线的性质结合等腰直角三角形的性质得出∠COP=∠CPO=45°,进而利用阴影部分的面积为:S△COP﹣S扇形COB求出即可.21·世纪*教育网
解:连接CO,
∵PC切⊙O于点C,
∴OC⊥PC,
∵⊙O的半径为4,CP长为4,
∴CO=CP,
∴∠COP=∠CPO=45°,
∴阴影部分的面积为:S△COP﹣S扇形COB= ( http: / / www.21cnjy.com )×4×4﹣ ( http: / / www.21cnjy.com )=8﹣2π.
故答案为:8﹣2π.
( http: / / www.21cnjy.com )
18. 【分析】根据三角形内角和定理求得∠ACB的度数,再根据弦切角等于它所夹的弧的度数的一半进行求解.
解:∵∠A=70°,∠B=60°,
∴∠ACB=50°,
又圆与直线BC相切于C点,
∴的度数=2∠ACB=50°×2=100°.
故答案为100°.2-1-c-n-j-y
3 、解答题
【分析】根据圆周角定理求出∠A的度数,根据圆内接四边形的性质得出∠A+∠BCD=180°,代入求出即可.21教育名师原创作品
解:∵∠BOD=160°
∴∠BAD=80°
∴∠BCD=180°-∠BAD=180°-80°=100°
19. 【分析】(1)由等腰三角 ( http: / / www.21cnjy.com )形的性质得到∠EDC=∠C,由圆外接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;
(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,由“三线合一”定理得到BE=CE= ( http: / / www.21cnjy.com )BC= ( http: / / www.21cnjy.com ),由割线定理可证得结论.
(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC;
(2)解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE= ( http: / / www.21cnjy.com )BC= ( http: / / www.21cnjy.com ),
∵CE CB=CD CA,AC=AB=4,
∴ ( http: / / www.21cnjy.com ) 2 ( http: / / www.21cnjy.com )=4CD,
∴CD= ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
21. 【分析】(1)连接OM,由垂径定理可知 ( http: / / www.21cnjy.com )MD=ND,在Rt△MOD中,已知OM、MD,易求OD.
(2)利用锐角三角函数,易求∠OMD=30°,进而易求∠ACM=60°.
解:(1)连接OM. ∵点M是AB的中点,∴OM⊥AB.过点O作OD⊥MN于点D,
由垂径定理,得MD=1/2MN= ( http: / / www.21cnjy.com )∴在Rt△ODM中,OM=4,MD= ( http: / / www.21cnjy.com )
∴OD=2.故圆心O到弦MN的距离为2
(2)cos∠OMD=MD:OM = ( http: / / www.21cnjy.com ),∴∠OMD=30°,∴∠ACM= 60°
22. 【分析】(1)根据题意作出图形,如图所示;
(2)BC与⊙P相切,理由为:过P作PD⊥BC,交BC于点P,利用角平分线定理得到PD=PA,而PA为圆P的半径,即可得证.21教育网
解:(1)如图所示,⊙P为所求的圆;
(2)BC与⊙P相切,理由为:
过P作PD⊥BC,交BC于点P,
∵CP为∠ACB的平分线,且PA⊥AC,PD⊥CB,
∴PD=PA,
∵PA为⊙P的半径.
∴BC与⊙P相切.
( http: / / www.21cnjy.com )
23. 【分析】①根据切线长定理得出PA=PB,EB=EQ,FQ=FA,由PE+EF+PF=PE+EQ+FQ+PF即可求出答案.
②连接OE,OF,求出∠OEF+∠OFE的度数,即可得出∠EOF的度数.
解:①∵PA.PB是⊙O的切线,
∴PA=PB,
( http: / / www.21cnjy.com )21·cn·jy·com
又∵直线EF是⊙O的切线,
∴EB=EQ,FQ=FA,
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm;
②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,
则∠OEF+∠OFE= ( http: / / www.21cnjy.com )(∠P+∠PFE)+ ( http: / / www.21cnjy.com )∠(P+∠PEF)= ( http: / / www.21cnjy.com )(180°+40°)=110°,
∴∠EOF=180°-110°=70°.【来源:21·世纪·教育·网】
24. 【分析】(1)连接OD,OC,根据已知条件得到∠AOD=∠DOC=∠COB=60°,根据圆周角定理得到∠CAB=30°,于是得到结论;
(2)由(1)知,∠AOD=60°,推出△AOD是等边三角形,OA=2,得到DE= ( http: / / www.21cnjy.com ),根据扇形和三角形的面积公式即可得到结论.
解:(1)连接OD,OC,
∵C、D是半圆O上的三等分点,
∴ ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),
∴∠AOD=∠DOC=∠COB=60°,
∴∠CAB=30°,
∵DE⊥AB,
∴∠AEF=90°,
∴∠AFE=90°﹣30°=60°;
(2)由(1)知,∠AOD=60°,
∵OA=OD,AB=4,
∴△AOD是等边三角形,OA=2,
∵DE⊥AO,
∴DE= ( http: / / www.21cnjy.com ),
∴S阴影=S扇形AOD﹣S△AOD= ( http: / / www.21cnjy.com )﹣ ( http: / / www.21cnjy.com )×2 ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com )π﹣ ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
25. 【分析】(1)利用圆周角定理得到∠DB ( http: / / www.21cnjy.com )C=90°,再利用平行四边形的性质得AO∥BC,所以BD⊥OA,加上EF∥BD,所以OA⊥EF,于是根据切线的判定定理可得到EF是⊙O的切线;
(2)连接OB,如图,利用平行四边 ( http: / / www.21cnjy.com )形的性质得OA=BC,则OB=OC=BC,于是可判断△OBC为等边三角形,所以∠C=60°,易得∠AOE=∠C=60°,然后在Rt△OAE中利用正切的定义可求出AE的长.
(1)证明:∵CD为直径,
∴∠DBC=90°,
∴BD⊥BC,
∵四边形OABC是平行四边形,
∴AO∥BC,
∴BD⊥OA,
∵EF∥BD,
∴OA⊥EF,
∴EF是⊙O的切线;
(2)解:连接OB,如图,
∵四边形OABC是平行四边形,
∴OA=BC,
而OB=OC=OA,
∴OB=OC=BC,
∴△OBC为等边三角形,
∴∠C=60°,
∴∠AOE=∠C=60°,
在Rt△OAE中,∵tan∠AOE= ( http: / / www.21cnjy.com ),
∴AE=3tan60°=3 ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
26. 【分析】(1)直线DE与圆O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;
(2)连接OE,设DE=x,则EB=ED ( http: / / www.21cnjy.com )=x,CE=8﹣x,在直角三角形OCE中,利用勾股定理列出关于x的方程,求出方程的得到x的值,即可确定出DE的长.
解:(1)直线DE与⊙O相切,理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
∴直线DE与⊙O相切;
(2)连接OE,
设DE=x,则EB=ED=x,CE=8﹣x,
∵∠C=∠ODE=90°,
∴OC2+CE2=OE2=OD2+DE2,
∴42+(8﹣x)2=22+x2,
解得:x=4.75,
则DE=4.75.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
N
M
B
A
O
C
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
