第1章 二次函数单元检测B卷
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
二次函数单元检测B卷
姓名:__________班级:__________考号:__________
1 、选择题(本大题共12小题 )
已知二次函数y=a(x﹣1)2+3,当x<1时,y随x的增大而增大,则a取值范围是( )
A.a≥0 B.a≤0 C.a>0 D.a<0
下列哪一个是假命题( )
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2 C.x<﹣2或x>1 D.﹣2<x<1
抛物线y=(x+2)2+3的顶点坐标是( )
A.(﹣2,3) B.(2,3) C.(﹣2,﹣3) D.(2,﹣3)
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
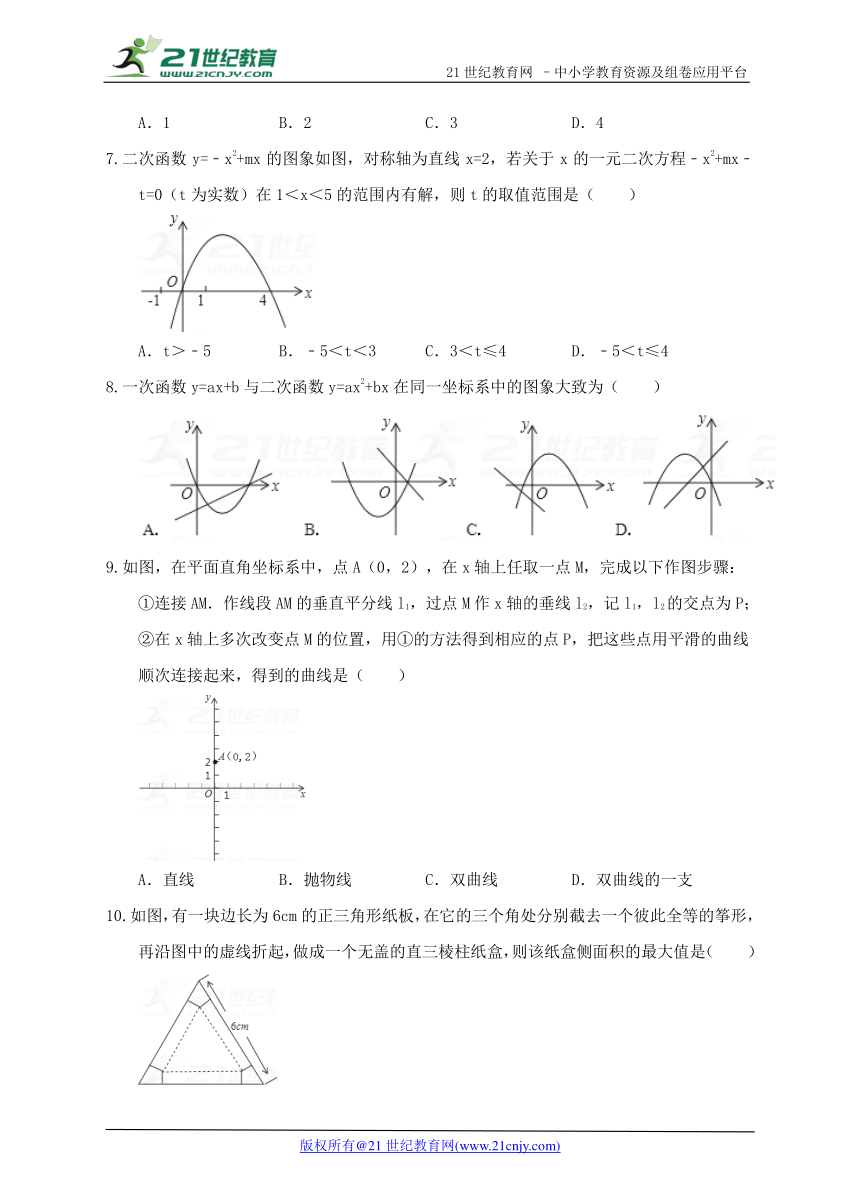
二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5 B.﹣5<t<3 C.3<t≤4 D.﹣5<t≤4
一次函数y=ax+b与二次函数y=ax2+bx在同一坐标系中的图象大致为( )
如图,在平面直角坐标系中,点A(0,2),在x轴上任取一点M,完成以下作图步骤:
①连接AM.作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1,l2的交点为P;
②在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线顺次连接起来,得到的曲线是( )21世纪教育网版权所有
A.直线 B.抛物线 C.双曲线 D.双曲线的一支
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.cm2 B.cm2 C.cm2 D.cm2
如图,在平面直角坐标系中,抛物线y=经过平移得到抛物线y=,其对称轴与两段抛物线所围成的阴影部分的面积为( )21教育网
A.2 B.4 C.8 D.16
规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);21·cn·jy·com
④若点(m,n)在反比例函数y=的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A.①② B.③④ C.②③ D.②④
2 、填空题(本大题共6小题 )
二次函数y=ax2+bx+c的图象上部分点的对应值如下表:
x ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3
y 6 0 ﹣4 ﹣6 ﹣6 ﹣4 0 6
则使y<0的x的取值范围是__________.
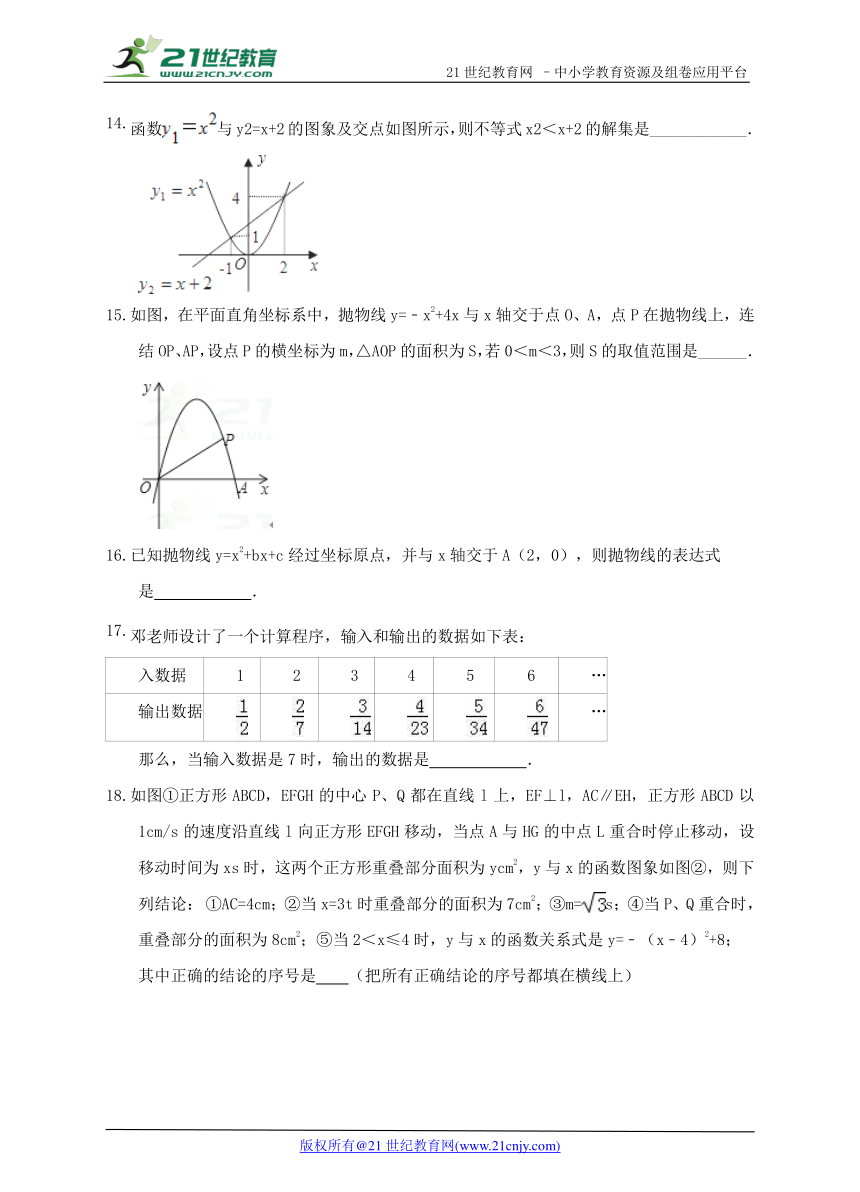
函数与y2=x+2的图象及交点如图所示,则不等式x2<x+2的解集是____________.
【来源:21·世纪·教育·网】
如图,在平面直角坐标系中,抛物线y=﹣x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是______.
已知抛物线y=x2+bx+c经过坐标原点,并与x轴交于A(2,0),则抛物线的表达式是 .2-1-c-n-j-y
邓老师设计了一个计算程序,输入和输出的数据如下表:
入数据 1 2 3 4 5 6 …
输出数据 …
那么,当输入数据是7时,输出的数据是 .
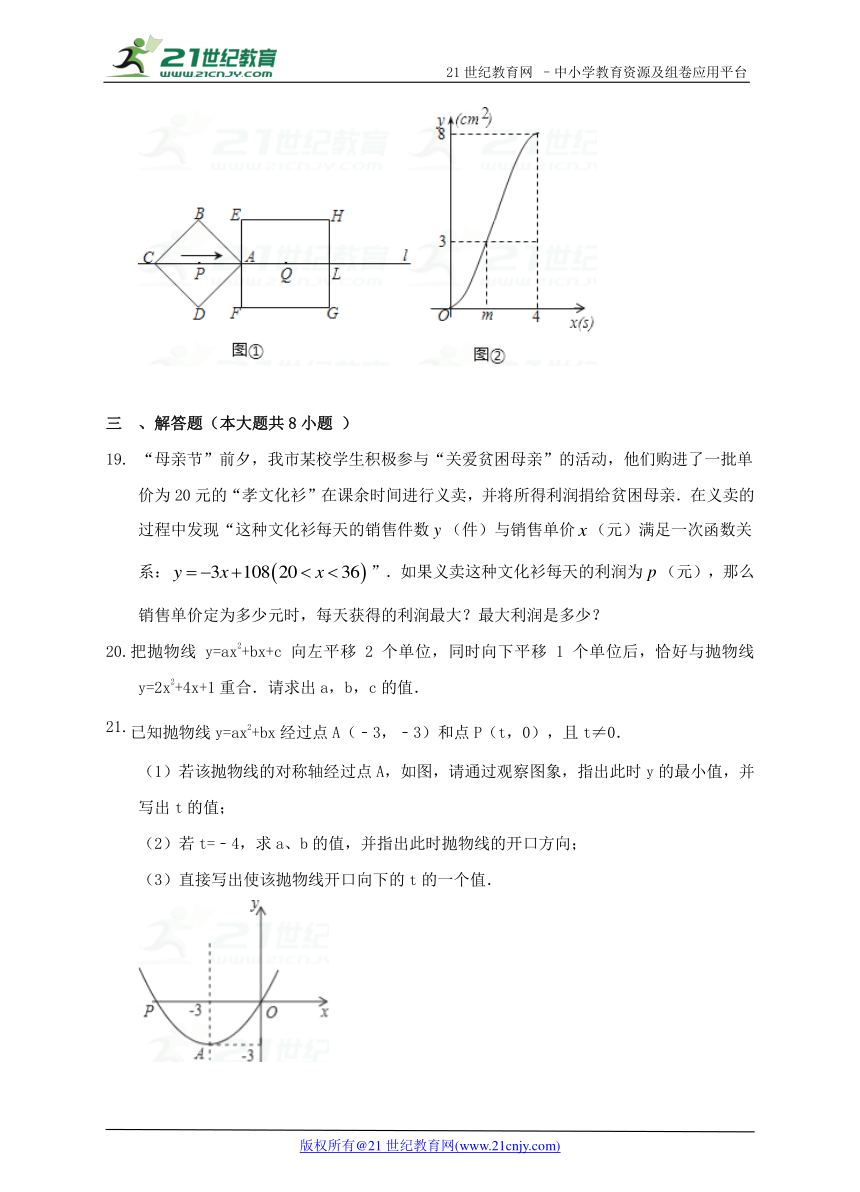
如图①正方形ABCD,EFGH的中心P、Q都在直线l上,EF⊥l,AC∥EH,正方形ABCD以1cm/s的速度沿直线l向正方形EFGH移动,当点A与HG的中点L重合时停止移动,设移动时间为xs时,这两个正方形重叠部分面积为ycm2,y与x的函数图象如图②,则下列结论:2①AC=4cm;②当x=3t时重叠部分的面积为7cm2;③m=s;④当P、Q重合时,重叠部分的面积为8cm2;⑤当2<x≤4时,y与x的函数关系式是y=﹣(x﹣4)2+8;
其中正确的结论的序号是 (把所有正确结论的序号都填在横线上)
3 、解答题(本大题共8小题 )
“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进了一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.在义卖的过程中发现“这种文化衫每天的销售件数(件)与销售单价(元)满足一次函数关系:”.如果义卖这种文化衫每天的利润为(元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少?
把抛物线y=ax2+bx+c向左平移2个单位,同时向下平移1个单位后,恰好与抛物线y=2x2+4x+1重合.请求出a,b,c的值.2·1·c·n·j·y
已知抛物线y=ax2+bx经过点A(﹣3,﹣3)和点P(t,0),且t≠0.
(1)若该抛物线的对称轴经过点A,如图,请通过观察图象,指出此时y的最小值,并写出t的值;
(2)若t=﹣4,求a、b的值,并指出此时抛物线的开口方向;
(3)直接写出使该抛物线开口向下的t的一个值.
把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).【版权所有:21教育】
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.21教育名师原创作品
一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x
(1)求x=2时,平行四边形AGEF的面积.
(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?
如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣x2+bx+c经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
如图1,在平面直角坐标系中,二次函数y=x2+bx的图象与x轴交于点A(6,0),△OBC的B点坐标(3,4),C点坐标为(5,0).
(1)求二次函数的关系式;
(2)将△OBC沿边BC翻折,点O落在点D,请求出点D的坐标并判断点D是否在二次函数的图象上;
(3)在(2)的条件下,如图2,点E的坐标为(0,8),有一动点P从E点出发沿EO方向以2个单位/s的速度向下运动,过点P的直线l平行于x轴,当点P运动到点O时停止运动,设运动时间为t(s),其中0≤t≤4.请探究直线l上是否存在点H,使得△ODH为直角三角形?若存在,请直接写出满足条件的点H的个数及相应t的取值范围,不需说明理由;若不存在,请说明理由.
如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0)
(1)求该抛物线的解析式.
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
答案解析
1 、选择题
1. 【分析】根据二次函数y=a(x﹣1)2+3,当x<1时,y随x的增大而增大,可以得到该二次函数的对称轴,和相应的a的值,从而可以解答本题.
解:∵二次函数y=a(x﹣1)2+3,
∴该二次函数的对称轴为直线x=1,
又∵当x<1时,y随x的增大而增大,
∴a<0,
故选D.
2. 【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解:A.五边形外角和为360°是真命题,故A不符合题意;
B、切线垂直于经过切点的半径是真命题,故B不符合题意;
C、(3,﹣2)关于y轴的对称点为(﹣3,2)是假命题,故C符合题意;
D、抛物线y=x2﹣4x+2017对称轴为直线x=2是真命题,故D不符合题意;
故选:C.
3. 【分析】先求出函数的图象与x轴的交点坐标,再根据函数的图象开口向下,即可得出当y<0时自变量x的取值范围.21·世纪*教育网
解:当y=0时,﹣x2+x+2=0,
(x+1)(﹣x+2)=0,
x1=﹣1,x2=2,
由于函数开口向下,
可知当y<0时,自变量x的取值范围是x<﹣1或x>2.
故选A
4. 【分析】抛物线y=a(x﹣h)2+k,顶点坐标是(h,k),直接根据抛物线y=(x+2)2+3写出顶点坐标则可.
解:由于y=(x+2)2+3为抛物线的顶点式,根据顶点式的坐标特点可知,抛物线的顶点坐标为(﹣2,3).
故选:A.
5. 解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4c<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确.
故选B.
6. 【分析】利用抛物线的性质解决
解:根据函数图象可知: 抛物线开口向上,所以a>o 对称抽为x-1 所以b>0,物线与y轴交于正半轴,所以c+2>2 ,c>o 所以abc>o 故①错误,
因为抛物线与x抽只有一个交点,所以b2-4a(c+2)=0,所以②错误,
因为对称抽为x=-1 所以-=-1,所以b=2a,把点(- 1,0)代入解析式得: a-b+c+2=0 ,所以a-2a+c+2=0 ,所以a=c+2 >2 所以③正确,
根据抛物线的对称性可得:当x=-2时, y=4a-2b+c+2 >2 所以4a-2b+c>0所以④正确,
因此共有③④正确,
故选B
7. 【分析】如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.
解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故答案为D.
8. 【分析】对于每个选项,先根据二次函数的图象确定a和b的符号,然后根据一次函数的性质看一次函数图象的位置是否正确,若正确,说明它们可在同一坐标系内存在.
解:A.由二次函数y=ax2+bx的图象得a>0,b<0,则一次函数y=ax+b经过第一、三、四象限,且它们的交点为(1,0),所以A选项正确;
B、由二次函数y=ax2+bx的图象得a>0,b>0,则一次函数y=ax+b经过第一、二、三象限,所以B选项错误;
C、由二次函数y=ax2+bx的图象得a<0,b>0,则一次函数y=ax+b经过第一、二、四象限,所以C选项错误;
D、由二次函数y=ax2+bx的图象得a<0,b<0,则一次函数y=ax+b经过第二、三、四象限,所以D选项错误.
故选A.
9. 【分析】按照给定的作图步骤作图,根据图形中曲线的特征即可得出该曲线为抛物线.
解:根据作图步骤作图,如图所示.
由此即可得出该曲线为抛物线.
故选B/
10. 【分析】如图,由等边三角形的性质可以得出∠A=∠B=∠C=60°,由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK,根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO为矩形,且全等.连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°,设OD=x,则AO=2x,由勾股定理就可以求出AD=x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=x,
∴DE=6﹣2x,
∴纸盒侧面积=3x(6﹣2x)=﹣6x2+18x,
=﹣6(x﹣)2+,
∴当x=时,纸盒侧面积最大为.
故选C.
.
11. 解:过点C作CA⊥y,
∵抛物线y==(x2﹣4x)=(x2﹣4x+4)﹣2=(x﹣2)2﹣2,
∴顶点坐标为C(2,﹣2),
对称轴与两段抛物线所围成的阴影部分的面积为:2×2=4,
故选:B.
12. 【分析】①通过解方程得到该方程的根,结合“倍根方程”的定义进行判断;
②设x2=2x1,得到x1 x2=2x12=2,得到当x1=1时,x2=2,当x1=﹣1时,x2=﹣2,于是得到结论;【来源:21cnj*y.co*m】
③根据“倍根方程”的定义即可得到结论;
④若点(m,n)在反比例函数y=的图象上,得到mn=4,然后解方程mx2+5x+n=0即可得到正确的结论;【出处:21教育名师】
解:①由x2﹣2x﹣8=0,得
(x﹣4)(x+2)=0,
解得x1=4,x2=﹣2,
∵x1≠2x2,或x2≠2x1,
∴方程x2﹣2x﹣8=0不是倍根方程.
故①错误;
②关于x的方程x2+ax+2=0是倍根方程,
∴设x2=2x1,
∴x1 x2=2x12=2,
∴x1=±1,
当x1=1时,x2=2,
当x1=﹣1时,x2=﹣2,
∴x1+x2=﹣a=±3,
∴a=±3,故②正确;
③关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,
∴x2=2x1,
∵抛物线y=ax2﹣6ax+c的对称轴是直线x=3,
∴抛物线y=ax2﹣6ax+c与x轴的交点的坐标是(2,0)和(4,0),
故③正确;
④∵点(m,n)在反比例函数y=的图象上,
∴mn=4,
解mx2+5x+n=0得x1=﹣,x2=﹣,
∴x2=4x1,
∴关于x的方程mx2+5x+n=0不是倍根方程;
故选C.
2 、填空题
13.【分析】 根据图表信息判断出二次函数图象开口向下,然后写出函数值小于0的x的取值范围即可.21*cnjy*com
解:由表可知,抛物线开口向下,
∵x=﹣3,x=2时,y=0,
∴使y<0的x的取值范围是﹣3<x<2.
故答案为:﹣3<x<2.
14.【分析】利用函数图象得出交点坐标,利用一次函数图象只有在二次函数图象上方时,不等式x2<x+2,进而得出答案.
【解析】
利用图象得出函数与y2=x+2的图象交点坐标分别为:(-1,1)和(2,4),
∴不等式x2<x+2的解集为:-1<x<2.
故答案为:-1<x<2.
15.【分析】表示出P点坐标,进而表示出△PAB的底与高的长度,即可得出S与m的关系式,利用配方法可得△PAB的面积S的取值范围.
解:由题意,P点坐标为:(m,﹣m2+4m),
∵抛物线y=﹣x2+4x与x轴交于点O、A,
∴当y=0时,﹣x2+4x=0,
解得:x=0,或x=4,
∴A(4,0),
∴OA=4,
由题意可得:P到AB的距离为﹣m2+4m,
∴S=×4×(﹣m2+4m)=﹣2m2+8m=﹣2(m﹣2)2+8;
∵0<m<3,
∴0<S≤8.
故答案为:0<S≤8.
16.【分析】 把(0,0)代入可得出c的值,再把A(2,0)代入y=x2+bx得b的值,即可得出抛物线的表达式.
解:∵抛物线y=x2+bx+c经过坐标原点,
∴c=0,
把A(2,0)代入y=x2+bx得b=﹣2.
∴抛物线的表达式为y=x2﹣2x.
故答案为:y=x2﹣2x.
17.【分析】此题中分子的规律很好找,就是1,2,3,4,5,6…即第7次是7,但分母的规律就不好找了,这时我们可以列一个二次函数代入求.
解:从图中可以看出,分子上输入数据是n,分子就是n.
分母上我们可以列一个二次函数,可设分母为y,输入数据为x,则y=ax2+bx+c,把x=1,2,3代入代数式得:解得:
把这代入方程得:y=x2+2x﹣1,
所以当输出数据是7时,分母=49+14﹣1=62,
所以输出的数据是.
故答案为.
18.【分析】 ①由这两个正方形的重叠部分面积为8时,也就是小正方形的面积为8,求出边长即可得出AC的长;www-2-1-cnjy-com
②当2≤x≤6时,得到y与x的函数关系式,当y=7时,解方程可作判断;
③当6≤x≤8时,y与x的函数关系式为y=(8﹣x)2,此时函数y的取值范围是0≤y≤4.当y=3时,解方程即可求出m;
④由图象可得结论;
⑤当2≤x≤6时,y与x的函数关系式为y=﹣(x﹣4)2+8.
解:(1)当这两个正方形的重叠部分面积为8时,也就是小正方形的面积为8,得出小正方形的边长为2cm,所以AC=×2=4cm,故①正确.
(2)当2≤x≤6时,y与x的函数关系式为y=﹣(x﹣4)2+8,此时函数y的取值范围是4≤y≤8,当y=7时,得﹣(x﹣4)2+8=7,解得x=3或x=5.所以正方形ABCD出发3秒或5秒时,重叠部分面积为7cm2,故②正确;
(3)当0≤x≤2时,y与x的函数关系式为y=x2,此时函数y的取值范围是0≤y≤4,当y=3时,得x2=3或(8﹣x)2=3,解得x=±(负号舍去)或x=±+8(正号舍去),即m=,故③正确;
(4)由图象可以看出两个正方形的最大重叠部分面积为8,此时P、Q重合,故④正确;
(5)当2≤x≤6时,y与x的函数关系式为y=﹣(x﹣4)2+8,故⑤正确;
故答案为:①②③④⑤.
3 、解答题
19.解:每天获得的利润为:
∵
∴当销售价定为28元时,每天获得的利润最大,
最大利润是192元.
20.【分析】根据目标函数图象向相反的方向平移,可得原函数图象,根据图象右移减,上移加,可得答案.
解:将y=2x2+4x+1
整理得y=2x2+4x+1=2(x+1)2﹣1.
因为抛物线y=ax2+bx+c 向左平移2个单位,再向下平移1个单位得y=2x2+4x+1=2(x+1)2﹣1,
所以将y=2x2+4x+1=2(x+1)2﹣1向右平移2个单位,再向上平移1个单位即得y=ax2+bx+c,
故y=ax2+bx+c=2(x+1﹣2)﹣1+1=2(x﹣1)=2x2﹣4x+2,
所以a=2,b=﹣4,c=2.
21.【分析】(1)由图可以看出A点为抛物线的顶点,且开口向上,所以此点即为此函数的最小值;
(2)点p是抛物线与x轴的一个交点,而此时另一个交点是0,那么P与O是关于抛物线对称轴的两个对称点,知道了对称点的坐标,就很容易求出t的值;
(3)a>0时,抛物线的开口向上,a<0时,抛物线的开口向下,求出a的值就知道其开口方向.
解:(1)∵抛物线的对称轴经过点A,
∴A点为抛物线的顶点,
∴y的最小值为﹣3,
∵P点和O点对称,
∴t=﹣6;
(2)分别将(﹣4,0)和(﹣3,﹣3)代入y=ax2+bx,得:,
解得,
∴抛物线开口方向向上;
(3)将A(﹣3,﹣3)和点P(t,0)代入y=ax2+bx,
,
由①得,b=3a+1③,
把③代入②,得at2+t(3a+1)=0,
∵t≠0,∴at+3a+1=0,
∴a=﹣.
∵抛物线开口向下,∴a<0,
∴﹣<0,
∴t+3>0,
∴t>﹣3.
故t的值可以是﹣1(答案不唯一).
(注:写出t>﹣3且t≠0或其中任意一个数均给分)
22.【分析】(1)将t=3代入解析式可得;
(2)根据h=10可得关于t的一元二次方程,解方程即可;
(3)由题意可得方程20t﹣t2=m 的两个不相等的实数根,由根的判别式即可得m的范围.
解:(1)当t=3时,h=20t﹣5t2=20×3﹣5×9=15(米),
∴当t=3时,足球距离地面的高度为15米;
(2)∵h=10,
∴20t﹣5t2=10,即t2﹣4t+2=0,
解得:t=2+或t=2﹣,
故经过2+或2﹣时,足球距离地面的高度为10米;
(3)∵m≥0,由题意得t1,t2是方程20t﹣5t2=m 的两个不相等的实数根,
∴b2﹣4ac=202﹣20m>0,
∴m<20,
故m的取值范围是0≤m<20.
23.【分析】设平行四边形AGEF的面积是S.利用平行四边形AGEF的对边互相平行知EF∥AG,所以同位角∠A=∠CFE=30°;然后在直角三角形ABC和直角三角形BEF中利用锐角三角函数的定义求得CF、AC的长度,从而求得平行四边形AGEF的底边AF=AC﹣CF;最后根据平行四边形的面积公式S=底×高得出关于S与x的函数关系式S=﹣x2+6x;21cnjy.com
(1)将x=2代入S与x的函数关系式S=﹣x2+6x,并求解即可;
(2)利用配方法求二次函数的最值.
解:设平行四边形AGEF的面积是S.
∵四边形AGEF是平行四边形,
∴EF∥AG;
∵∠A=30°,∠C=90°,CE=x,BC=6,
∴∠A=∠CFE=30°,
∴CF=x,AC=6,
∴AF=6﹣x;
∴S=AF CE=(6﹣x)x=﹣x2+6x,即S=﹣x2+6x;
(1)当x=2时,S=﹣4+12=8,即S=8.
答:平行四边形AGEF的面积为(平方单位)
(2)由S=﹣x2+6x,得
,
∴,
∴当x=3时,平行四边形AGEF的面积最大,最大面积是(平方单位)
24.【分析】(1)由旋转性质可得CD=AB=1、OA=OC=2,从而得出点B、D坐标,代入解析式即可得出答案;
(2)由直线OP把△BOD的周长分成相等的两部分且OB=OD,知DQ=BQ,即点Q为BD的中点,从而得出点Q坐标,求得直线OP解析式,代入抛物线解析式可得点P坐标.
解:(1)∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1、OA=OC=2,
则点B(2,1)、D(﹣1,2),代入解析式,得:
,
解得:,
∴二次函数的解析式为y=﹣x2+x+;
(2)如图,
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,
∴DQ=BQ,即点Q为BD的中点,
∴点Q坐标为(,),
设直线OP解析式为y=kx,
将点Q坐标代入,得: k=,
解得:k=3,
∴直线OP的解析式为y=3x,
代入y=﹣x2+x+,得:﹣ x2+x+=3x,
解得:x=1或x=﹣4(舍),
当x=1时,y=3,
∴点P坐标为(1,3).
25.【分析】(1)把A点坐标代入y=x2+bx,求出b的值,即可求出二次函数的关系式.
(2)首先由B、C坐标证得OB=OC,再根据翻折的性质可证得四边形OBDC为菱形,进而判断出四边形BMND是矩形,所以MN=BD=5,DN=BM=4,ON=OM+MN=3+5=8,据此求出点D的坐标,然后把点D的坐标代入抛物线解析式,即可判断出点D是否在二次函数的图象上.www.21-cn-jy.com
(3)首先求出当l和BD重合时,l和x轴重合时,t的值各是多少;然后分类讨论:①当0≤t<3﹣,t=2或t=4时;②当t=3﹣时;③当3﹣<t<2,或2<t<4时;根据△ODH为直角三角形,写出所有满足条件的点H的个数及相应t的取值范围即可.
解:(1)将点A(6,0)代入y=x2+bx,可得
0=+6b,
解得b=﹣,
∴二次函数的关系式是y=x2﹣x.
(2)如图1,过点B作BM⊥x轴于点M,过点D作DN⊥x轴于点N,
,
将△OBC沿边BC翻折,点O落在点D,
∵△OBC的B点坐标(3,4),C点坐标为(5,0),
∴OM=3,BM=4,OC=5,
∴OB=,
∴OB=OC,
∵将△OBC沿边BC翻折得到△DBC,
∴△OBC≌△DBC,
∴OB=DB,OC=DC,
又∵OB=OC,
∴OB=DB=OC=DC,
∴四边形OBDC是菱形,
∴BD∥x轴,
∵BM⊥x轴,DN⊥x轴,
∴BM∥DN,
∴四边形BMND是平行四边形,
∵∠BMN=90°,
∴四边形BMND是矩形,
∴MN=BD=5,DN=BM=4,
∴ON=OM+MN=3+5=8,
∴点D的坐标是(8,4),
∵当x=8时,y=×82﹣×8=4,
∴点D是否在二次函数的图象上.
(3)由(2)可得四边形OBDC是菱形,
∴BD∥x轴,
当l和BD重合时,
∵8﹣2t=4,
∴t=2,点H的个数是2个;
当l和x轴重合时,
∵8﹣2t=0,
∴t=4,点H的个数是2个;
①当0≤t<3﹣,t=2或t=4时,
点H的个数是2个.
②当t=3﹣时,
点H的个数是3个.
③当3﹣<t<2,或2<t<4时,
点H的个数是4个.
26.解:(1)把点C(0,﹣4),B(2,0)分别代入y=x2+bx+c中,
得,
解得
∴该抛物线的解析式为y=x2+x﹣4.
(2)令y=0,即x2+x﹣4=0,解得x1=﹣4,x2=2,
∴A(﹣4,0),S△ABC=AB OC=12.
设P点坐标为(x,0),则PB=2﹣x.
∵PE∥AC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△PBE∽△ABC,
∴,即,
化简得:S△PBE=(2﹣x)2.
S△PCE=S△PCB﹣S△PBE=PB OC﹣S△PBE=×(2﹣x)×4﹣(2﹣x)2
=x2﹣x+
=(x+1)2+3
∴当x=﹣1时,S△PCE的最大值为3.
(3)△OMD为等腰三角形,可能有三种情形:(I)当DM=DO时,如答图①所示.
DO=DM=DA=2,
∴∠OAC=∠AMD=45°,
∴∠ADM=90°,
∴M点的坐标为(﹣2,﹣2);
(II)当MD=MO时,如答图②所示.
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3,
∴M点的坐标为(﹣1,﹣3);
(III)当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为×4=,即AC上的点与点O之间的最小距离为.
∵>2,∴OD=OM的情况不存在.
综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
二次函数单元检测B卷
姓名:__________班级:__________考号:__________
1 、选择题(本大题共12小题 )
已知二次函数y=a(x﹣1)2+3,当x<1时,y随x的增大而增大,则a取值范围是( )
A.a≥0 B.a≤0 C.a>0 D.a<0
下列哪一个是假命题( )
A.五边形外角和为360°
B.切线垂直于经过切点的半径
C.(3,﹣2)关于y轴的对称点为(﹣3,2)
D.抛物线y=x2﹣4x+2017对称轴为直线x=2
已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2 C.x<﹣2或x>1 D.﹣2<x<1
抛物线y=(x+2)2+3的顶点坐标是( )
A.(﹣2,3) B.(2,3) C.(﹣2,﹣3) D.(2,﹣3)
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
A.t>﹣5 B.﹣5<t<3 C.3<t≤4 D.﹣5<t≤4
一次函数y=ax+b与二次函数y=ax2+bx在同一坐标系中的图象大致为( )
如图,在平面直角坐标系中,点A(0,2),在x轴上任取一点M,完成以下作图步骤:
①连接AM.作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1,l2的交点为P;
②在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线顺次连接起来,得到的曲线是( )21世纪教育网版权所有
A.直线 B.抛物线 C.双曲线 D.双曲线的一支
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
A.cm2 B.cm2 C.cm2 D.cm2
如图,在平面直角坐标系中,抛物线y=经过平移得到抛物线y=,其对称轴与两段抛物线所围成的阴影部分的面积为( )21教育网
A.2 B.4 C.8 D.16
规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);21·cn·jy·com
④若点(m,n)在反比例函数y=的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A.①② B.③④ C.②③ D.②④
2 、填空题(本大题共6小题 )
二次函数y=ax2+bx+c的图象上部分点的对应值如下表:
x ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3
y 6 0 ﹣4 ﹣6 ﹣6 ﹣4 0 6
则使y<0的x的取值范围是__________.
函数与y2=x+2的图象及交点如图所示,则不等式x2<x+2的解集是____________.
【来源:21·世纪·教育·网】
如图,在平面直角坐标系中,抛物线y=﹣x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是______.
已知抛物线y=x2+bx+c经过坐标原点,并与x轴交于A(2,0),则抛物线的表达式是 .2-1-c-n-j-y
邓老师设计了一个计算程序,输入和输出的数据如下表:
入数据 1 2 3 4 5 6 …
输出数据 …
那么,当输入数据是7时,输出的数据是 .
如图①正方形ABCD,EFGH的中心P、Q都在直线l上,EF⊥l,AC∥EH,正方形ABCD以1cm/s的速度沿直线l向正方形EFGH移动,当点A与HG的中点L重合时停止移动,设移动时间为xs时,这两个正方形重叠部分面积为ycm2,y与x的函数图象如图②,则下列结论:2①AC=4cm;②当x=3t时重叠部分的面积为7cm2;③m=s;④当P、Q重合时,重叠部分的面积为8cm2;⑤当2<x≤4时,y与x的函数关系式是y=﹣(x﹣4)2+8;
其中正确的结论的序号是 (把所有正确结论的序号都填在横线上)
3 、解答题(本大题共8小题 )
“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进了一批单价为20元的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.在义卖的过程中发现“这种文化衫每天的销售件数(件)与销售单价(元)满足一次函数关系:”.如果义卖这种文化衫每天的利润为(元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少?
把抛物线y=ax2+bx+c向左平移2个单位,同时向下平移1个单位后,恰好与抛物线y=2x2+4x+1重合.请求出a,b,c的值.2·1·c·n·j·y
已知抛物线y=ax2+bx经过点A(﹣3,﹣3)和点P(t,0),且t≠0.
(1)若该抛物线的对称轴经过点A,如图,请通过观察图象,指出此时y的最小值,并写出t的值;
(2)若t=﹣4,求a、b的值,并指出此时抛物线的开口方向;
(3)直接写出使该抛物线开口向下的t的一个值.
把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).【版权所有:21教育】
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.21教育名师原创作品
一块三角形废料如图所示,∠A=30°,∠C=90°,BC=6.用这块废料剪出一个平行四边形AGEF,其中,点G,E,F分别在AB,BC,AC上.设CE=x
(1)求x=2时,平行四边形AGEF的面积.
(2)当x为何值时,平行四边形AGEF的面积最大?最大面积是多少?
如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=﹣x2+bx+c经过B、D两点.
(1)求二次函数的解析式;
(2)连接BD,点P是抛物线上一点,直线OP把△BOD的周长分成相等的两部分,求点P的坐标.
如图1,在平面直角坐标系中,二次函数y=x2+bx的图象与x轴交于点A(6,0),△OBC的B点坐标(3,4),C点坐标为(5,0).
(1)求二次函数的关系式;
(2)将△OBC沿边BC翻折,点O落在点D,请求出点D的坐标并判断点D是否在二次函数的图象上;
(3)在(2)的条件下,如图2,点E的坐标为(0,8),有一动点P从E点出发沿EO方向以2个单位/s的速度向下运动,过点P的直线l平行于x轴,当点P运动到点O时停止运动,设运动时间为t(s),其中0≤t≤4.请探究直线l上是否存在点H,使得△ODH为直角三角形?若存在,请直接写出满足条件的点H的个数及相应t的取值范围,不需说明理由;若不存在,请说明理由.
如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0)
(1)求该抛物线的解析式.
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
答案解析
1 、选择题
1. 【分析】根据二次函数y=a(x﹣1)2+3,当x<1时,y随x的增大而增大,可以得到该二次函数的对称轴,和相应的a的值,从而可以解答本题.
解:∵二次函数y=a(x﹣1)2+3,
∴该二次函数的对称轴为直线x=1,
又∵当x<1时,y随x的增大而增大,
∴a<0,
故选D.
2. 【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解:A.五边形外角和为360°是真命题,故A不符合题意;
B、切线垂直于经过切点的半径是真命题,故B不符合题意;
C、(3,﹣2)关于y轴的对称点为(﹣3,2)是假命题,故C符合题意;
D、抛物线y=x2﹣4x+2017对称轴为直线x=2是真命题,故D不符合题意;
故选:C.
3. 【分析】先求出函数的图象与x轴的交点坐标,再根据函数的图象开口向下,即可得出当y<0时自变量x的取值范围.21·世纪*教育网
解:当y=0时,﹣x2+x+2=0,
(x+1)(﹣x+2)=0,
x1=﹣1,x2=2,
由于函数开口向下,
可知当y<0时,自变量x的取值范围是x<﹣1或x>2.
故选A
4. 【分析】抛物线y=a(x﹣h)2+k,顶点坐标是(h,k),直接根据抛物线y=(x+2)2+3写出顶点坐标则可.
解:由于y=(x+2)2+3为抛物线的顶点式,根据顶点式的坐标特点可知,抛物线的顶点坐标为(﹣2,3).
故选:A.
5. 解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4c<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确.
故选B.
6. 【分析】利用抛物线的性质解决
解:根据函数图象可知: 抛物线开口向上,所以a>o 对称抽为x-1 所以b>0,物线与y轴交于正半轴,所以c+2>2 ,c>o 所以abc>o 故①错误,
因为抛物线与x抽只有一个交点,所以b2-4a(c+2)=0,所以②错误,
因为对称抽为x=-1 所以-=-1,所以b=2a,把点(- 1,0)代入解析式得: a-b+c+2=0 ,所以a-2a+c+2=0 ,所以a=c+2 >2 所以③正确,
根据抛物线的对称性可得:当x=-2时, y=4a-2b+c+2 >2 所以4a-2b+c>0所以④正确,
因此共有③④正确,
故选B
7. 【分析】如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,利用图象法即可解决问题.
解:如图,关于x的一元二次方程﹣x2+mx﹣t=0的解就是抛物线y=﹣x2+mx与直线y=t的交点的横坐标,
当x=1时,y=3,
当x=5时,y=﹣5,
由图象可知关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,
直线y=t在直线y=﹣5和直线y=4之间包括直线y=4,
∴﹣5<t≤4.
故答案为D.
8. 【分析】对于每个选项,先根据二次函数的图象确定a和b的符号,然后根据一次函数的性质看一次函数图象的位置是否正确,若正确,说明它们可在同一坐标系内存在.
解:A.由二次函数y=ax2+bx的图象得a>0,b<0,则一次函数y=ax+b经过第一、三、四象限,且它们的交点为(1,0),所以A选项正确;
B、由二次函数y=ax2+bx的图象得a>0,b>0,则一次函数y=ax+b经过第一、二、三象限,所以B选项错误;
C、由二次函数y=ax2+bx的图象得a<0,b>0,则一次函数y=ax+b经过第一、二、四象限,所以C选项错误;
D、由二次函数y=ax2+bx的图象得a<0,b<0,则一次函数y=ax+b经过第二、三、四象限,所以D选项错误.
故选A.
9. 【分析】按照给定的作图步骤作图,根据图形中曲线的特征即可得出该曲线为抛物线.
解:根据作图步骤作图,如图所示.
由此即可得出该曲线为抛物线.
故选B/
10. 【分析】如图,由等边三角形的性质可以得出∠A=∠B=∠C=60°,由三个筝形全等就可以得出AD=BE=BF=CG=CH=AK,根据折叠后是一个三棱柱就可以得出DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO为矩形,且全等.连结AO证明△AOD≌△AOK就可以得出∠OAD=∠OAK=30°,设OD=x,则AO=2x,由勾股定理就可以求出AD=x,由矩形的面积公式就可以表示纸盒的侧面积,由二次函数的性质就可以求出结论.
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=x,
∴DE=6﹣2x,
∴纸盒侧面积=3x(6﹣2x)=﹣6x2+18x,
=﹣6(x﹣)2+,
∴当x=时,纸盒侧面积最大为.
故选C.
.
11. 解:过点C作CA⊥y,
∵抛物线y==(x2﹣4x)=(x2﹣4x+4)﹣2=(x﹣2)2﹣2,
∴顶点坐标为C(2,﹣2),
对称轴与两段抛物线所围成的阴影部分的面积为:2×2=4,
故选:B.
12. 【分析】①通过解方程得到该方程的根,结合“倍根方程”的定义进行判断;
②设x2=2x1,得到x1 x2=2x12=2,得到当x1=1时,x2=2,当x1=﹣1时,x2=﹣2,于是得到结论;【来源:21cnj*y.co*m】
③根据“倍根方程”的定义即可得到结论;
④若点(m,n)在反比例函数y=的图象上,得到mn=4,然后解方程mx2+5x+n=0即可得到正确的结论;【出处:21教育名师】
解:①由x2﹣2x﹣8=0,得
(x﹣4)(x+2)=0,
解得x1=4,x2=﹣2,
∵x1≠2x2,或x2≠2x1,
∴方程x2﹣2x﹣8=0不是倍根方程.
故①错误;
②关于x的方程x2+ax+2=0是倍根方程,
∴设x2=2x1,
∴x1 x2=2x12=2,
∴x1=±1,
当x1=1时,x2=2,
当x1=﹣1时,x2=﹣2,
∴x1+x2=﹣a=±3,
∴a=±3,故②正确;
③关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,
∴x2=2x1,
∵抛物线y=ax2﹣6ax+c的对称轴是直线x=3,
∴抛物线y=ax2﹣6ax+c与x轴的交点的坐标是(2,0)和(4,0),
故③正确;
④∵点(m,n)在反比例函数y=的图象上,
∴mn=4,
解mx2+5x+n=0得x1=﹣,x2=﹣,
∴x2=4x1,
∴关于x的方程mx2+5x+n=0不是倍根方程;
故选C.
2 、填空题
13.【分析】 根据图表信息判断出二次函数图象开口向下,然后写出函数值小于0的x的取值范围即可.21*cnjy*com
解:由表可知,抛物线开口向下,
∵x=﹣3,x=2时,y=0,
∴使y<0的x的取值范围是﹣3<x<2.
故答案为:﹣3<x<2.
14.【分析】利用函数图象得出交点坐标,利用一次函数图象只有在二次函数图象上方时,不等式x2<x+2,进而得出答案.
【解析】
利用图象得出函数与y2=x+2的图象交点坐标分别为:(-1,1)和(2,4),
∴不等式x2<x+2的解集为:-1<x<2.
故答案为:-1<x<2.
15.【分析】表示出P点坐标,进而表示出△PAB的底与高的长度,即可得出S与m的关系式,利用配方法可得△PAB的面积S的取值范围.
解:由题意,P点坐标为:(m,﹣m2+4m),
∵抛物线y=﹣x2+4x与x轴交于点O、A,
∴当y=0时,﹣x2+4x=0,
解得:x=0,或x=4,
∴A(4,0),
∴OA=4,
由题意可得:P到AB的距离为﹣m2+4m,
∴S=×4×(﹣m2+4m)=﹣2m2+8m=﹣2(m﹣2)2+8;
∵0<m<3,
∴0<S≤8.
故答案为:0<S≤8.
16.【分析】 把(0,0)代入可得出c的值,再把A(2,0)代入y=x2+bx得b的值,即可得出抛物线的表达式.
解:∵抛物线y=x2+bx+c经过坐标原点,
∴c=0,
把A(2,0)代入y=x2+bx得b=﹣2.
∴抛物线的表达式为y=x2﹣2x.
故答案为:y=x2﹣2x.
17.【分析】此题中分子的规律很好找,就是1,2,3,4,5,6…即第7次是7,但分母的规律就不好找了,这时我们可以列一个二次函数代入求.
解:从图中可以看出,分子上输入数据是n,分子就是n.
分母上我们可以列一个二次函数,可设分母为y,输入数据为x,则y=ax2+bx+c,把x=1,2,3代入代数式得:解得:
把这代入方程得:y=x2+2x﹣1,
所以当输出数据是7时,分母=49+14﹣1=62,
所以输出的数据是.
故答案为.
18.【分析】 ①由这两个正方形的重叠部分面积为8时,也就是小正方形的面积为8,求出边长即可得出AC的长;www-2-1-cnjy-com
②当2≤x≤6时,得到y与x的函数关系式,当y=7时,解方程可作判断;
③当6≤x≤8时,y与x的函数关系式为y=(8﹣x)2,此时函数y的取值范围是0≤y≤4.当y=3时,解方程即可求出m;
④由图象可得结论;
⑤当2≤x≤6时,y与x的函数关系式为y=﹣(x﹣4)2+8.
解:(1)当这两个正方形的重叠部分面积为8时,也就是小正方形的面积为8,得出小正方形的边长为2cm,所以AC=×2=4cm,故①正确.
(2)当2≤x≤6时,y与x的函数关系式为y=﹣(x﹣4)2+8,此时函数y的取值范围是4≤y≤8,当y=7时,得﹣(x﹣4)2+8=7,解得x=3或x=5.所以正方形ABCD出发3秒或5秒时,重叠部分面积为7cm2,故②正确;
(3)当0≤x≤2时,y与x的函数关系式为y=x2,此时函数y的取值范围是0≤y≤4,当y=3时,得x2=3或(8﹣x)2=3,解得x=±(负号舍去)或x=±+8(正号舍去),即m=,故③正确;
(4)由图象可以看出两个正方形的最大重叠部分面积为8,此时P、Q重合,故④正确;
(5)当2≤x≤6时,y与x的函数关系式为y=﹣(x﹣4)2+8,故⑤正确;
故答案为:①②③④⑤.
3 、解答题
19.解:每天获得的利润为:
∵
∴当销售价定为28元时,每天获得的利润最大,
最大利润是192元.
20.【分析】根据目标函数图象向相反的方向平移,可得原函数图象,根据图象右移减,上移加,可得答案.
解:将y=2x2+4x+1
整理得y=2x2+4x+1=2(x+1)2﹣1.
因为抛物线y=ax2+bx+c 向左平移2个单位,再向下平移1个单位得y=2x2+4x+1=2(x+1)2﹣1,
所以将y=2x2+4x+1=2(x+1)2﹣1向右平移2个单位,再向上平移1个单位即得y=ax2+bx+c,
故y=ax2+bx+c=2(x+1﹣2)﹣1+1=2(x﹣1)=2x2﹣4x+2,
所以a=2,b=﹣4,c=2.
21.【分析】(1)由图可以看出A点为抛物线的顶点,且开口向上,所以此点即为此函数的最小值;
(2)点p是抛物线与x轴的一个交点,而此时另一个交点是0,那么P与O是关于抛物线对称轴的两个对称点,知道了对称点的坐标,就很容易求出t的值;
(3)a>0时,抛物线的开口向上,a<0时,抛物线的开口向下,求出a的值就知道其开口方向.
解:(1)∵抛物线的对称轴经过点A,
∴A点为抛物线的顶点,
∴y的最小值为﹣3,
∵P点和O点对称,
∴t=﹣6;
(2)分别将(﹣4,0)和(﹣3,﹣3)代入y=ax2+bx,得:,
解得,
∴抛物线开口方向向上;
(3)将A(﹣3,﹣3)和点P(t,0)代入y=ax2+bx,
,
由①得,b=3a+1③,
把③代入②,得at2+t(3a+1)=0,
∵t≠0,∴at+3a+1=0,
∴a=﹣.
∵抛物线开口向下,∴a<0,
∴﹣<0,
∴t+3>0,
∴t>﹣3.
故t的值可以是﹣1(答案不唯一).
(注:写出t>﹣3且t≠0或其中任意一个数均给分)
22.【分析】(1)将t=3代入解析式可得;
(2)根据h=10可得关于t的一元二次方程,解方程即可;
(3)由题意可得方程20t﹣t2=m 的两个不相等的实数根,由根的判别式即可得m的范围.
解:(1)当t=3时,h=20t﹣5t2=20×3﹣5×9=15(米),
∴当t=3时,足球距离地面的高度为15米;
(2)∵h=10,
∴20t﹣5t2=10,即t2﹣4t+2=0,
解得:t=2+或t=2﹣,
故经过2+或2﹣时,足球距离地面的高度为10米;
(3)∵m≥0,由题意得t1,t2是方程20t﹣5t2=m 的两个不相等的实数根,
∴b2﹣4ac=202﹣20m>0,
∴m<20,
故m的取值范围是0≤m<20.
23.【分析】设平行四边形AGEF的面积是S.利用平行四边形AGEF的对边互相平行知EF∥AG,所以同位角∠A=∠CFE=30°;然后在直角三角形ABC和直角三角形BEF中利用锐角三角函数的定义求得CF、AC的长度,从而求得平行四边形AGEF的底边AF=AC﹣CF;最后根据平行四边形的面积公式S=底×高得出关于S与x的函数关系式S=﹣x2+6x;21cnjy.com
(1)将x=2代入S与x的函数关系式S=﹣x2+6x,并求解即可;
(2)利用配方法求二次函数的最值.
解:设平行四边形AGEF的面积是S.
∵四边形AGEF是平行四边形,
∴EF∥AG;
∵∠A=30°,∠C=90°,CE=x,BC=6,
∴∠A=∠CFE=30°,
∴CF=x,AC=6,
∴AF=6﹣x;
∴S=AF CE=(6﹣x)x=﹣x2+6x,即S=﹣x2+6x;
(1)当x=2时,S=﹣4+12=8,即S=8.
答:平行四边形AGEF的面积为(平方单位)
(2)由S=﹣x2+6x,得
,
∴,
∴当x=3时,平行四边形AGEF的面积最大,最大面积是(平方单位)
24.【分析】(1)由旋转性质可得CD=AB=1、OA=OC=2,从而得出点B、D坐标,代入解析式即可得出答案;
(2)由直线OP把△BOD的周长分成相等的两部分且OB=OD,知DQ=BQ,即点Q为BD的中点,从而得出点Q坐标,求得直线OP解析式,代入抛物线解析式可得点P坐标.
解:(1)∵Rt△AOB绕点O逆时针旋转90°得到Rt△COD,
∴CD=AB=1、OA=OC=2,
则点B(2,1)、D(﹣1,2),代入解析式,得:
,
解得:,
∴二次函数的解析式为y=﹣x2+x+;
(2)如图,
∵直线OP把△BOD的周长分成相等的两部分,且OB=OD,
∴DQ=BQ,即点Q为BD的中点,
∴点Q坐标为(,),
设直线OP解析式为y=kx,
将点Q坐标代入,得: k=,
解得:k=3,
∴直线OP的解析式为y=3x,
代入y=﹣x2+x+,得:﹣ x2+x+=3x,
解得:x=1或x=﹣4(舍),
当x=1时,y=3,
∴点P坐标为(1,3).
25.【分析】(1)把A点坐标代入y=x2+bx,求出b的值,即可求出二次函数的关系式.
(2)首先由B、C坐标证得OB=OC,再根据翻折的性质可证得四边形OBDC为菱形,进而判断出四边形BMND是矩形,所以MN=BD=5,DN=BM=4,ON=OM+MN=3+5=8,据此求出点D的坐标,然后把点D的坐标代入抛物线解析式,即可判断出点D是否在二次函数的图象上.www.21-cn-jy.com
(3)首先求出当l和BD重合时,l和x轴重合时,t的值各是多少;然后分类讨论:①当0≤t<3﹣,t=2或t=4时;②当t=3﹣时;③当3﹣<t<2,或2<t<4时;根据△ODH为直角三角形,写出所有满足条件的点H的个数及相应t的取值范围即可.
解:(1)将点A(6,0)代入y=x2+bx,可得
0=+6b,
解得b=﹣,
∴二次函数的关系式是y=x2﹣x.
(2)如图1,过点B作BM⊥x轴于点M,过点D作DN⊥x轴于点N,
,
将△OBC沿边BC翻折,点O落在点D,
∵△OBC的B点坐标(3,4),C点坐标为(5,0),
∴OM=3,BM=4,OC=5,
∴OB=,
∴OB=OC,
∵将△OBC沿边BC翻折得到△DBC,
∴△OBC≌△DBC,
∴OB=DB,OC=DC,
又∵OB=OC,
∴OB=DB=OC=DC,
∴四边形OBDC是菱形,
∴BD∥x轴,
∵BM⊥x轴,DN⊥x轴,
∴BM∥DN,
∴四边形BMND是平行四边形,
∵∠BMN=90°,
∴四边形BMND是矩形,
∴MN=BD=5,DN=BM=4,
∴ON=OM+MN=3+5=8,
∴点D的坐标是(8,4),
∵当x=8时,y=×82﹣×8=4,
∴点D是否在二次函数的图象上.
(3)由(2)可得四边形OBDC是菱形,
∴BD∥x轴,
当l和BD重合时,
∵8﹣2t=4,
∴t=2,点H的个数是2个;
当l和x轴重合时,
∵8﹣2t=0,
∴t=4,点H的个数是2个;
①当0≤t<3﹣,t=2或t=4时,
点H的个数是2个.
②当t=3﹣时,
点H的个数是3个.
③当3﹣<t<2,或2<t<4时,
点H的个数是4个.
26.解:(1)把点C(0,﹣4),B(2,0)分别代入y=x2+bx+c中,
得,
解得
∴该抛物线的解析式为y=x2+x﹣4.
(2)令y=0,即x2+x﹣4=0,解得x1=﹣4,x2=2,
∴A(﹣4,0),S△ABC=AB OC=12.
设P点坐标为(x,0),则PB=2﹣x.
∵PE∥AC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△PBE∽△ABC,
∴,即,
化简得:S△PBE=(2﹣x)2.
S△PCE=S△PCB﹣S△PBE=PB OC﹣S△PBE=×(2﹣x)×4﹣(2﹣x)2
=x2﹣x+
=(x+1)2+3
∴当x=﹣1时,S△PCE的最大值为3.
(3)△OMD为等腰三角形,可能有三种情形:(I)当DM=DO时,如答图①所示.
DO=DM=DA=2,
∴∠OAC=∠AMD=45°,
∴∠ADM=90°,
∴M点的坐标为(﹣2,﹣2);
(II)当MD=MO时,如答图②所示.
过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=1,AN=AD+DN=3,
又△AMN为等腰直角三角形,∴MN=AN=3,
∴M点的坐标为(﹣1,﹣3);
(III)当OD=OM时,
∵△OAC为等腰直角三角形,
∴点O到AC的距离为×4=,即AC上的点与点O之间的最小距离为.
∵>2,∴OD=OM的情况不存在.
综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
