24.3 正多边形与圆学案(附答案)
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
24.3 正多边形和圆
知识梳理
1.① 相等, 也相等的多边形叫做正多边形.
②一个正多边形的外接圆 叫做这个正多边形的中心.正多边形的中心到正多边形 的距离相等.
③正多边形外接圆的 叫做正多边形的半径(用R)表示.
④正多边形每一边所对的 叫做正多边形的中心角。
⑤中心到正多边形一边的 叫做正多边的边心距。边心距r实质上也是正多边形内切圆的 .
2.把一个圆分成n等份,连接各点所得到的多边形是 .
3.正n边形的半径为R,边心距为r,边长为a,
(1)中心角的度数为: .
(2)每个内角的度数为: 或 .
(3)每个外角的度数为: .
(4)周长为:_ _,面积为: .
4.正n边形都是 图形,当边数为偶数时,它的对称轴有_____条,并且还是 图形;当边数为奇数时,它只是 图形.(填“轴对称图形”或“中心对称图形”)
重点突破
知识点 正多边形和圆
1.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.3,3 C.6,3 D.6, 3
【解析】本题主要考查正多边形和圆,重点是了解有关概念,并熟悉如何构造特殊的直角三角形.
∵正方形的边长为6,OE⊥AD于点E∴AE=AD=3,∠AEO=90°,∠AOE=45°
∴OE=AE=3∴,故选B.
【答案】B
2.正十二边形每个内角的度数为 .
【解析】本题主要考查的是正十二边形的每个内角都相等,每个外角也相等,熟练掌握相关计算是解本题的关键.求正多边形的内角有两种求法:1.根据多边形内角和定理:(n﹣2) 180°(n≥3且n为正整数)求出内角和,然后再计算一个内角的度数.2.直接利用多边形外角和求其外角度数.利用外角与内角互补的关系求内角的度数,即每一个内角的度数为150°.
【答案】150°
基础过关
1.如果一个正多边形的中心角为72°,那么这个正多边形的边数是( )
A、4 B、5 C、6 D、7
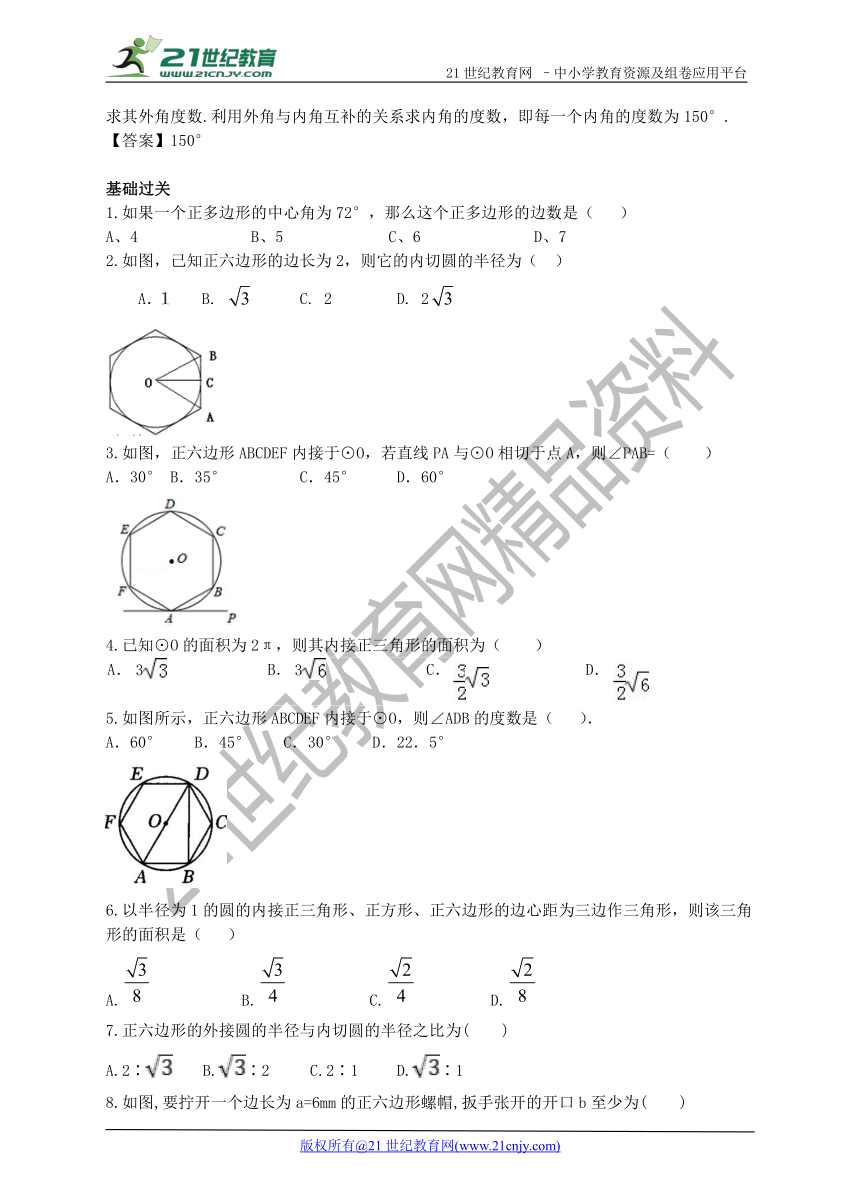
2.如图,己知正六边形的边长为2,则它的内切圆的半径为( )
A. B. C. 2 D. 2
3.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
A.30° B.35° C.45° D.60°
( http: / / www." \o "中国教育出版网\ )
4.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A. 3 B. 3 C. D.
5.如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( ).
A.60° B.45° C.30° D.22.5°
6.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
7.正六边形的外接圆的半径与内切圆的半径之比为( )
A.2∶ B.∶2 C.2∶1 D.∶1
8.如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为( )
A.6mm B.12mm C.6mm D.4mm
9.如果一个正多边形的一个内角为144°,则这个正多边形的边数为 .
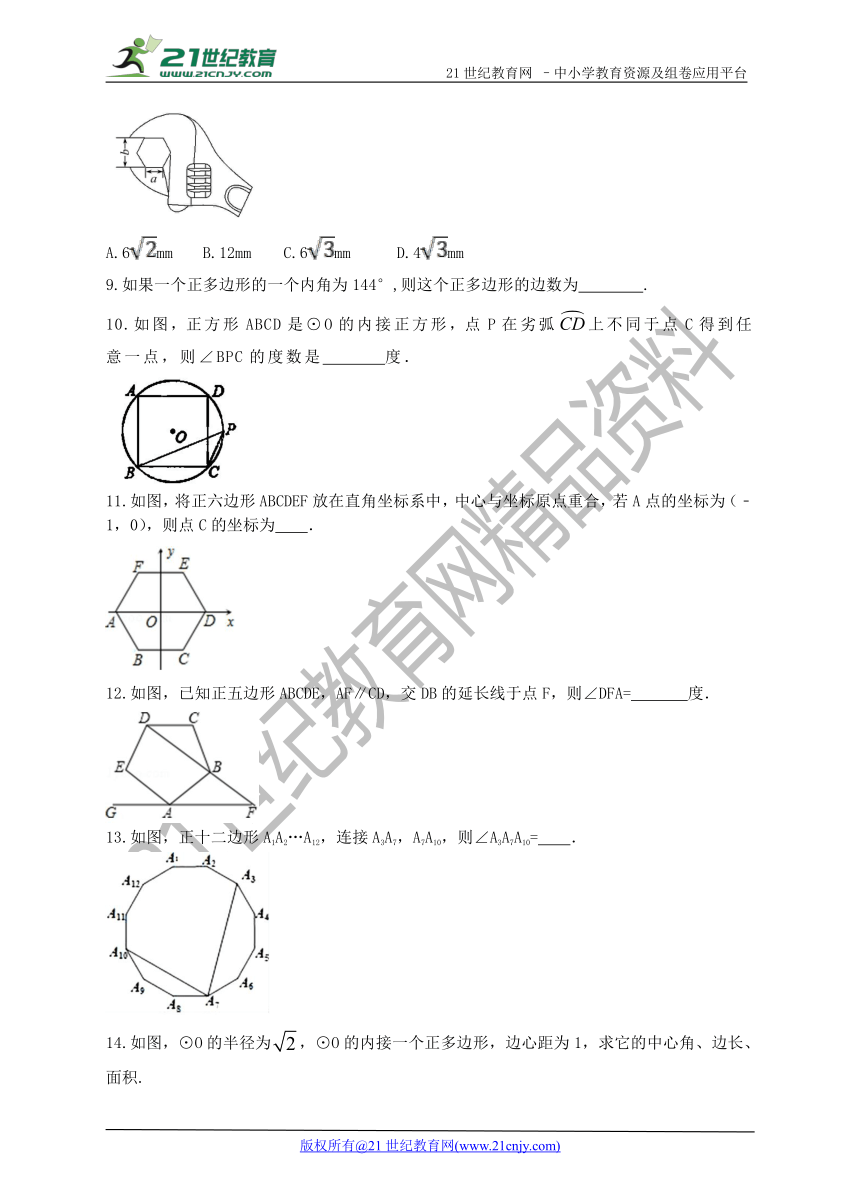
10.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C得到任意一点,则∠BPC的度数是 度.
11.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为 .
12.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA= 度.
13.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10= .
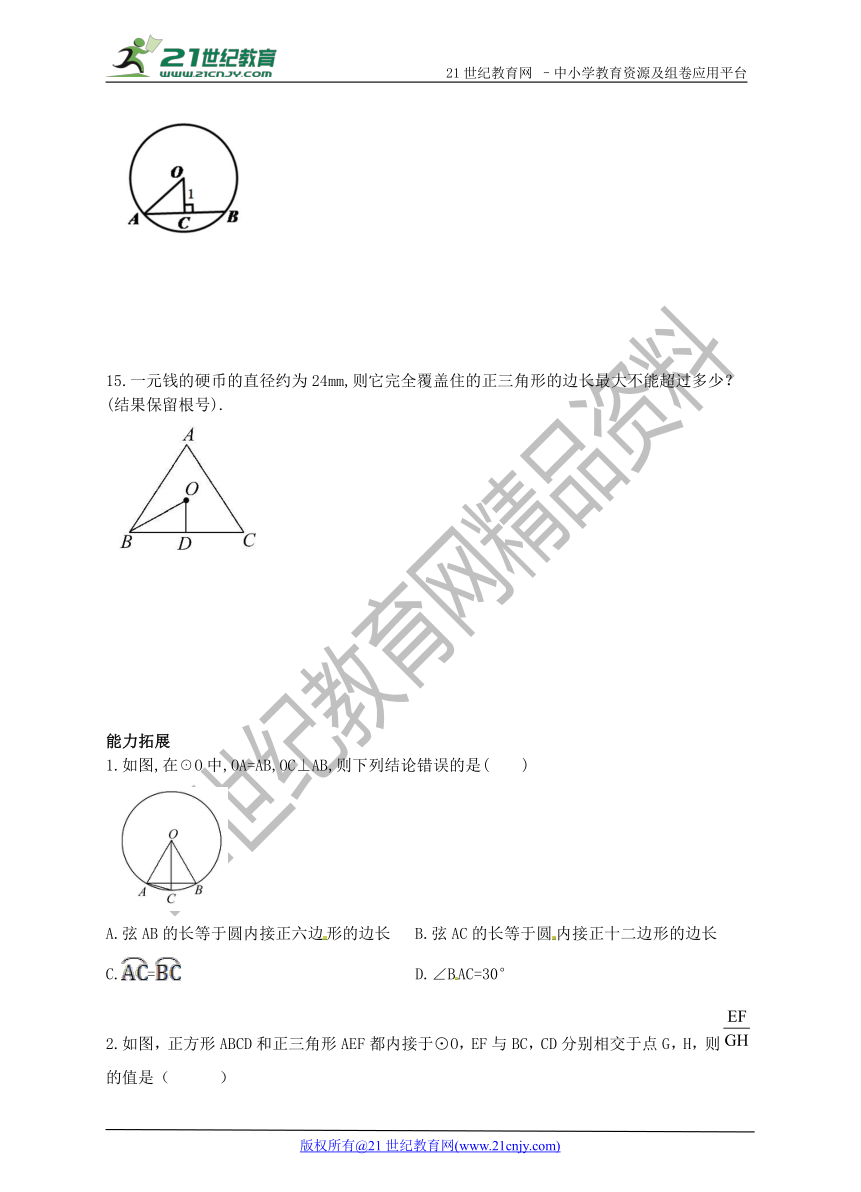
14.如图,⊙O的半径为,⊙O的内接一个正多边形,边心距为1,求它的中心角、边长、面积.
15.一元钱的硬币的直径约为24mm,则它完全覆盖住的正三角形的边长最大不能超过多少?(结果保留根号).
能力拓展
1.如图,在☉O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长 B.弦AC的长等于圆内接正十二边形的边长
C.= D.∠BAC=30°
2.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则 HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.DSMT4 的值是( )
( http: / / www." \o "中国教育出版网\ )
A. HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.3 B. HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.3 C. HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.3 D. 2
3.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
4.如图(1),(2),(3),…,(n),M,N分别是☉O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB,BC上的点,且BM=CN,连接OM、ON.
(1)求图(1)中∠MON的度数.
(2)图(2)中∠MON的度数是 ,图(3)中∠MON的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案
知识梳理
1.各边,各角;圆心,各个顶点;半径;圆心角;距离,半径.
2.正n多边形.
3.;180°-,;;na,
4.轴对称,n,中心对称,轴对称
基础过关
1.B
2.B
3.A
4.C
5.C
6.D
7.A
8.C
9.十
10.45
11. )
12.36
13.75°
14.解:连结OB
∵在Rt△AOC中,AC==1
∴AC=OC ∴∠AOC=∠OAC=45°
∵OA=OB OC⊥AB
∴AB=2AC=2 ∠AOB=2∠OAC=2×45°=90°
∴这个内接正多边形是正方形.
∴面积为22=4
∴中心角为90°,边长为2,面积为4.
15.解:如图,已知此圆半径为12mm,则OB=12mm.在直角△OBD中,∠BOD=60°,
∴∠OBD=30°,∴OD=6mm,BD==6mm.
∴BC=12mm.
∴它完全覆盖住的正三角形的边长最大不能超过12mm。
能力拓展
1.D
2.C
3.
4.(1)解:方法一:连结OB、OC.
∵正△ABC内接于⊙O,
∴∠OBM=∠OCN=30°,
∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN(SAS).
∴∠BOM=∠CON.
∴∠MON=∠BOC=120°.
方法二:连结OA、OB.
∵正△ABC内接于⊙O,
∴AB=AC,∠OAM=∠OBN=30°,
∠AOB=120°.
又∵BM=CN,
∴AM=BN.
又∵OA=OB,
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
24.3 正多边形和圆
知识梳理
1.① 相等, 也相等的多边形叫做正多边形.
②一个正多边形的外接圆 叫做这个正多边形的中心.正多边形的中心到正多边形 的距离相等.
③正多边形外接圆的 叫做正多边形的半径(用R)表示.
④正多边形每一边所对的 叫做正多边形的中心角。
⑤中心到正多边形一边的 叫做正多边的边心距。边心距r实质上也是正多边形内切圆的 .
2.把一个圆分成n等份,连接各点所得到的多边形是 .
3.正n边形的半径为R,边心距为r,边长为a,
(1)中心角的度数为: .
(2)每个内角的度数为: 或 .
(3)每个外角的度数为: .
(4)周长为:_ _,面积为: .
4.正n边形都是 图形,当边数为偶数时,它的对称轴有_____条,并且还是 图形;当边数为奇数时,它只是 图形.(填“轴对称图形”或“中心对称图形”)
重点突破
知识点 正多边形和圆
1.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6,3 B.3,3 C.6,3 D.6, 3
【解析】本题主要考查正多边形和圆,重点是了解有关概念,并熟悉如何构造特殊的直角三角形.
∵正方形的边长为6,OE⊥AD于点E∴AE=AD=3,∠AEO=90°,∠AOE=45°
∴OE=AE=3∴,故选B.
【答案】B
2.正十二边形每个内角的度数为 .
【解析】本题主要考查的是正十二边形的每个内角都相等,每个外角也相等,熟练掌握相关计算是解本题的关键.求正多边形的内角有两种求法:1.根据多边形内角和定理:(n﹣2) 180°(n≥3且n为正整数)求出内角和,然后再计算一个内角的度数.2.直接利用多边形外角和求其外角度数.利用外角与内角互补的关系求内角的度数,即每一个内角的度数为150°.
【答案】150°
基础过关
1.如果一个正多边形的中心角为72°,那么这个正多边形的边数是( )
A、4 B、5 C、6 D、7
2.如图,己知正六边形的边长为2,则它的内切圆的半径为( )
A. B. C. 2 D. 2
3.如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
A.30° B.35° C.45° D.60°
( http: / / www." \o "中国教育出版网\ )
4.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A. 3 B. 3 C. D.
5.如图所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是( ).
A.60° B.45° C.30° D.22.5°
6.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A. B. C. D.
7.正六边形的外接圆的半径与内切圆的半径之比为( )
A.2∶ B.∶2 C.2∶1 D.∶1
8.如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为( )
A.6mm B.12mm C.6mm D.4mm
9.如果一个正多边形的一个内角为144°,则这个正多边形的边数为 .
10.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C得到任意一点,则∠BPC的度数是 度.
11.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为 .
12.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA= 度.
13.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10= .
14.如图,⊙O的半径为,⊙O的内接一个正多边形,边心距为1,求它的中心角、边长、面积.
15.一元钱的硬币的直径约为24mm,则它完全覆盖住的正三角形的边长最大不能超过多少?(结果保留根号).
能力拓展
1.如图,在☉O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长 B.弦AC的长等于圆内接正十二边形的边长
C.= D.∠BAC=30°
2.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则 HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.DSMT4 的值是( )
( http: / / www." \o "中国教育出版网\ )
A. HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.3 B. HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.3 C. HYPERLINK "http://www." \o "中国教育出版网\" EMBED Equation.3 D. 2
3.如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为 .
4.如图(1),(2),(3),…,(n),M,N分别是☉O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB,BC上的点,且BM=CN,连接OM、ON.
(1)求图(1)中∠MON的度数.
(2)图(2)中∠MON的度数是 ,图(3)中∠MON的度数是 .
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
参考答案
知识梳理
1.各边,各角;圆心,各个顶点;半径;圆心角;距离,半径.
2.正n多边形.
3.;180°-,;;na,
4.轴对称,n,中心对称,轴对称
基础过关
1.B
2.B
3.A
4.C
5.C
6.D
7.A
8.C
9.十
10.45
11. )
12.36
13.75°
14.解:连结OB
∵在Rt△AOC中,AC==1
∴AC=OC ∴∠AOC=∠OAC=45°
∵OA=OB OC⊥AB
∴AB=2AC=2 ∠AOB=2∠OAC=2×45°=90°
∴这个内接正多边形是正方形.
∴面积为22=4
∴中心角为90°,边长为2,面积为4.
15.解:如图,已知此圆半径为12mm,则OB=12mm.在直角△OBD中,∠BOD=60°,
∴∠OBD=30°,∴OD=6mm,BD==6mm.
∴BC=12mm.
∴它完全覆盖住的正三角形的边长最大不能超过12mm。
能力拓展
1.D
2.C
3.
4.(1)解:方法一:连结OB、OC.
∵正△ABC内接于⊙O,
∴∠OBM=∠OCN=30°,
∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN(SAS).
∴∠BOM=∠CON.
∴∠MON=∠BOC=120°.
方法二:连结OA、OB.
∵正△ABC内接于⊙O,
∴AB=AC,∠OAM=∠OBN=30°,
∠AOB=120°.
又∵BM=CN,
∴AM=BN.
又∵OA=OB,
∴△AOM≌△BON(SAS).
∴∠AOM=∠BON.
∴∠MON=∠AOB=120°.
(2)90° 72°
(3)∠MON=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
