第十五章《分式》导学案

15.1.1
从分数到分式
新授课
主备：韩树军
审核：张万双
时间：
班级：
姓名：
学教目标：
1.了解分式的概念以及分式与整式概念的区别与联系.
2.掌握分式有意义的条件，进一步理解用字母表示数的意义，发展符号感.
3.以描述实际问题中的数量关系为背景，体会分式是刻画现实生活中数量关系的一类代数式.
学教重点：
分式的概念和分式有意义的条件.
学教难点：
分式的特点和分式有意义的条件.
一、预习内容：
1.什么是整式？
，整式中如有分母，
分母中
（含、不含）字母
2.下列各式中，哪些是整式？哪些不是整式？两者有什么区别？
；2x+y
；
；
；
；3a
；5
.
3.阅读“引言”，
“引言”中出现的式子是整式吗？
4.自主探究：完成p127的“思考”，通过探究发现，
、、、与分数一样，都是
的形式，分数的分子A与分母B都是
，并且B中都含有
.
二、数学概念:
1.归纳：分式的意义：
.
代数式
、、
、、、都是
.分数有意义的条件是
.那么分式有意义的条件是
.
分式：
三、例题讲解：
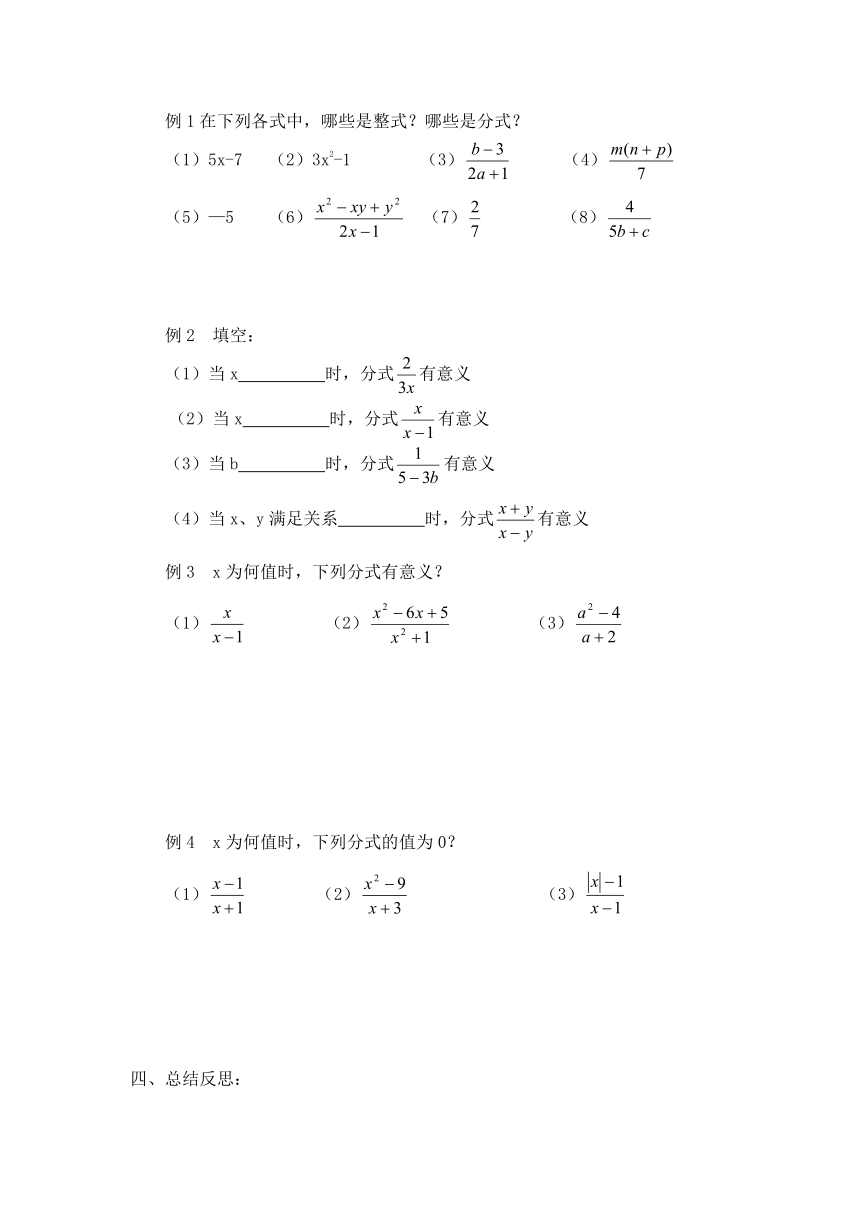
例1在下列各式中，哪些是整式？哪些是分式？
（1）5x-7
（2）3x2-1
（3）
（4）
（5）—5
（6）
（7）
（8）
例2
填空：
当x
时，分式有意义
（2）当x
时，分式有意义
（3）当b
时，分式有意义
（4）当x、y满足关系
时，分式有意义
例3
x为何值时，下列分式有意义？
（1）
（2）
（3）
例4
x为何值时，下列分式的值为0？
（1）
（2）
（3）
四、总结反思：
说说你的收获；
你还有什么问题？
五、反馈练习：
1.下列各式中，（1）（2）（3）（4）（5）（6）0
（7）（x+y）整式是
，分式是
.（只填序号）
2.当x=
时，分式没有意义.
3.当x=
时，分式的值为0
.
4.当x=
时，分式的值为正，当x=
时，分式的值为非负数.
六、提升能力
1.甲,乙两人分别从两地同时出发,若相向而行,则小时相遇;若同而行则
小时甲追上乙,那么甲的速度是乙的速度的（　）倍.
Ａ.　　　Ｂ.　　　　Ｃ.　　　Ｄ.
2.“循环赛”是指参赛选手间都要互相比赛一次的比赛方式．如果一次乒乓球比赛有x名选手报名参加，比赛方式采用“循环赛”，那么这次乒乓球比赛共有
场.
3.使分式没有意义的x的取值是（
）
A.―3
B.―2
C.
3或―2
D.
±3
七、作业布置：
15.1.2分式的基本性质（1）
新授课
主备：韩树军
审核：张万双
时间：
班级：
姓名：
学习目标：
1.理解并掌握分式的基本性质，能进行分式的等值变形.
2.进一步理解分式的基本性质，并能用其进行分式的约分.
3.了解最简分式的意义，并能把分式化成最简分式.
教学重点：
1.分式的基本性质及其应用.
2.分式的约分.
教学难点：
1.利用分式的基本性质，判断分式是否有意义.
2.利用分式的基本性质把分式化成最简分式.
一、预习内容
1.小学里学过的分数的基本性质的内容是什么？
由分数的基本性质可知，如数c≠0,那么，
2.你能通过分数的基本性质猜想分式的基本性质吗？试一试归纳：分式的基本性质：
用式子表示为
3.分解因式（1）x2-2x
=
（2）3x2+3xy=
（3）a2-4=
(4)
a2-4ab+b2=
二、数学概念
1.约分：
2.最简分式：
三、例题讲解：
1.例1
填空：
（1），
（2），
2.约分：
（1）
（2）
（3）
3.填空：（1）
（2）
4.例3下列分式的变形是否正确？为什么？
（1）
（2）
5.例4不改变分式的值，使分式的分子与分母各项的系数化为整数
四、总结反思：
说说你的收获：
你还有什么问题？
五、反馈练习：
1、不改变分式的值，使下列分式的分子与分母都不含“—”号：
（1）、
（2）、
（3）、
（4）—
（5）
（6）—
2、不改变分式的值，使下列分式的分子与分母都不含“—”号：
（1）=
、（2）—=
。
3、填空：（1）=（2）
、（3）
六、能力提升：
1、若把分式中的x、y都扩大3倍，那么分式的值是
。
2、不改变分式的值，使下列分式的分子与分母的最高次项的系数化为正数。
（1）
（2）
（3）。
3、
下列各式的变形中，正确的是（
）
A.
B.
C.
D.
4、
下面两位同学做的两种变形,请你判断正误,并说明理由.
甲生：;
乙生：
七、作业布置：
1、p132，1题
2、p133，，，1、2、3、4、5、6、8题
15.1.2分式的基本性质（2）
新授课
主备：张万双
审核：张万双
时间：
班级：
姓名：
学习目标：
1.了解分式通分的步骤和依据.
2.掌握分式通分的方法.
3.经历探索分式通分的方法的过程,发展学生实践能力和合作意识.
学习重点和难点
重点：掌握分式的通分方法
难点：准确找出不同分母的分式的最简公分母
一、预习内容
1.分式的基本性质的内容是
用式子表示
2.把异分母分数，化成同分母分数.把异分母分数化成同分母分数的，根据是什么？你认为通分的关键是什么？
3.阅读课本P131
～132
页，思考下列问题：
（1）什么叫分式的通分？与分数通分有什么不同？
（2）如何确定最简公分母
二、数学概念
通分的定义：把几个异分母分式分别化成
最简公分母：
三、例题讲解
1.通分：（根据前面的内容小组讨论完成，小组汇报）
（1）与
（2）与；
（3）
与
2.怎样确定最简公分母？
3.通分
（1）与
（2）与（3）与
四.总结反思
1.这节课你都学到了什么？
2.本节课你对自己最满意的一件事是：
本节课你对自己最不满意的一件事是：
五、反馈练习
1.分式的最简公分母是（
）.
（A）24a2b3
(B)24ab2(C)12ab2(D)12a2b3
2.分式的最简公分母是（
）
（A）　(B)　
(C)　(D)
3.通分
（1）与；
（2）与.
六、能力提升
加大难度，你能行
通分：（1）
（2）
作业布置
1.课本P133页习题15.1第7题（写到作业本上）
2.质量检测通分练习题
15．2．1分式的乘除(第一课时)
新授课
主备：赵淑明
审核：李绍柱
时间：
班级：
姓名：
学习目标：1、理解分式乘除法的法则.
2、会进行分式乘除运算.
3．渗透类比转化的数学思想方法．
学习重点和难点
重点：会用分式乘除的法则进行运算.
难点：灵活运用分式乘除的法则进行运算.
一、预习内容
（一）引入问题（只列算式）
1.一个水平放置的长方体容器，其体积为v，底面长为a，宽为b，当容器内的水占容积的时，水面的高度为______.
2.大拖拉机m天耕地a公顷，小拖拉机n天耕地b公顷，大拖拉机的工作效率是小拖拉机工作效率的_____倍.
（二）类比联想
在小学我们学习过分数的乘除法运算，请同学们下面的运算.
____=_____
2.____=_____
回忆：分数的乘法法则:__________________________________
分数的除法法则:__________________________________
二、数学模型
类似于分数的乘除法，分式有：
乘法法则：_____;
除法法则：_____=______
三、例题讲解
学过了分式的乘除法运算法则，下面我们来共同研究一下它们在具体问题中的应用.
例1.
计算
（2）
例2.
计算
(2)
四、总结反思
1、说说你的收获
2、你还有什么问题？
五、反馈练习
完成预习导学（一）中的计算.
2.计算：
(1)
(2)
(3)
(4)
六、能力提升：
计算
(1）
(2)
七、作业布置
15.2.1分式的乘除（第二课时）新授课
主备：马振会
审核：赵淑明
时间：
班级：
姓名：
学习目标：1、熟练地进行分式乘除法的混合运算
2、
运用转化思想，将乘除混合运算统一为乘法运算
3、经历转化过程，感受事物间辩证统一的相互关系
学习重点和难点：
重点：熟练地进行分式乘除法的混合运算.
难点：熟练地进行分式乘除法的混合运算.
一、预习内容：
我们已经学过分式的乘法和除法运算，你能写出分式的乘法和除法运算的法则吗？
2、因式分解方法：
（1）提公因式法：系数找
公因式：字母找
相同字母指数取
（2）公式法：
1）平方差公式：
2）完全平方公式:
3、约分
（1）当分子、分母为单项式时
，约分步骤：①②
（2）当分子、分母为多项式时，约分步骤：
①②
③
约分：（1）-
（2）
（4）
二、数学模型
分式乘除法的混合运算先把除法统一成运算，再把分子、分母中能因式分解的多项式，最后进行，注意最后的结果要求最简.
三、例题讲解
例
计算
(1)
(2)
四、总结反思
说说你的收获.
你还有什么问题？
五、反馈练习
计算：
(1)
（2）
（3）
（4）
六、能力提升
课堂上，吴老师给大家出了这样一道题：求当x等于（1）7－2；（2）9+2时，请分别计算代数式÷的值．小明一看，“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？
七、作业布置
15．2．1分式的乘除(第三课时)
新授课
主备：刘凯
审核：李绍柱
时间：
班级：
姓名：
学习目标：
理解分式乘方的运算法则，熟练地进行分式乘方的运算.
学习重点和难点
重点：熟练地进行分式乘方的运算.
难点：熟练地进行分式乘、除、乘方的混合运算.
一、预习内容：
1.幂的有关运算公式：（1）同底数幂的乘法
（2）同底数幂的除法
（3）幂的乘方
（4）积的乘方
2.
计算（1）(x4)3·x7
（2）
（3）(-6a4b2)·(-2a)2
（4）
3.你能根据乘方的意义和分式乘法的法则写出下列各式的结果吗？
；
；
；
.
二、数学模型
分式的乘方法则：
.
三、例题讲解
例1.计算
（1）；
（2）
例2计算：
（1）
(2)
四、总结反思
1.说说你的收获.
2.你还有什么问题？
五、反馈练习：
计算下列各题
（1）（）2÷（）·（-）3
（2）（）2·（）3÷（-）4
（3）（）2·（）·（）3
（4）
六、能力提升
加点难度你还能完成吗？
计算：
七、作业布置
15.2.2分式的加减（第一课时）
新授课
主备：王艳辉
审核：赵淑明
时间：
班级：
姓名：
学习目标：1、熟练地进行同分母的分式加减法的运算.
2、会把异分母的分式通分，转化成同分母的分式相加减.
3、渗透类比转化的数学思想方法.
学习重点和难点：
重点：熟练地进行异分母的分式加减法的运算.
难点：熟练地进行异分母的分式加减法的运算.
预习内容：
我们已经学过分数的加减法运算，你能写出分数的加减法运算的法则吗？
、
、
的最简公分母是
.
最简公分母的确定方法
.
你能写出下面式子的计算结果吗？
①
+
②-
③-
④+
大胆猜一猜：分式的加减法法则和分数的加减法法则
（是、否）相同.
你能计算下面这些式子吗？祝你成功！
-
（2）-
二、数学模型
分式加减法法则：______________________________________________________________
三、例题讲解
例
计算
+-
（2）+
四、总结反思
说说你的收获
你还有什么问题？
五、反馈练习
计算：（1）-+
（2）+-
-
（4）-
六、能力提升
加点难度，你还能完成吗？
=+
七、作业布置
15．2．2分式的加减（第二课时）
新授课
主备：李绍柱
审核：赵淑明
时间：
班级：
姓名：
学习目标：1、明确分式混合运算的顺序.
2、熟练地进行分式的混合运算.
3、渗透类比转化的数学思想方法．
学习重点和难点
重点：熟练地进行分式的混合运算.
难点：熟练地进行分式的混合运算.
一、预习内容
1、我们已经学过分数的混合运算，你能学出分数混合运算的顺序吗？
2、你能写出下面式子的计算结果吗？
(1)
(2)
3、大胆猜一猜：分式混合运算的顺序和分数混合运算的顺序____（是、否）相同.
4、你能计算下面这些式子吗？祝你成功！
（1）
（2）
二、数学模型
分式混合运算的顺序是
三、例题讲解
例
计算
（1）
（2）
四、总结反思
1、说说你的收获
2、你还有什么问题？
五、反馈练习
计算：（1）
（2）
(3)
(4)
六、能力提升
加点难度，你还能完成吗？
先化简：，当时，再从的范围内选取一个合适的整数代入求值.
七、作业布置
15．2．3整数指数幂
新授课
主备：李绍柱
审核：赵淑明
时间：
班级:
姓名：
学习目标：
1．知道负整数指数幂=（a≠0，n是正整数）.
2．掌握整数指数幂的运算性质.
3．会用科学计数法表示小于1的数.
学习重点和难点
重点：掌握整数指数幂的运算性质.
难点：会用科学计数法表示小于1的数.
一、预习内容
1、回忆正整数指数幂的运算性质：
（1）同底数的幂的乘法：(m,n是正整数)；
（2）幂的乘方：(m,n是正整数)；
（3）积的乘方：(n是正整数)；
（4）同底数的幂的除法：(
a≠0，m,n是正整数，m＞n)；
（5）商的乘方：(n是正整数)；
（6）0指数幂的规定，即当a≠0时，.
2、根据上述性质，你能计算下面这些式子吗？祝你成功！
（1）（2）（3）（4）
（5）若
3、探究：观察第四条性质，是否必须要求m＞n？当m=n或m在中，当m=n时，产生0次幂，即当时，，那么当时，会产生什么样的情况呢？
（1）计算，，由此得出：_________
（2）当时，，，由此得出：__________（）
（3）当，m是正整数时，，由此得出：__________________
观察上面三个问题所得结果，你能得出什么结论？
二、数学模型
负整数指数幂的意义：当n时正整数时，().
追问：指数是负数的意思是什么？是取相反数吗？
这就是说：是的倒数.例如，
追问：为什么要求呢？
三、例题讲解
例1、填空：
（1），，
（2），，
（3），，
（4）
例2、把下列各式转化为只含有正整数指数幂的形式
（1）
（2）
（3）
例3、利用负整数指数幂把下列各式化为不含分母的形式
（1）
（2）
（3）
四、反馈练习
计算：（1）
（2）
（3）
五、科学记数法
我们已经知道，一些较大的数适合用科学记数法表示.例如：光速约为米/秒，太阳的半径约为千米.
有了负整数指数幂后，小于1的正数也可以用科学记数法表示.例如：，
即小于1的正数可以用科学记数法表示为的形式，其中是整数数位只有一位的正数，n是正整数.
练习：
1、用科学记数法表示下列各数：
0.000000001
0.0012
0.000000345
-0.00003
0.0000000108
2、计算：
（1）
（2）
六、总结反思
1、说说你的收获
2、你还有什么问题？
七、能力提升
加点难度，你还能完成吗？
1、计算：
2、已知：，求
八、布置作业
15.3
分式方程（1）
新授课
主备：
陈树山
审核：甄玉秋
时间：
班级：
学习目标
1、知道分式方程的概念能识别分式方程．
2、会用去分母的方法解可化为一元一次方程的分式方程，体会化归思想和程序化思想．
3、了解对分式方程的解进行检验的原因.
学习重点和难点
重点：利用去分母的方法解分式方程．
难点：检验分式方程解的原因
预习内容
1.前面我们已经学习了哪些方程？是怎样的方程？如何求解？
（1）前面我们已经学过了
方程.
（2）一元一次方程是
方程.
（3）一元一次方程的解法步骤是
.
2.解方程
3.观察下列式子，请指出哪些是方程，哪些是一元一次方程？哪些是二元一次方程？
（5）2x+3=1
二、数学概念
1.
中含未知数的方程叫做分式方程.
2、阅读课本p149页内容，参考课本中例题解方程：
解：
三、例题讲解
1.解方程=
2.结合上面两题，归纳：解分式方程的一般步骤是：
（1）“化”.在方程两边同乘以最简公分母，化成
方程；
（2）“解”即解这个
方程；
（3）“检验”：即把
方程的根代入
。如果值
，就是原方程的根；如果值
，就是增根，应当
。
四、总结反思
说说你的收获.
2、你还有什么问题？
五、反馈练习
1、识别分式方程.
下列方程中，
(1)，
(2)，
(3)，
(4)，
(5)
分式方程有
;整式方程有
.
2、解分式方程.
（1）
（2）
课本150页练习题（1）（2）
六、能力提升
1．把分式方程化为整式方程，正确的是（
）
A．
B．
C．
D．
2.解下列方程：
（1）+1=
（2）=-2．
（3）
七、作业布置
15.3分式方程（2）
新授课
主备：任百菊
审核：
甄玉秋
时间
班级：
姓名：
学习目标：
1.掌握分式方程的解法，会熟练地解可化为一元一次方程的分式方程.
2.了解解分式方程时可能无解的原因,知道解分式方程须检验，并掌握
分式方程检验的方法.
学习重点和难点
重点：会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的解.
难点：理解解分式方程时可能无解的原因，记住解分式方程必须检验.
一、预习内容
1.找一找：我们已经学习了分式，你能找出下列各组分式的最简公分母吗？
（1）与
（2）与
（3）与
（4）与
2.背一背：什么是分式方程？解分式方程的基本思想是什么？
3.试一试：通过上节课的学习，尝试解下列分式方程，祝你成功！
（1）
（2）
二、数学概念：
1.说一说：有的分式方程去分母后所得整式方程的解就是原分式方程的解，而有的方程去分母后所得整式方程的解却不是原分式方程的解，你知道为什么吗？
2.阅读教材150页至151页，思考解分式方程一般需要经过哪几个步骤？
然后组内讨论、交流、归纳.
例题讲解（精讲）
例1解方程
（1）
（2）
例2已知关于x的分式方程＋3＝无解，求m的值？
总结反思
1.说说本节课你的收获；
2.你还有什么问题吗？
反馈练习：
1．下列说法中，错误的是
（
）
A．分式方程的解等于0，就说明这个分式方程无解.
B．解分式方程的基本思路是把分式方程转化为整式方程.
C．检验是解分式方程必不可少的步骤.
D．能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解.
2．解分式方程时，去分母后变形为（
）
A．2+（x+2）=3（x-1）
B．
2-x+2=3（x-1）
C．2-（x+2）=3（1-
x）
D．2-（x+2）=3（x-1）
3、下列分式方程中，一定有解的是（
）
A．
B．
C．
D．
4、方程的解是
．
5、若=2是关于的分式方程的解，则的值为
．
能力提升
1、当x=______时，分式的值与分式的值相等．
2、若代数式的值为零，则x=　　．
3、已知关于x的方程无解，试求的值．
4、已知关于
作业布置
15.3
分式方程（3）
新授课
主备：
宋洪艳
审核：甄玉秋
时间：
班级：
姓名：
学习目标：
会分析题意找出等量关系.
会列出可化为一元一次方程的分式方程解决实际问题.
3.经历探索应用分式方程解决实际问题的过程，掌握分析问题、解决问题的能力.
学习重点：如何结合实际分析问题，列出分式方程.
学习难点：分析过程，得到等量关系.
预习内容
下列关于x的方程①，②，③1，④中，是分式方程的是（填序号）
2、当时，关于的分式方程无解．
3、分式方程的解是（
）
A.
x=1
B.
x=－1
C.
x=2D.
x=－2
4、分式方程的解是（　　）
A.2
B.0
C.1
D.3
5、农机厂职工到距工厂15千米的某地检修农机，一部分人骑自行车先走半小时后，其余人乘汽车出发，结果他们同时到达，已知汽车速度为自行车速度的3倍，若设自行车的速度为x千米/时，则所列方程为
（　　）　
　　A．
B．
C．
D．
6、甲、乙两班学生参加植树造林，已知甲班每天比乙班多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，若设甲班每天植树x棵，则根据题意可列出的方程为_____________．
概念模型
1、由以上练习5有关行程问题的应用题，得到基本关系是：路程=_____________．
时间=_____________．速度=_____________．
2、由以上练习6有关工程问题的应用题，得到基本关系是：工作时间=_____________．
工作总量=_____________．工作效率=_____________．
三、例题讲解
例3．两个工程队共同参加一项筑路工程，甲队单独施工1个月完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成.哪个队的施工速度快？
分析:甲队1个月完成总工程的1/3,设乙队单独施工1个月能完成总工程的1/x，那么甲队半个月能完成总工程的_______．乙队半个月能完成总工程的_______．
两队半个月能完成总工程的_______．
列方程解决问题：
例4：某列列车平均提速v千米/时.用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度是多少？
分析：这里的v，s表示已知数据，设提速前列车的平均速度为x千米/时，那么提速前列车行驶s千米所用时间为_______h，提速后列车的平均速度为_______千米/时，提速后列车运行（s+50）千米所用时间为_______h.
列方程解决问题：
四、总结反思：
1、谈谈你的收获；
2、你还有什么问题？
五、反馈练习：
1.
一台电子收报机，它的译电效率相当于人工译电效率的75倍，译电3000个字比人工少用2小时28分，这台收报机与人工每分各译电__________字（　　）
　
A．78000，1200
B．12000，78000
　
C．97500，13000
D．90000，1200
2、某工地调来72人挖土和运土，已知3人挖出的土1人恰好能全部运走，怎样调配劳动力使挖出的土能及时运走且不窝土，解决此问题可设派x人挖土，其它人运土，列方程:
①x+3x=72，②72-x=，③，
④.上述所列方程正确的有(
)
A.1个
B.2个
C.3个
D.4个
3、“5·12”汶川大地震导致某铁路隧道被严重破坏．为抢修其中一段120米的铁路，施工队每天比原计划多修5米，结果提前4天开通了列车．问原计划每天修多少米？某原计划每天修米，所列方程正确的是（
）
A．
B．
C．
D．
4．某校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？设原价每瓶元，则可列出方程为（
）
A．
B．
C.
D．
5．甲、乙两人同时从A地出发，骑自行车行30千米到B地，甲比乙每小时少走3千米，结果乙先到40分钟.若设乙每小时走x千米，则可列方程（
）
A.
B.
C.
D.
能力提升
1.某林场原计划在一定期限内固沙造林240公顷，实际每天固沙造林的面积比原计划多4公顷，结果提前5天完成任务，设原计划每天固沙造林x公顷，根据题意列方程正确的是（
）.
（A）
（B）
（C）
（D）
2、某校师生到距学校20千米的公路旁植树，甲班师生骑自行车先走，45分钟后，乙班师生乘汽车出发，结果两班师生同时到达，已知汽车的速度是自行车速度的2.5倍，求两种车的速度各是多少
3、甲做90个机器零件所用的时间与乙做120个机器零件所用的时间相等，又已知平均每小时甲、乙两人一共做了35个零件，求甲、乙每小时各做多少个？
4.
若干人乘坐若干辆汽车..如果每辆汽车坐22人，有1人不能上车；如果有一辆车放空，那么所有旅客正好能平均分乘到其他各车上.已知每辆车最多能容纳32人，那么汽车数和旅客数各是多少？
5.甲、乙分别从相距36千米的A、B两地同时相向而行．甲从A出发到1千米时发现有东西遗忘在A地，立即返回，取过东西后又立即从A向B行进，这样二人恰好在AB中点处相遇，又知甲比乙每小时多走0.5千米，那么甲、乙的速度各是多少？
七、作业布置：教科书154页第3题、4题、5题
【归纳】
解分式方程的基本思想：
把分式方程“转化”为
，再利用
的解法求解。
解分式方程的方法：
在方程的两边同乘
，就可约去
，化成
。