24.1.4 圆周角 课件

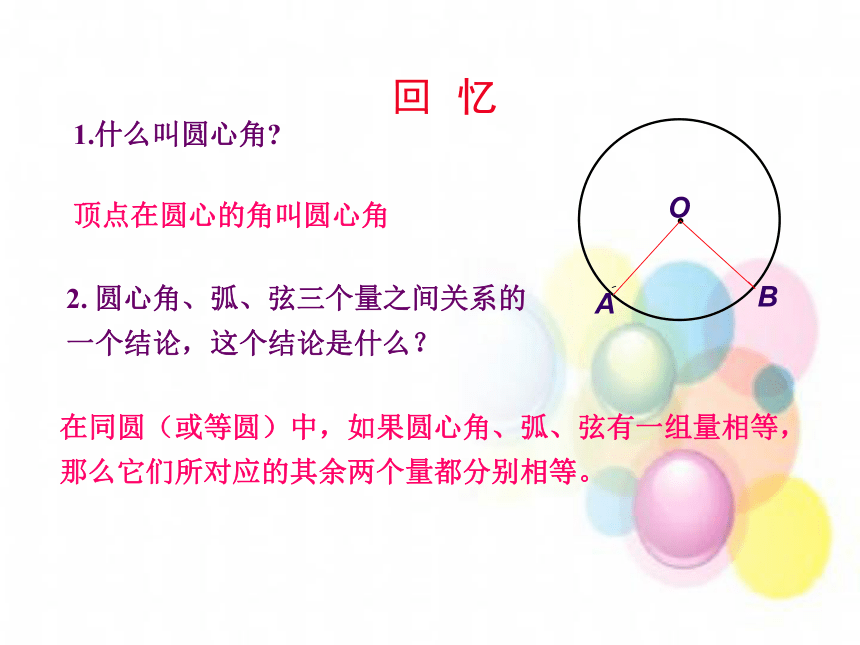
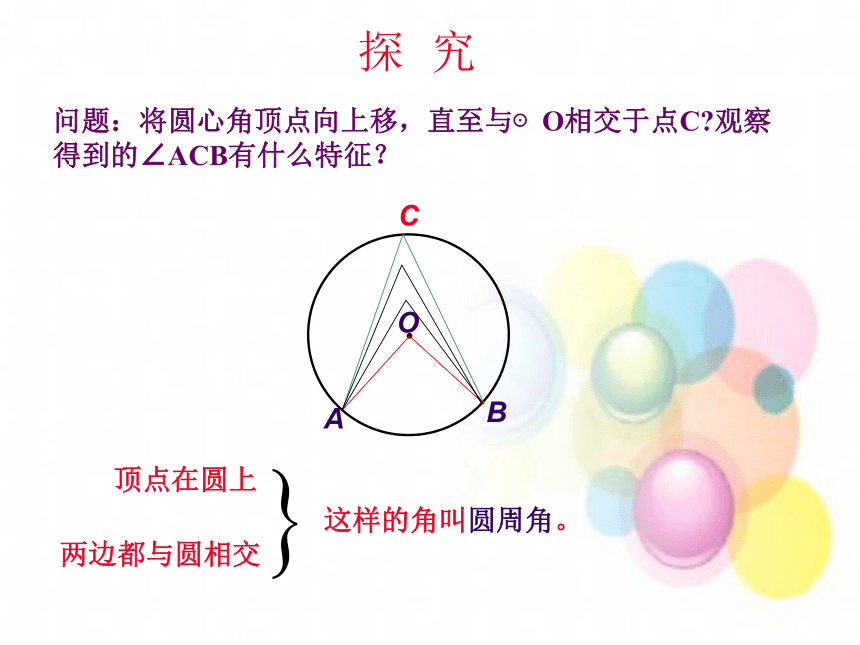
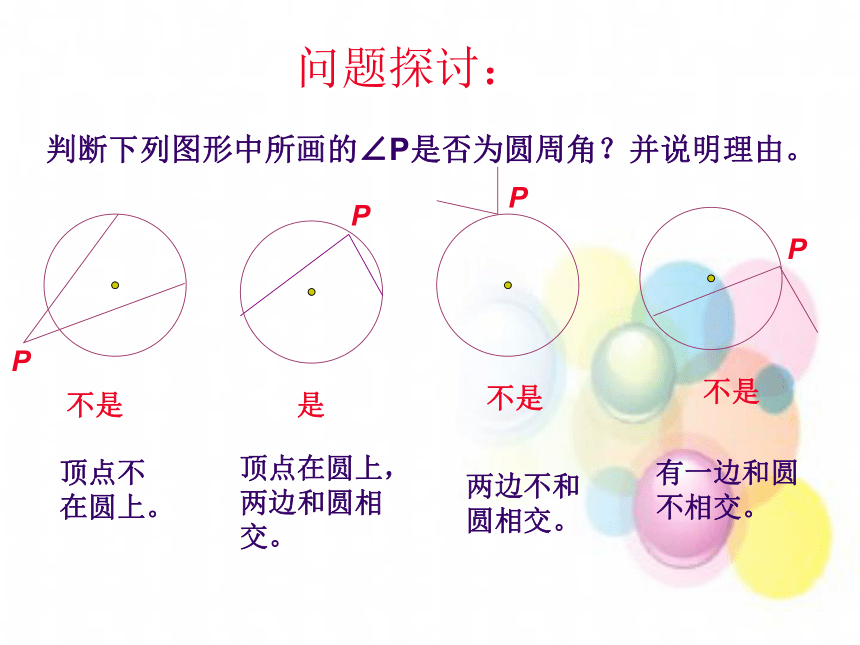
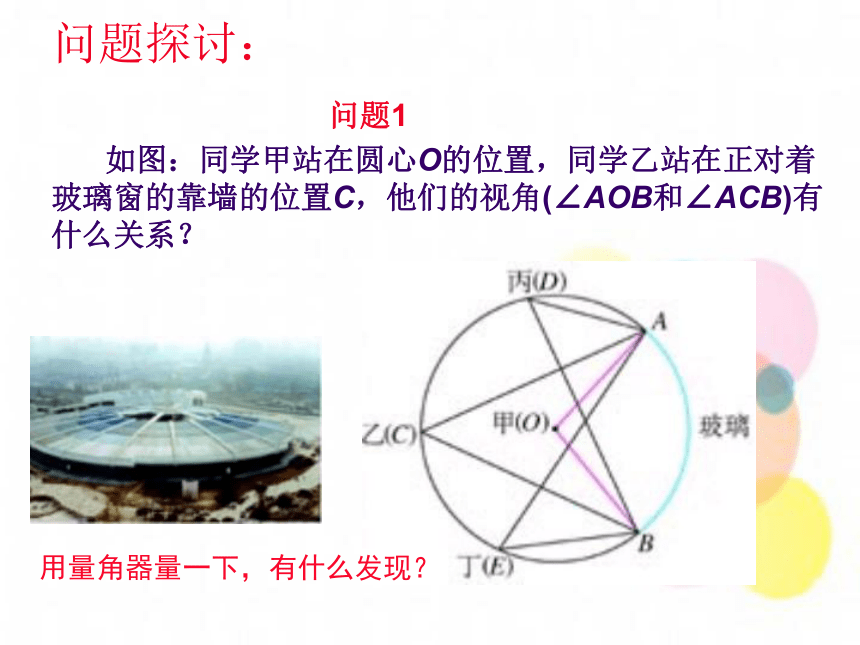
课件21张PPT。圆周角回 忆1.什么叫圆心角?顶点在圆心的角叫圆心角2. 圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？在同圆（或等圆）中，如果圆心角、弧、弦有一组量相等，那么它们所对应的其余两个量都分别相等。探 究OA问题：将圆心角顶点向上移，直至与⊙O相交于点C?观察得到的∠ACB有什么特征？C顶点在圆上两边都与圆相交这样的角叫圆周角。B问题探讨：判断下列图形中所画的∠P是否为圆周角？并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上，两边和圆相交。两边不和圆相交。有一边和圆不相交。观察思考： 在这个海洋馆里，人们可以通过其中的圆弧形玻璃窗观看窗内的海洋动物． 问题探讨： 问题1
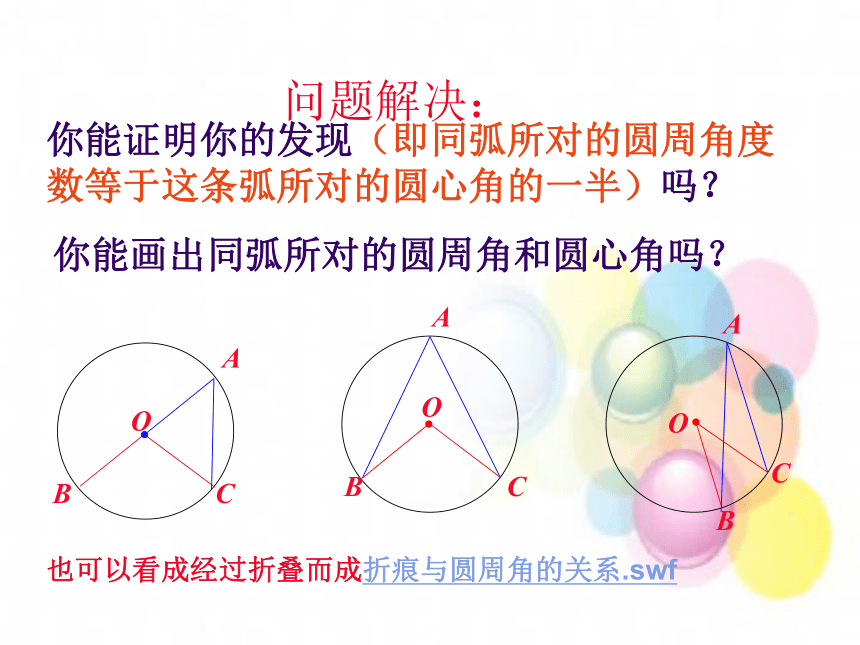
如图：同学甲站在圆心O的位置，同学乙站在正对着玻璃窗的靠墙的位置C，他们的视角(∠AOB和∠ACB)有什么关系？ 用量角器量一下，有什么发现？问题解决：你能画出同弧所对的圆周角和圆心角吗？你能证明你的发现（即同弧所对的圆周角度数等于这条弧所对的圆心角的一半）吗？也可以看成经过折叠而成折痕与圆周角的关系.swf分析论证1.首先考虑一种特殊情况：
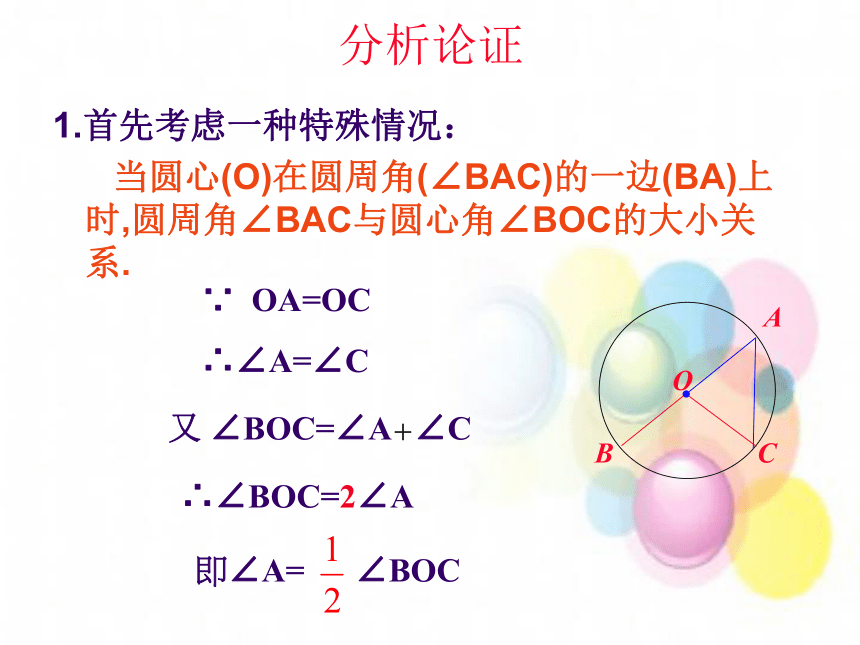
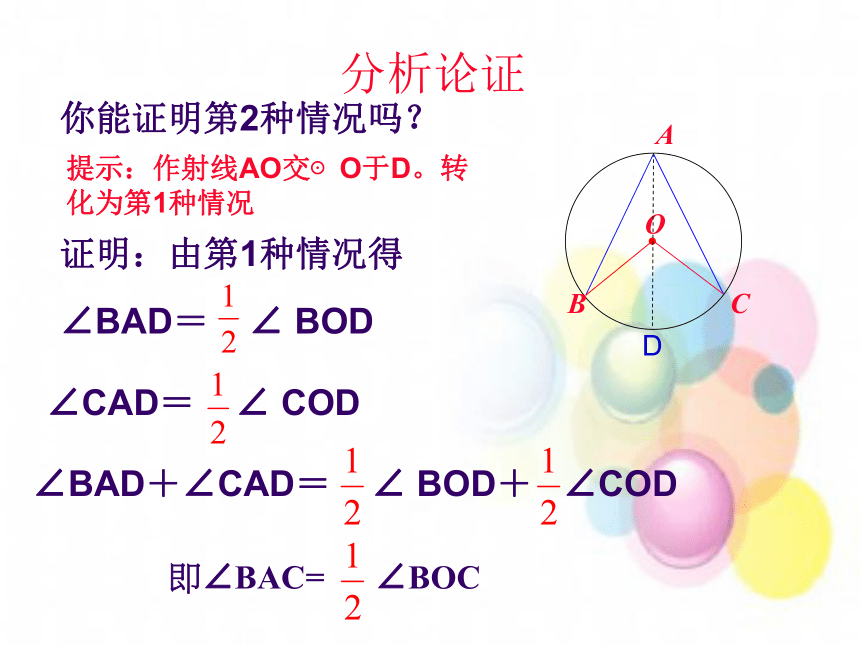
当圆心(O)在圆周角(∠BAC)的一边(BA)上时,圆周角∠BAC与圆心角∠BOC的大小关系.∵ OA=OC∴∠A=∠C又 ∠BOC=∠A＋∠C∴∠BOC=2∠A分析论证你能证明第2种情况吗？D提示：作射线AO交⊙O于D。转化为第1种情况证明：由第1种情况得 分析论证你能证明第3种情况吗？证明：作射线AO交⊙O于D。由第1种情况得 D问题解决：综上所述：我们得到：同弧所对的圆周角度数等于这条弧所对的圆心角的一半 问题２
如果同学丙、丁分别站在其他靠墙的位置
D和E，他们的视角(∠ADB和∠AEB)和同学乙的
视角相同吗？ 相等。都等于∠BOC的一半。圆周角定理： 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。推论：在同圆或等圆中，如果两个圆周角相等，那么它们所对的弧相等，所对的弦一定相等。思考：定理中的“同弧或等弧”能否改为“同弦或等弦”？练习： 如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？∠1＝∠4∠2＝∠7∠3＝∠6∠5＝∠8解： 问题1：如图，AB是⊙O的直径，请问：
∠C1、∠C2、∠C3的度数是 。 推论：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。 问题2： 若∠C1、∠C2、∠C3是直角，那么∠AOB是 。90°180°探究与思考：内接多边形如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆. 如图：四边形ABCD是⊙O的内接四边形，⊙O是四边形ABCD的外接圆.利用圆周角定理：我们可得
圆内接四边形的对角互补。在同圆中，同弦所对的圆周角互补练一练1、如图，在⊙O中，∠ABC=50°，
则∠AOC等于（ ）
A、50°； B、80°；
C、90°； D、100°D2、如图，△ABC是等边三角形，
动点P在圆周的劣弧AB上，且不
与A、B重合，则∠BPC等于（ ）
A、30°； B、60°；
C、90°； D、45°B练一练3、如图，∠A=50°， ∠ABC=60 °
BD是⊙O的直径，则∠AEB等于（ ）
A、70°； B、110°；
C、90°； D、120°B4、如图，△ABC的顶点A、B、C
都在⊙O上，∠C＝30 °，AB＝2，
则⊙O的半径是 。解：连接OA、OB∵∠C=30 ° ，∴∠AOB=60 °又∵OA=OB ，∴△AOB是等边三角形∴OA=OB=AB=2，即半径为2。2练一练5、如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC交⊙O于点F，点F不与点A重合。
（1）AB与AC的大小有什么关系？为什么？
（2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由。∴△ABC是锐角三角形解：（1）AB=AC。证明：连接AD又∵DC=BD，∴AB=AC。（2）△ABC是锐角三角形。由（1）知，∠B=∠C＜90 °连接BF，则∠AFB=90 °，∴∠A＜90 °∵AB是直径，∴∠ADB=90°，6. 如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长.7. 求证，如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形。再见！