1. 2一定是直角三角形吗 教学详案
文档属性
| 名称 | 1. 2一定是直角三角形吗 教学详案 |  | |
| 格式 | zip | ||
| 文件大小 | 409.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-22 05:29:27 | ||
图片预览




文档简介
2 一定是直角三角形吗
1.经历勾股定理的逆定理的探索过程,进一步发展推理能力.
2.掌握勾股定理的逆定理及勾股数的概念,并能进行简单的应用.
进一步发展数感,增加对勾股数的直观体验,培养从实际问题抽象出数学问题的能力,建立数学模型.
1.通过介绍有关历史资料,激起学生的学习兴趣和解决问题的欲望.
2.通过对勾股定理逆定理的综合应用,培养学生学习数学的兴趣及克服困难的勇气,体验勾股定理及其逆定理在实际生活中的实用性.
【重点】 运用身边熟悉的事物,从多种角度发展数感,会通过边长判断一个三角形是不是直角三角形,并会辨析哪些问题应用哪个结论.
【难点】 会辨析哪些问题应用哪些结论.
【教师准备】 教材P9图1 - 9,1 - 10的投影图片.
【学生准备】 复习勾股定理及其证明.
导入一:
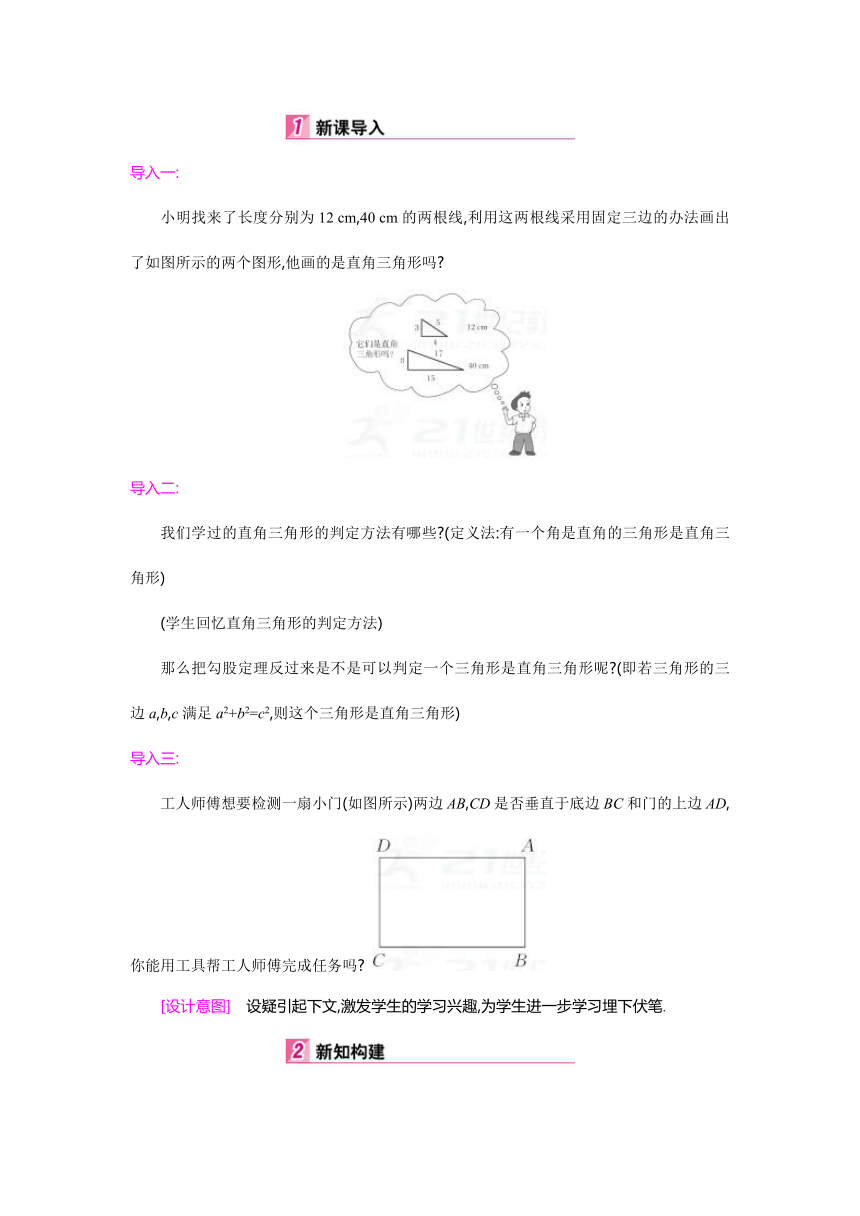
小明找来了长度分别为12 cm,40 cm的两根线,利用这两根线采用固定三边的办法画出了如图所示的两个图形,他画的是直角三角形吗?
导入二:
我们学过的直角三角形的判定方法有哪些?(定义法:有一个角是直角的三角形是直角三角形)
(学生回忆直角三角形的判定方法)
那么把勾股定理反过来是不是可以判定一个三角形是直角三角形呢?(即若三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形)
导入三:
工人师傅想要检测一扇小门(如图所示)两边AB,CD是否垂直于底边BC和门的上边AD,你能用工具帮工人师傅完成任务吗?
[设计意图] 设疑引起下文,激发学生的学习兴趣,为学生进一步学习埋下伏笔.
[过渡语] 如果一个三角形的三边长分别是3,4,5,那么这个三角形是直角三角形吗?
一、探究活动:一定是直角三角形吗
(1)分别以5,12,13;3,4,5;8,15,17;7,24,25为三边长作三角形,用量角器量一量,它们都是直角三角形吗?
(学生分工合作,可以每人选一组数作三角形)
(2)如果每组数中三边的长度分别是a,b,c,那么它们满足a2+b2=c2吗?
(学生回答,可能有学生会给出“反证法”的理由)
(3)根据(1)(2)你能总结出怎样的结论?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
(4)勾股定理和其逆定理有什么区别?
(5)给出勾股数的定义(满足a2+b2=c2的三个正整数,称为勾股数),并强调注意事项:
①符合a2+b2=c2;
②必须是正整数.
(学生举出常见的勾股数,注意教师强调的内容)
二、例题讲解
一个零件的形状如下图(左)所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如下图(右)所示,这个零件符合要求吗?
〔解析〕 如果三角形三边之间的关系存在着a2+b2=c2,那么就可以判定是直角三角形.
解:在ΔABD中,AB2+AD2=9+16=25=BD2,所以ΔABD是直角三角形,∠A是直角.
在ΔBCD中,BD2+BC2=25+144=169=CD2,所以ΔBCD是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
【思考】 在上面的零件中,如果有一个角是直角,这个零件算是合格的吗?
[知识拓展] 1.勾股定理与其逆定理的关系:勾股定理是已知直角三角形,得到三边长的关系,它是直角三角形的重要性质之一;而勾股定理的逆定理是由三角形三边长的关系判断一个三角形是不是直角三角形,这是直角三角形的判定,也是判断两直线是否垂直的方法之一.二者的条件和结论刚好相反.
2.勾股定理的逆定理的延伸:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形;如果a2+b2
3.勾股定理的逆定理的应用:应用勾股定理的逆定理可以判断一个三角形是不是直角三角形,在实际应用时,可用较短两边长的平方和与较长边长的平方作比较,若它们正好相等,则三角形为直角三角形,较长边所对的角为直角.
1.勾股定理的逆定理:如果三角形的三边长a,b,c满足:a2+b2=c2,那么这个三角形是直角三角形.
2.该逆定理是判定一个三角形是不是直角三角形的判定方法.
1.以以下各组数为三边长的三角形中,能组成直角三角形的是 ( )
A.3,4,6 B.9,12,15
C.5,12,14 D.10,16,25
解析:A.32+42≠62,故不是直角三角形,故不正确;B.92+122=152,故是直角三角形,故正确;C.52+122≠142,故不是直角三角形,故不正确;D.102+162≠252,故不是直角三角形,故不正确.故选B.
2.ΔABC的三边长分别为a,b,c,在下列条件下,不能判定ΔABC是直角三角形的是 ( )
A.a2=b2-c2
B.a2∶b2∶c2=1∶2∶3
C.∠A=∠B-∠C
D.∠A∶∠B∶∠C=3∶4∶5
解析:A.∵a2=b2-c2,∴a2+c2=b2,故本选项正确;B.∵a2∶b2∶c2=1∶2∶3,∴令a2=x,则b2=2x,c2=3x,∵x+2x=3x,∴a2+b2=c2,故本选项正确;C.∵∠A=∠B-∠C,∴∠B=∠A+∠C,∵在ΔABC中,∠A+∠B+∠C=180°,∴2∠B=180°,即∠B=90°,故本选项正确;D.∵∠A∶∠B∶∠C=3∶4∶5,∴设∠A=3x,则∠B=4x,∠C=5x,∵∠A+∠B+∠C=180°,即3x+4x+5x=180°,解得x=15°,∴5x=5×15°=75°<90°,故本选项错误.故选D.
3.如图所示,四边形ABCD中,AB=3,BC=4,AC=5,CD=12,AD=13,则四边形ABCD的面积为 ( )
A.72 B.36 C.66 D.42
解析:∵AB2+BC2=32+42=25=52=AC2,∴ΔABC是直角三角形. AC2+CD2=52+122=132=AD2,∴ΔACD是直角三角形,∴S四边形ABCD=AB·BC+AC·CD=×3×4+×5×12=36.故选B.
4.如图所示,在ΔABC中,AB=26,BC=20,边BC上的中线AD=24.求AC.
解:在ΔABD中,∵AB=26,AD=24,BD=CD=BC=10,∴满足AB2=AD2+BD2,∴ΔABD为直角三角形,即AD⊥BC.又∵BD=DC,即D为BC的中点,∴ΔABC为等腰三角形,即AC=AB=26.故AC的长为26.
2 一定是直角三角形吗
1.勾股定理的逆定理.
2.例题讲解.
一、教材作业
【必做题】
教材第10页随堂练习第1,2题.
【选做题】
教材第10页习题1.3第3题.
二、课后作业
【基础巩固】
1.下列几组数中,是勾股数的是 ( )
A.5,6,7 B.3,4,9
C.5,3,6 D.10,24,26
2.有五根木棒,它们的长度分别为2 cm,6 cm,8 cm,10 cm,12 cm,从中取出三根首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为 ( )
A.2 cm,6 cm,8 cm B.6 cm,8 cm,10 cm
C.6 cm,8 cm,12 cm D.2 cm,8 cm,10 cm
3.如图所示,有一块地,已知AD=4 m,CD=3 m,∠ADC=90°,AB=13 m,BC=12 m,则这块地的面积为 ( )
A.24 m2 B.26 m2
C.28 m2 D.30 m2
4.若ΔABC的三边长a,b,c满足|a-5|+(b-12)2+(c-13)2=0,则ΔABC的面积为 .?
【能力提升】
5.观察下列几组勾股数:①3,4,5;②5,12,13;③7,24,25;④9,40,41;⑤15,m,n.根据你发现的规律可得m+n= .?
6.如图所示,∠C=90°,AC=12,BC=9,AD=8,BD=17,求ΔABD的面积.
7.已知a,b,c为ΔABC的三边长,且满足a2c2-b2c2=a4-b4,试判断ΔABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2).②
∴c2=a2+b2.③
∴ΔABC是直角三角形.
(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ;?
(2)错误的原因为 ;?
(3)写出本题正确的解题过程.
8.求证若勾股数组中,弦与股的差为1.证明这样的勾股数组可表示为如下形式:2a+1,2a2+2a,2a2+2a+1,其中a为正整数.
9.国道通过A,B两村庄,而C村庄离国道较远,为了响应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道.已知C村到A,B两村的距离分别为6 km,8 km,A,B两村距离为10 km,那么这条水泥路的最短距离为多少?
【拓展探究】
10.已知某直角三角形的两直角边长分别是a,b,斜边长为c,那么三边长分别为a+1,b+1,c+1的三角形会不会是直角三角形呢?请说明理由(提示:若a+b>c,则a+b-c>0).
【答案与解析】
1.D(解析:A.52+62≠72,不能构成直角三角形,故不是勾股数;B.32+42≠92,不能构成直角三角形,故不是勾股数;C.32+52≠62,不能构成直角三角形,故不是勾股数;D.102+242=262,能构成直角三角形,是正整数,故是勾股数.故选D.)
2.B(解析:∵62+82=102,∴长度分别为6 cm,8 cm,10 cm的三根木棒首尾顺次连接可搭成一个直角三角形.故选B.)
3.A(解析:如图所示,连接AC.由勾股定理可知,AC2=32+42=25=52,AC=5,又∵AC2+BC2=52+122=132=AB2,∴ΔABC是直角三角形,故所求面积=ΔABC的面积-ΔACD的面积=×5×12-×3×4=24(m2).故选A.)
4.30(解析:∵|a-5|+(b-12)2+(c-13)2=0,∴a-5=0,b-12=0,c-13=0,解得a=5,b=12,c=13,∵52+122=132,∴ΔABC是直角三角形,∴ΔABC的面积为5×12÷2=30.故答案为30.)
5.225(解析:由题意得第n组数为2n+1,,,∴第1个数为15时,即相当于第7组数据,∴m==112,n==113,∴m+n=112+113=225,故答案为225.)
6.解:∵∠C=90°,AC=12,BC=9,∴AB2=AC2+CB2,∴AB=15.∵AD=8,BD=17,∴DB2=AD2+AB2,∴∠DAB=90°,∴ΔABD的面积=AB×AD=60.故ΔABD的面积为60.
7.解:(1)③ (2)除式可能为零 (3)∵a2c2-b2c2=a4-b4,∴c2(a2-b2)=(a2+b2)(a2-b2).∴a2-b2=0或c2=a2+b2.当a2-b2=0时,a=b;当c2=a2+b2时,∠C=90°.∴ΔABC是等腰三角形或直角三角形.
8.证明:设勾长为x,弦长为z,则股长为z-1,∴x,z-1,z是一个基本勾股数组.若z为奇数,则z-1为偶数,若z为偶数,则z-1是奇数,∴x为奇数,
设x=2a+1(a为正整数),则有(2a+1)2+(z-1)2=z2,解得z=2a2+2a+1,故勾股数组具有形式2a+1,2a2+2a,2a2+2a+1.
9.解:如图所示,过点C作CD⊥AB于D,则这条水泥路的最短距离为CD的长度.∵BC2+AC2=82+62=100,AB2=102=100,∴BC2+AC2=AB2,∴∠ACB=90°.∵SΔABC=AB·CD=AC·BC,∴CD==4.8(km).故这条水泥路的最短距离为4.8 km.
10.解:∵某直角三角形的两直角边长分别是a,b,斜边长为c,∴a2+b2=c2,∵(a+1)2+(b+1)2=a2+2a+1+b2+2b+1,(c+1)2=c2+2c+1,∴(a+1)2+(b+1)2-(c+1)2=2a+2b-2c+1,∵a+b>c,∴a+b-c>0,∴(a+1)2+(b+1)2-(c+1)2>1≠0,∴三边长分别为a+1,b+1,c+1的三角形不是直角三角形.
充分尊重教材,以勾股定理的逆向思维模式引入“如果一个三角形的三边长a,b,c满足a2+b2=c2,是否能得到这个三角形是直角三角形”的问题,充分引用教材中出现的例题和练习.
未能注重并及时引导学生积极参与实验活动,没有完全让学生从中体验:任何一个数学结论的发现总是要经历观察、归纳、猜想和验证的过程,这使得学生的认知不能很好地遵循由“特殊→一般→特殊”的发展规律.
在充分备课的基础上,要特别注意学生的实际情况与认知能力,及时地引导学生参与实验活动,从而让学生在亲身参与过程中体验数学结论所经历的观察、归纳、猜想和验证等过程.在利用今天所学知识解决实际问题时,引导学生善于对公式变形,便于简便计算.加强对学习新知识理解较困难的学生的关注.
随堂练习(教材第10页)
1.解:(1)因为92+122=152,所以9,12,15能作为直角三角形的三边长. (2)因为122+182≠222,所以12,18,22不能作为直角三角形的三边长. (3)因为122+352≠362,所以12,35,36不能作为直角三角形的三边长. (4)因为152+362=392,所以15,36,39能作为直角三角形的三边长.
2.解:因为AB=4,AE=2,DF=1,所以ED=2,FC=3,BC=4,所以BE2=AB2+AE2=20,EF2=ED2+DF2=4+1=5,BF2=BC2+CF2=16+9=25,所以BE2+EF2=BF2,所以ΔBEF是直角三角形.所以图中共有4个直角三角形,它们是ΔABE,ΔBCF,ΔDEF和ΔBEF.
习题1.3(教材第10页)
1.解:斜边的平方=92+402=1681=412,所以斜边长为41.
2.解:是,因为通过移项可以得到a2+b2=c2.
3.解:(1)还是直角三角形. (2)填表(从左至右,从上至下):9,12,15 12,16,20 30,40,50 10,24,26 20,48,52 50,120,130 16,30,34 24,45,51 80,150,170 14,48,50 21,72,75 28,96,100 这些勾股数的任意倍都是勾股数,理由如下:设a,b,c是一组勾股数,且a2+b2=c2,将a,b,c同时扩大为原来的k倍(k为正整数),得ka,kb,kc,因为(ka)2+(kb)2=k2a2+k2b2=k2(a2+b2)=k2c2,所以ka,kb,kc是勾股数.
4.解:如图所示,④和⑤是直角三角形,其余三角形不是直角三角形.设每个小方格的边长为1,则A1=9,B1=5,A1=8,而5+8≠9,故ΔA1B1C1不是直角三角形.A2=25,B2=10,A2=9,而9+10≠25,故ΔA2B2C2不是直角三角形.A3=17,B3=10,A3=5,而5+10≠17,故ΔA3B3C3不是直角三角形.A4=20,B4=10,A4=10,10+10=20,故ΔA4B4C4是直角三角形.A5=26,A5=13,B5=13,13+13=26,故ΔA5B5C5是直角三角形.A6=13,B6=10,A6=17,而10+13≠17,故ΔA6B6C6不是直角三角形.
5.解:方法不唯一,如:可以取任意长的一段(可以打结标记),然后对折取出等长的12段,分别取3段,4段和5段作为三角形的三边长,所得到的三角形就是直角三角形.
判定一个三角形是不是直角三角形有两种方法:
(1)利用定义,如果已知条件与角度有关,可借助三角形内角和求出其中一个角是直角,判定是直角三角形;
(2)利用勾股定理的逆定理,利用这一方法的题目,一般是给定或者可通过计算推导出三角形三边的数量关系:a2+b2=c2.
直角三角形——
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
