1.3勾股定理的应用 教学详案

3　勾股定理的应用
1.能正确运用勾股定理及直角三角形的判别方法解决简单的实际问题.
2.学会选择适当的数学模型解决实际问题,进一步发展应用意识.
通过问题情境的设立,使学生体会数学来源于生活,又应用于生活;积累利用数学知识解决日常生活中实际问题的经验和方法.
敢于面对数学学习中的困难,增加遇到困难时
选择其他方法的经验,进一步体会数学的应用价值,发展运用数学的信心和能力,初步形成积极参与数学活动的意识.
【重点】　能运用勾股定理及直角三角形的判别方法解决实际问题.
【难点】　正确选择勾股定理及直角三角形的判别方法解决实际问题.
【教师准备】　教材例题图片.
【学生准备】　复习勾股定理及其逆定理.
导入一:
折竹抵地(源自《九章算术》):今有竹高一丈,风折抵地,去本三尺.问折者高几何?
大意:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处距离原竹子底部3尺远.问原来的竹子有多高?
导入二:
历史上伦敦克里斯蒂拍卖行贴出了如下的一个土地拍卖广告:如图所示,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩,116英亩,370英亩.三个正方形恰好围着一个池塘,若有人能计算出池塘的准确面积,则池塘不计入土地价钱白白奉送.英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗?
　　[过渡语]　接下来我们体验一下勾股定理的应用.
一、问题探究
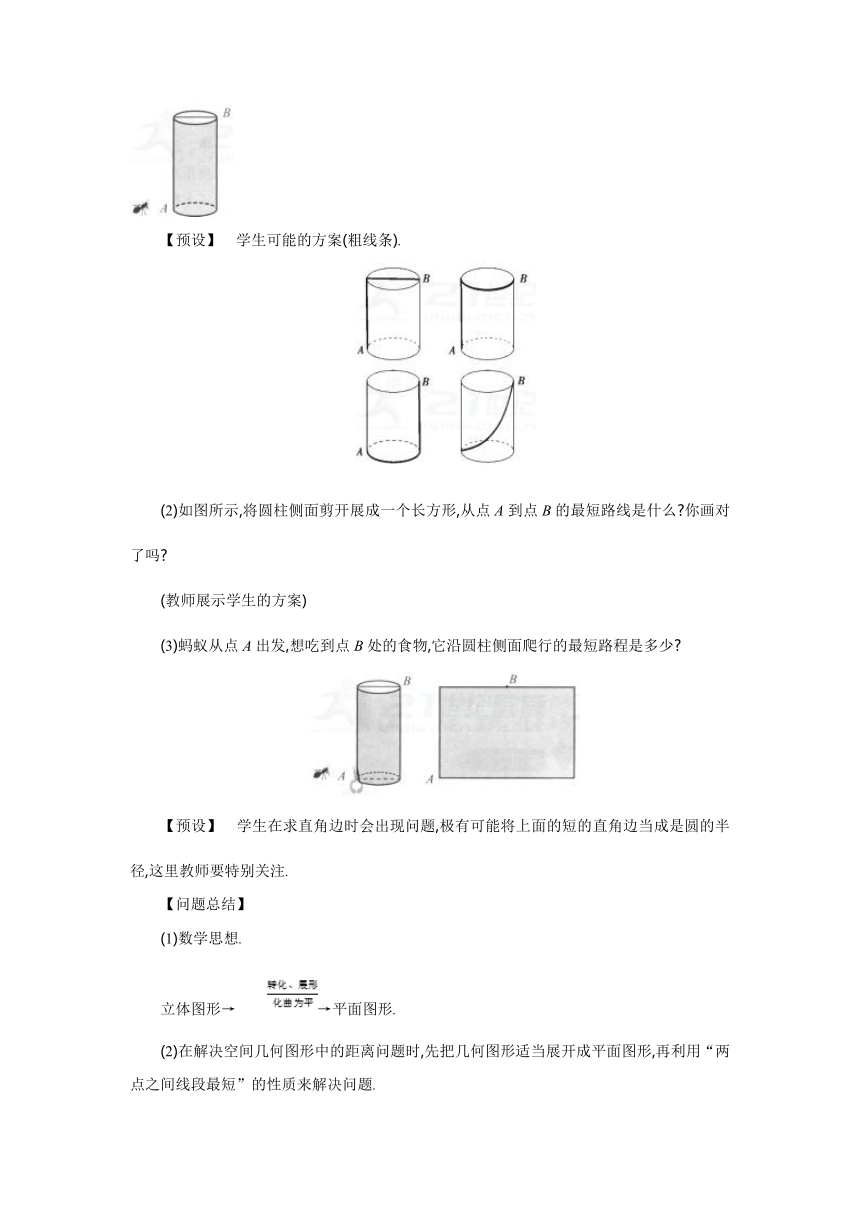
如图所示,有一个圆柱,它的高等于12 cm,底面上圆的周长等于18 cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的
食物,沿圆柱侧面爬行的最短路程是多少?
思路一
(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条路线,你觉得哪条路线最短呢?
【预设】　学生可能的方案(粗线条).
(2)如图所示,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么?你画对了吗?
(教师展示学生的方案)
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
【预设】　学生在求直角边时会出现问题,极有可能将上面的短的直角边当成是圆的半径,这里教师要特别关注.
【问题总结】
(1)数学思想.
立体图形→→平面图形.
(2)在解决空间几何图形中的距离问题时,先把几何图形适当展开成平面图形,再利用“两点之间线段最短”的性质来解决问题.
[设计意图]　通过对上述问题的探索,渗透建模思想,通过探求过程,学生学会分析立体图形中隐藏的平面模型(直角三角形),能够将立体图形转化为平面图形,体会勾股定理在生活中是广泛存在的,激发和点燃学生学习的兴趣,为后续学习起到引领和铺设作用.
思路二
教师展示教材上本节开头问题,学生思考,少数学生能得到正确答案.(学生课下已仿照图1 - 11作了一个圆柱体)按老师的要求去做.
下面我们动手操作一下,看看为什么这是最短路线.
(1)按题目要求在圆柱上画出A,B两点.
(2)从A点到B点沿圆柱侧面画出几条路线.
(3)将圆柱侧面从A点剪开展成一个长方形.
(教师巡视指导,避免学生操作错误)
(学生解释为什么这就是最短路线.动手剪成长方形,铺平)
【教师提问】　在同学们剪成的长方形所画的路线中,你能替蚂蚁找到最短的路线吗?能用我们所学过的知识对最短路线做出解释吗?
(学生思考、观察并找到最短的路线,并求出最短路程,小组讨论)
教师用多媒体出示教材上的“做一做”,并提出问题.
李叔叔想要检测雕塑(如图所示)底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30 cm,边AB长是40 cm,点B,D之间的距离是50 cm,边AD垂直于边AB吗?
(3)小明随身只有一个长度为20 cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
对学生完成情况作出判断,对有创新精神的同学予以表扬.
二、例题讲解
教师出示例题.
　如图所示的是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3 m,CD=1 m,试求滑道AC的长.
解:设滑道AC的长度为x m,则AB的长度为x m,AE的长度为(x-1) m.
在RtΔACE中,∠AEC=90°,由勾股定理得AE2+CE2=AC2,即(x-1)2+32=x2,解得x=5.
故滑道AC的长度为5 m.
[知识拓展]　1.解决两点距离问题:正确画出图形,已知直角三角形两边长,利用勾股定理求第三边长.
2.解决航海问题:理解方向角等概念,根据题意画出图形,利用勾股定理或其逆定理解题.
3.解决实际问题中两线段是否垂直的问题:以已知两线段为边构造一个三角形,根据三边的长度,利用勾股定理的逆定理解题.
4.解决折叠问题:正确画出折叠前、后的图形,运用勾股定理及方程思想解题.
5.解决梯子问题:梯子架到墙上,梯子、墙、地面可构成直角三角形,利用勾股定理等知识解题.
6.解决侧面展开问题:将立体图形的侧面展开成平面图形,利用勾股定理解决表面距离最短的问题.
1.当已知条件告诉了有直角三角形时,直接用勾股定理解决问题;当已知条件告诉了边长之间的关系时,可想到用勾股定理的逆定理先证明是直角三角形.
2.当遇到曲面上两点的距离问题时,应想到化曲面为平面.
1.如图所示,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m.一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 (　　)
A.8 m　　　　　　B.10 m
C.12 m D.14 m
解析:如图所示,设大树高为AB=10 m,小树高为CD=4 m,过C点作CE⊥AB于E,则四边形EBDC是矩形,连接AC,∴EB=4 m,EC=8 m,AE=AB-EB=10-4=6(m),在RtΔAEC中,AC2=AE2+CE2=62+82=102,∴AC=10 m.故选B.
2.如图所示,将一根长24 cm的筷子放入底面直径为5 cm,高为12 cm的圆柱形水杯中,设筷子露在杯子外面的长度为h cm,则h的最小值是 (　　)
A.12 cm B.13 cm
C.11 cm D.9 cm
解析:如图所示,设杯子的底面直径为a,高为b,筷子在杯中的长度为c,根据勾股定理,得c2=a2+b2,∴c2=a2+b2=52+122=132,∴c=13 cm,∴h=24-13=11(cm).故选C.
3.某楼梯的侧面视图如图所示,其中AB=6.5米,BC=2.5米,∠C=90°,楼梯的宽度为6米,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的面积应为　　　　.?
解析:∵AB=6.5米,BC=2.5米,∠C=90°,∴AC2=AB2-BC2=62,∴AC=6米,∴地毯的长度为AC+BC=6+2.5=8.5(米),∴地毯的面积为8.5×6=51(平方米).故填51平方米.
4.如图所示,铁路AB的一边有C,D两村庄,DA⊥AB于A,CB⊥AB于B,已知AB=25 km,DA=15 km,CB=10 km,现要在铁路上建一个农产品收购站E,并使DE=CE,则农产品收购站E应建在距点A多少千米处?
解:设AE=x km,则BE=(25-x)千米,
∵C,D两村到E站的距离相等,
∴DE=CE,即DE2=CE2.
∵在RtΔDAE中,DA2+AE2=DE2,
在RtΔEBC中,BE2+BC2=CE2,
∴DA2+AE2=BE2+BC2,
即152+x2=102+(25-x)2,解得x=10.
故收购站E应建在距点A 10 km处.
3　勾股定理的应用
1.问题探究.
2.例题讲解.
一、教材作业
【必做题】
教材第14页随堂练习.
【选做题】
教材第14页习题1.4第3题.
二、课后作业
【基础巩固】
1.如图所示,一根竹子高9尺,折断后竹子顶端落在离竹子底端3尺处,折断处离地面高度是 (　　)
A.3尺　　　B.4尺　　　C.5尺　　　D.6尺
2.如图所示,一只蚂蚁从正方体的底面A点处沿着表面爬行到正方体上底面的B点处,它爬行的最短路线是 (　　)
A.A?P?B B.A?Q?B
C.A?R?B D.A?S?B
3.如图所示,一个圆柱的底面半径为8 cm,高为15π cm,一只蚂蚁从A点爬到B点的最短路程是　　　　cm.?
4.有一块边长为24米的正方形绿地ABCD(如图所示),在绿地的BC边上距B点7米的点E处有一健身器,居住在A处的居民经常践踏绿地,沿直线AE直达E处健身,小明同学想在A处立一块标牌“少走■米,踏之何忍?”,则标牌上的“■”处的数字是　　　　.?
5.如图所示,要从电线杆离地面12米处向地面拉一条长为13米的钢缆,求地面钢缆固定点A到电线杆底部B的距离.
【能力提升】
6.两艘轮船从同一港口同时出发,甲船时速40海里,乙船时速30海里,两小时后,两船相距100海里,已知甲船的航向为北偏东46°,则乙船的航向为 (　　)
A.东偏南46°
B.北偏西46°
C.东偏南46°或西偏北46°
D.无法确定
7.如图所示,已知长方体的三条棱AB,BC,BD的长分别为4,5,2,蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的平方是　　　　.?
8.一艘轮船以24海里/时的速度离开港口向东南方向航行,另一艘轮船同时以10海里/时的速度离开港口向西南方向航行,经过1小时,这两艘轮船相距多远?
9.如图所示,在长15米,宽8米的长方形ABCD花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点几米处?
10.如图所示,有一圆柱形油罐,要从A点环绕油罐搭梯子,正好到A点的正上方B点.梯子最短需要多少米?(已知油罐底面的周长是12 m,高AB是5 m)
【拓展探究】
11.如图所示,三条公路的交叉地带是一个三角形,经测量这个三角形的三条边长分别是AB=130米,BC=140米,AC=150米.市政府准备将其作为绿化用地,请你求出绿化用地的面积.
【答案与解析】
1.B(解析:设竹子折断处离地面x尺,则斜边为(9-x)尺,根据勾股定理,得x2+32=(9-x)2,解得x=4.故选B.)
2.A(解析:根据两点之间线段最短可知.故选A.)
3.17π(解析:展开图如图所示,CD的长为2π·8=16π.B为CD的中点,所以CB=8π,又AC=15π,AB2=(8π)2+(15π)2=(17π)2,所以AB=17π.一只蚂蚁从A点爬到B点的最短路程是17π cm.故答案为17π.)
4.6(解析:因为是一块正方形的绿地,所以∠B=90°,由勾股定理,得AE=25米,计算由A点顺着AB,BE到E点的路程是24+7=31(米),而AE=25米,则少走31-25=6(米).故答案为6.)
5.解:由题意得AC=13米,BC=12米,∠B=90°,AB2=AC2-BC2=52,故地面钢缆固定点A到电线杆底部B的距离为5米.
6.C(解析:根据题意,OA=40×2=80(海里),OB=30×2=60(海里),又因为AB=100海里,802+602=1002,所以OB2+OA2=AB2,根据勾股定理的逆定理,得ΔAOB为直角三角形.同理,ΔAOC也为直角三角形.所以∠AOB=90°,又因为∠1=46°,所以∠2=180°-90°-46°=44°,∠3=90°-44°=46°,根据对顶角相等,得∠4=∠3=46°,则乙船的航向为东偏南46°或西偏北46°.故选C.)
7.61(解析:如图(1):AM2=AB2+BM2=16+(5+2)2=65.如图(2):AM2=AC2+CM2=92+4=85.如图(3):AM2=AD2+DM2=62+52=61.∴蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的平方是61.故答案为61.)
8.解:根据题意得OA=10×1=10(海里),OB=24×1=24(海里),ΔAOB是直角三角形,∴AB2=102+242=262,∴AB=26海里,∴经过1小时,这两艘轮船相距26海里.
9.解:由题意知EF=13米,EA=5米.在RtΔEAF中,由勾股定理,得AF2=EF2一EA2,即AF2=132-52=144=122,所以FB=15-12=3(米),即另一端出口F应选在AB边上距B点3米处.
10.解:如图所示.∵AC=12 m,BC=5 m,∴AB2=52+122=132,∴AB=13 m.答:梯子最短需要13 m.
11.解:如图所示,作BC边上的高AD,设BD=x米,则CD=(140-x)米,在RtΔABD中,由勾股定理,得AD2=AB2-BD2,在RtΔACD中,由勾股定理,得AD2=AC2-CD2,所以AB2-BD2=AC2-CD2,即1302-x2=1502-(140-x)2,解得x=50.所以AD2=AB2-BD2=1302-502=(130+50)(130-50)=180×80=1202,则AD=120(取正值).所以,所求的面积为BC·AD=×140×120=8400(平方米).
从实际生活中得出数学知识,再回到实际生活中加以运用是本节课的一个教学“亮点”.在本节课预习案中的梯子问题有着学生非常熟悉的生活背景,课上部分的蚂蚁吃芝麻以及课后的渡河要偏离目标点的情境,相对来说也是学生比较感兴趣的问题,以此引入、深入勾股定理的应用,使数学教学在生活情境中得以创新.
教学没有彻底放开,和新的课程理念的要求存在着差距.如教学设计中的问题都是教者提出的,学生的主动性没有充分调动起来.
在课堂中,让学生自己动手剪几个边长分别为3,4,5;6,8,10;5,12,13的直角三角形,然后用勾股定理验证,激发学生的学习兴趣,充分调动学生学习积极性,给学生留有思考和探索的余地,让学生能在独立思考与合作交流中解决学习中的问题.
随堂练习(教材第14页)
解:甲走了6×2=12(km),乙走了5×1=5(km),因为122+52=132,所以上午10:00,甲、乙二人相距13 km.
习题1.4(教材第14页)
1.解:因为82+152=172,所以阴影长方形的长为17 cm,所以S阴=17×3=51(cm2).
2.解:在图(1)中,因为152+202≠242,所以以15,20,24为三边长的三角形不是直角三角形.在图(3)中,因为72+202≠252,所以以7,20,25为三边长的三角形不是直角三角形.在图(2)中,因为72+242=252,152+202=252,所以此图中的两个三角形都是直角三角形,所以图(2)是正确的.
3.解:能.因为11.72+92=136.89+81=217.89,152=225,即11.72+92<152,所以一架长为15 m的云梯能到达墙的顶端.
4.提示:把正面和右面展开在一个平面上,连接AB,则得到一个两直角边长分别为16 cm和12 cm的直角三角形,其斜边长即是最短路线长,为20 cm.
5.解:设这个水池的深度为x尺,则芦苇的长为(x+1)尺,由题意得(x+1)2=x2+52,所以x=12,所以x+1=13.答:这个水池的深度为12尺,这根芦苇的长度为13尺.
6.提示:借助勾股定理测算旗杆的高度,需要构造一个与旗杆有关的直角三角形.具体方案可以类似教材第197页总复习的第26题.
复习题(教材第16页)
1.提示:由勾股定理分别求出AB,BC,CD的长,再相加,可得折线的长为28 cm.
2.解:(1)(4)能,(2)(3)不能.
3.解:1602+1202=2002,从而可知这时它离出发点200 km.
4.解:在RtΔABC中,∠B=90°,所以AC2=AB2+BC2,所以AC=5 cm.同理CF=13 cm.所以S正方形CDEF=CF2=132=169(cm2).
5.解:由勾股定理得2502-1502=2002,所以小明向正东方向走了200 m.
6.解:两直角边上的半圆面积之和等于斜边上的半圆面积.
7.解:两图面积相等,前者面积=4×ab+c2,后者面积=4×ab+a2+b2,所以c2=a2+b2.
8.解:这个三角形的三边长分别为3,4,5,是一组勾股数,所以这个三角形是直角三角形.
9.解:(1)如图所示,正方形ABDE即为所求,作RtΔACB,AC=2,BC=7,∠C=90°,则S正方形ABDE=AB2=AC2+BC2=22+72=53.　(2)可以利用5=22+12,10=32+12,13=22+32构造正方形,图略.
10.解:(1)图略.　(2)所有正方形的面积和为4 cm2.　(3)像一棵美丽的大树.　(4)如果最初的直角三角形是等腰直角三角形,“毕达哥拉斯树”将是轴对称图形.
11.解:(1)24 m.　(2)不是.设底部在水平方向上滑动了x m,则由勾股定理得202+(7+x)2=252,所以(7+x)2=225,所以7+x=±15,所以x=8或x=-22(舍去),所以底部在水平方向上滑动了8 m.
12.提示:将长方体的侧面沿过A点的侧棱展开(如图所示),则蚂蚁爬行的最短距离是路线AB的长度.根据勾股定理得AB2=152+202=625,所以AB=25.故需要爬行的最短距离是25 cm.
13.解:如图所示,依题意知A'B'=1.5 m,B'C'=1.5 m,CC'=2.2 m,在RtΔA'B'C'中,A'C'2=A'B'2+B'C'2,在RtΔA'C'C中,A'C2=A'C'2+CC'2,代入数值即可得A'C≈3.056 m.所以能放入电梯内的木条的最大长度约是3.056 m.估计装修工人买的木条至少是3.056 m.
14.解:(1)勾股数中一定有一个是偶数.理由如下:如果全部为奇数,a2+b2为偶数,而c2为奇数,两者不可能相等.　(2)略.
勾股定理的逆定理及其应用在近年各地中考中是热点问题,题型多样,填空题、选择题、解答题、综合题均有.随着课程改革的不断深入,一些探索性问题也已出现,尤其是与工农业生产以及实际生活紧密联系的应用题更值得我们关注,目的是要考查学生运用数学知识解决实际问题的能力.
　如图所示,圆柱形玻璃杯,高为12 cm,
底面周长为18 cm,在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为　　　　cm.?