第二十三章《旋转》导学案(无答案)
图片预览


文档简介
第二十三章《旋转》导学案
23.1 图形的旋转(1) 新授课
学习目标:
通过观察具体实例认识旋转,归纳旋转、旋转中心、旋转角和对应点的概念,
并应用它们解决一些实际问题.
2.探索旋转的性质,会画出旋转后的图形.
学习重点和难点
重点:旋转、对应点的有关概念及其应用.
难点:对旋转现象进行分析研究,旋转后的现象进行探索.
预习内容
钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、风车叶片在转动过程中,其形状、大小、位置是否发生变化呢?
钟表的指针在不停地转动,从3时到5时,时针旋转了多少度?
数学概念
1. 像这样,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的 ,点O叫做 ,转动的角叫做 .
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的 .
2. 自学并完成课本60页的探究,归纳旋转的性质:
(1)对应点到旋转中心的距离__________.
(2)对应点与旋转中心所连线段的夹角等于________ .
(3)旋转前、后的图形___________ .
例题讲解
例1: 如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是哪点?旋转方向是什么?旋转角度是多少?点B的对应点是什么?
例2: 如下图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
总结反思
说说你的收获;
你还有什么问题?
反馈练习
1.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片
2.下列现象中属于旋转的有____个.
地下水位逐年下降;传送带的移动;方向盘的转动;水龙头的转动;钟摆的运动;荡秋千运动.
3.如图,如果把钟表的指针看成四边形AOBC,它绕着O点旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是____,旋转角是_________,经过旋转,点A转到___,点C转到___,点B转到___,线段OA、OB、BC、AC分别转到_____________________,∠A、∠B、∠C分别与___________________是对应角.
如图,将△ABC绕点A逆时针旋转80°得到△AB′C′.
若∠BAC=50°,则∠CAB′的度数为(?? )
A. 30°??? B. 40° C. 50°??? D. 80°
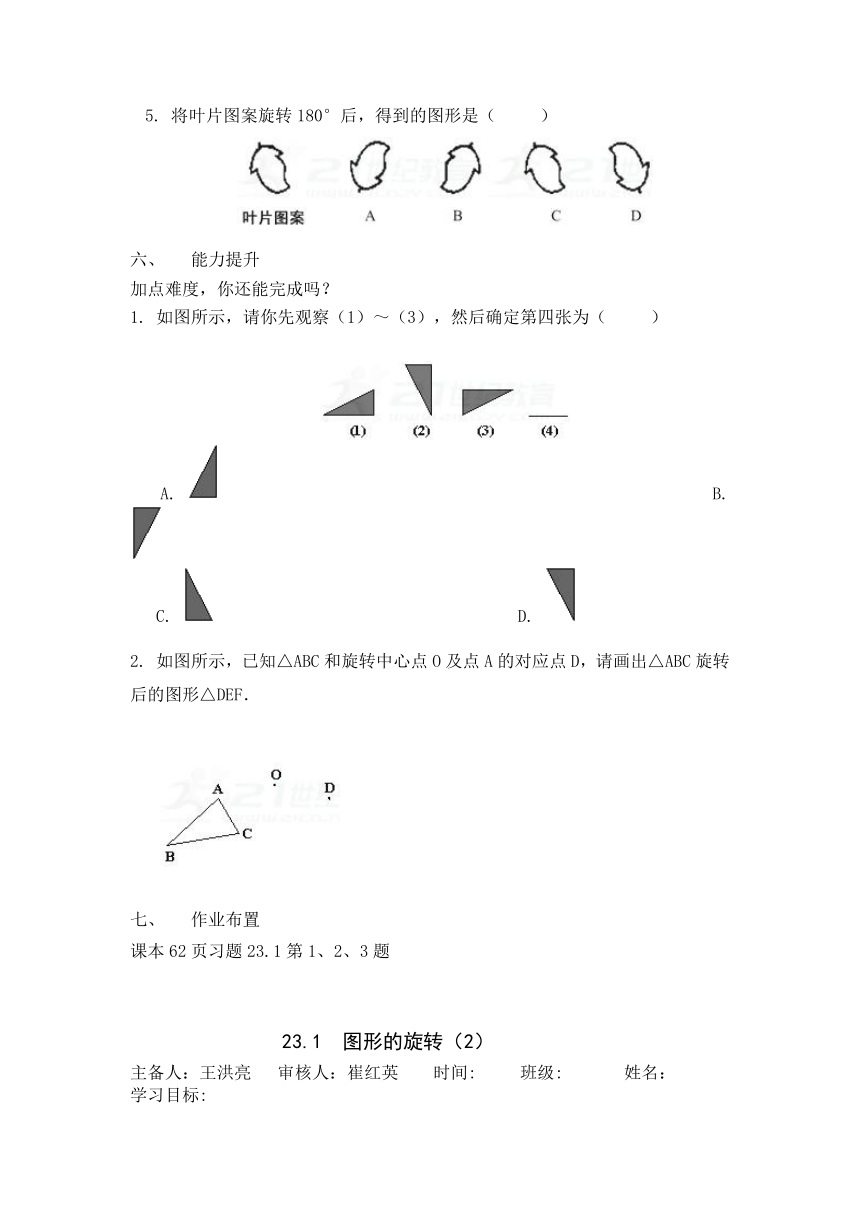
5. 将叶片图案旋转180°后,得到的图形是(?? )
能力提升
加点难度,你还能完成吗?
1. 如图所示,请你先观察(1)~(3),然后确定第四张为(?? )
??????????????? B. ??????????????
C. ????????????????? D.
2. 如图所示,已知△ABC和旋转中心点O及点A的对应点D,请画出△ABC旋转后的图形△DEF.
作业布置
课本62页习题23.1第1、2、3题
23.1 图形的旋转(2)
主备人:王洪亮 审核人:崔红英 时间: 班级: 姓名:
学习目标:
会根据旋转的知识选择不同的旋转中心、不同的旋转角度,设计出美丽的图案.
学习重点和难点
重点:用旋转的有关知识画图.
难点:根据需求设计出美丽的图案.
预习内容
上节课已经学习旋转性质,你能写出旋转性质吗?
(1)________________________________________________
(2)________________________________________________
(3)________________________________________________
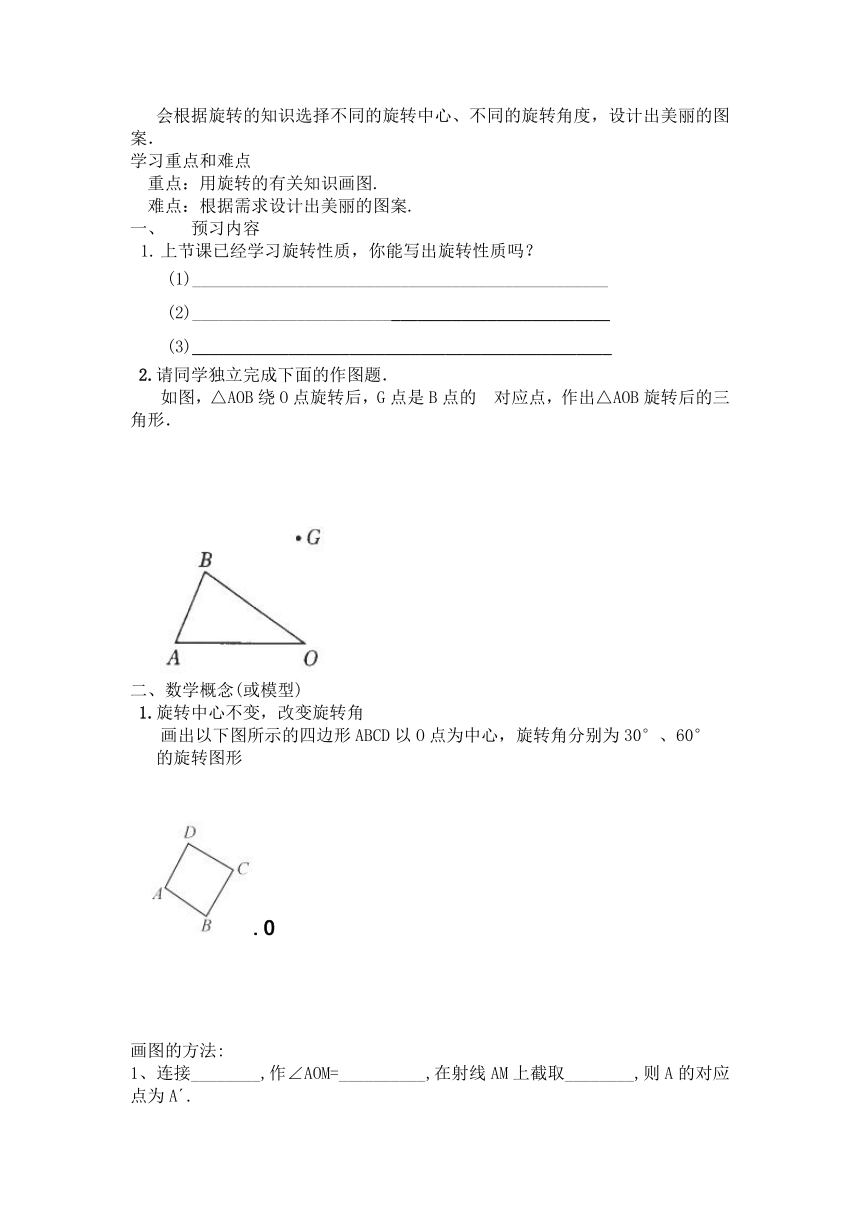
2.请同学独立完成下面的作图题.
如图,△AOB绕O点旋转后,G点是B点的 对应点,作出△AOB旋转后的三角形.
二、数学概念(或模型)
1.旋转中心不变,改变旋转角
画出以下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°
的旋转图形
.O
画图的方法:
1、连接________,作∠AOM=__________,在射线AM上截取________,则A的对应点为A′.
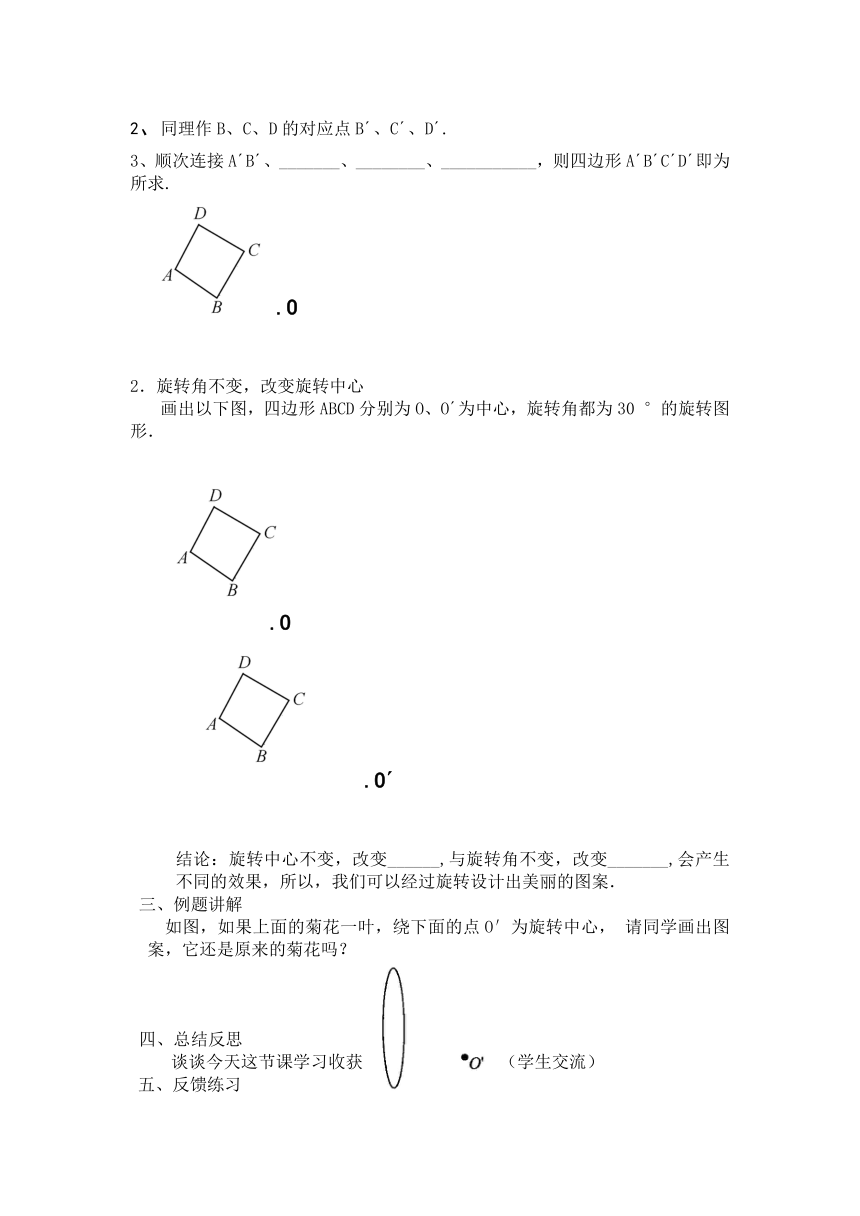
2、同理作B、C、D的对应点B′、C′、D′.
3、顺次连接A′B′、_______、________、___________,则四边形A′B′C′D′即为所求.
.O
2.旋转角不变,改变旋转中心
画出以下图,四边形ABCD分别为O、O′为中心,旋转角都为30°的旋转图形.
.O
.O′
结论:旋转中心不变,改变______,与旋转角不变,改变_______,会产生不同的效果,所以,我们可以经过旋转设计出美丽的图案.
三、例题讲解
如图,如果上面的菊花一叶,绕下面的点O′为旋转中心,请同学画出图案,它还是原来的菊花吗?
四、总结反思
谈谈今天这节课学习收获(学生交流)
五、反馈练习
1.如图,五角星也可以看作是一个三角形绕中心点旋转_______次得到的,每次旋转的角度是________.
2.图形之间的变换关系包括平移、_______、轴对称以及它们的组合变换.
3.如图,过圆心O和图上一点A连一条曲线,将OA绕O点按同一方向连续旋转三次,每次旋转90°,把圆分成四部分,这四部分面积_________.
4. 课本p62练习
六、能力提升
1.如何作出该图案绕O点按逆时针旋转90°的图形.
2.如图,△ABC的直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,求PP′的长.
七、作业布置p63 5 .6 .7 . 8
23.2.1 中心对称(1) 新授课
学习目标
1.了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.
2.通过具体实例认识两个图形关于某一点中心对称的本质:就是一个图形绕一点旋转180°而成.
3.理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.
学习重点和难点
重点:
①用中心对称、对称中心、关于中心对称点的概念解决一些问题.
②中心对称的两条基本性质及其运用.
难点:中心对称的性质及利用以上性质进行作图.
一、预习内容
1、轴对称的定义:如果一个图形沿着一条直线对折后能与另一个图形重合,则称这两个图形关于这条直线对称或轴对称.成轴对称的图形,它们的对应点的连线被对称轴_________.
2、旋转性质:对应点到旋转中心的距离___________对应点与旋转中心所连线段的夹角___________旋转前、后的图形___________.
3、中心对称定义:_____________________________________________.
4、中心对称的性质:_____________________________________________.
二、数学概念(或模型)
1.观察:
如图1把其中一个图案绕点O旋转180°,你有什么发现?
图1
②如图2,线段AC与BD相交于点O,OA=OC,OB=OD,把△OCD绕点O旋转180o,你有什么发现?
图2
老师点评:可以发现,如图所示的两个图案绕O旋转180°都是重合的,即甲图与乙图重合,△OAB与△OCD重合.
归纳:把一个图形绕某一个点旋转180o,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称;点O叫做对称中心;这两个图形中的对应点叫做关于中心的对称点.
2、师生合作,探求新知
[探究]如图,旋转三角板,画关于点O对称的两个三角形;
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A'B'C';
第三步,移开三角板.
这样画出的△ABC与△A'B'C',关于点O对称.分别连接对应点AA'、BB'、CC'.点O在线段AA'上吗?如果在,在什么位置?△ABC与△A'B'C'有什么关系?
[发现]我们可以发现:(1)点O是线段AA'的中点;(2)△ABC≌△A'B'C'.
上述发现可以证明如下.
(1)点A'是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA',所以点O在线段A A'上,且OA=O A',即点O是线段A A'的中点.
同样的,点O也是线段BB'和CC'的中点
(2)在△AOB与△A'OB'中,
OA=OA',OB=OB',∠AOB=∠A'OB',
∴△AOB≌△A'OB'.
∴AB=A'B'.
同理BC=B'C',AC=A'C'.
∴△ABC≌△A'B'C'.
3、理解新知,典例解析
[活动一] 师生合作,归纳出中心对称的性质:
(1) 关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
(2) 关于中心对称的两个图形是全等图形.
[活动二] 中心对称与轴对称进行类比
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻转180度)后重合 图形绕对称中心旋转180度后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心且被对称中心平分
三、例题讲解
例1.(1)如教材图23.2-4,选择点O为对称中心,画出点A关于点O的对称点A’;
(2)如教材图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A’B’C’.
问:1、一个点绕对称中心旋转180o,得到的是一个平角,这表示什么?
2、你是如何理解“对称点所连线段都经过对称中心,而且被对称中心所
3、确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
四、总结反思
谈谈今天这节课学习的收获(自我总结积累,同学交流)
五、反馈练习
A、教材P66练习1、2题
B、如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.
C、如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
六、能力提升
1. 如图,等腰梯形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下列关于点O成中心对称的一组三角形是(? ??).
A.? B. ?
?C.?? D.
2、如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
⑴试判断△BEC是否为等腰三角形,请说明理由?
⑵若AB=1,∠ABE=45°,求BC的长.
⑶在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE
是什么特殊平行四边形,请说明理由.
七、作业布置
1.教科书第69页习题23.2第1题
2.完成练习册习题
23.2.2 中心对称图形 新授课
主备人:甘淑君 审核人:薄光平 时间: 班级: 姓名:
学习目标:
通过自主学习,合作探究,观察比较会说出中心对称图形的定义和性质.
通过练习,能准确判断一个图形是否中心对称图形,并能区分轴对称图形和中心对称图形.
通过观察发现,培养动手动脑,自主探究、合作交流的能力,体验成功的喜悦.
学习重点和难点
重点 :中心对称图形的有关概念及他们的应用
难点:理解中心对称和中心对称图形的区别与联系
预习内容
什么中心对称图形?
轴对称图形与中心对称图形的区别?
3、(1)将线段AB绕着中点旋转180度,你发现了什么?
(2)将平行四边形ABCD绕它的两条对角线的交点O旋转180度,你又发现了什么?
数学概念(或模型)
1、中心对称图形的定义:一个图形绕着某一个点_______________,如果旋转后的图形能够与______________重合,那么这个图形叫做____________,这个点就是它的___________.
2、中心对称和中心对称图形的区别和联系
中心对称
中心对称图形
区别
联系
(提示:可从图形的个数来考虑)
3、根据提示,找出轴对称图形和中心对称图形的异同点
轴对称图形
中心对称图形
关于一条直线对称
沿对称轴翻折对折
对折后与原图形重合
三、例题讲解
1、下列图形中,既是轴对称图形又是中心对称图形的是( )
2、下列图形中,中心对称图形有( )
A 一个 B 两个 C 三个 D四个
四、总结反思
1、谈谈你的收获.
2、你还有什么问题?
五、反馈练习
1.下列几张扑克牌中,中心对称图形的有________张
2.在平面上一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是(??? ) A.180° B.90° C.270° D.360°
3. 下列图案中,既是中心对称又是轴对称的图案是( )
? A ? ? ? ? ? B ? ? ? C ? ? D
六、能力提升 1.某校计划建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等边三角形、等腰梯形、菱形、正五边形等四种方案,你认为符合条件的是( )
A. 等边三角形 B. 等腰梯形 C. 菱形 D. 正五边形
2.常见的图形中,既是轴对称又是中心对称图形的有哪些?它们的对称轴和对称中心分别是什么?
七、作业布置
1.找出26个字母中是中心对称图形的字母
2.完成课本及练习册的习题
23.2.3 关于原点对称的点的坐标 新授课
:
学习目标:
1.举例说明两个关于原点对称的点的坐标特点;
2.会在坐标系中画出已知点(已知图形)关于原点的对称点(对称图形).
重点:能说出关于原点的对称点的坐标特点.
难点:会画关于原点对称的点.
一、预习内容
在图1中画出△ABC关于轴的对称图形,在图2中画出△ABC关于轴的对
称图形.
结论:点A的坐标是(,),则点A关于轴的对称点的坐标是
,点A关于轴的对称点的坐标是 .
二、数学概念(或模型)
1.如图3,写出点A、B、C的坐标,并在直角坐标系中,作出图中已知
点关于原点O的对称点A、B、C,并写出它们的坐标.
2.观察已知点关于原点O的对称点坐标与已知点坐标有什么关系?
结论:两个点关于原点对称时,它们的坐标符号 ,
即点P(,)关于原点的对称点P’( ).
三、例题讲解
例.如图,利用关于原点对称的点的坐标特点,
作出△ABC关于原点对称的图形△A1B1C1
总结反思
1、点A( ,)关于轴的对称点的坐标 ,关于轴的
对称点的坐标 ,关于原点的对称点的坐标 .
2、P(x,y)关于_____的对称点为P'(-x,-y).
反馈练习
下列各点哪两个点关于原点O对称?哪两个点关于轴对称?哪两个点关于轴对称?
A (-4,0),B (3,2),C (3,-2),D (0,-4),E (-3,-2),
F (4,0),G (-2,-3)
六、能力提升
点P(,)关于原点对称的点的坐标为(,-6 ),求的值.
布置作业
1.下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D (2,0), E (0,5),F(-2,1),G(-2,-1).
2.写出下列各点关于原点的对称点A',B',C',D'的坐标:
A(3,1),B(-2,3),C(-1,-2),D(2,-3).
3.若点P(m,1)与点Q(5, n)关于原点对称,则m+n=______
4.点M(5,6)和点N是关于原点对称的两点,则点N在第________象限.
5.△ABC的顶点坐标分别为A(5,0),B(-2,3),C(-1,0).作出与△ABC关于原点O对称
的图形△A'B'C'.
23 旋转 复习课
学习目标:
能结合图形说出旋转中心,旋转角及对应点.
能应用旋转变换解决一些有关图形变换问题.
学习重点和难点
重点:旋转及对应点的有关概念及应用.
难点:旋转的综合应用.
知识梳理
1.在平面内,将一个图形绕一个 沿某个方向转动一个 ,这样的图形运动称为旋转.这个 称为 ,转动的 称为 .
2.旋转性质:(1)对应点到旋转中心的 相等;(2)任意一对对应点与旋转中心所连的 都是旋转角;(3)图形上的每一个点都绕旋转中心沿相同方向转动了 的角度.即旋转角 .
3.在平面内,一个图形绕某个点旋转 ,如果旋转前后的图形互相 ,那么这两个图形叫做中心对称,这个点叫做它的 .
4. 中心对称图形上的每一对对应点所连成的线段都被对称中心 .
5.中心对称与中心对称图形两个概念区别和联系
中心对称是 全等图形之间的 ; 中心对称图形是 图
形本身成对称的 .
中心对称的两个图形性质:
成中心对称的两个图形是 ;成中心对称的两个图形,对称点的连线都经过 ,并且被对称中心 .
6.点P(x,y)关于原点对称的点是________,关于x轴对称的点是______,关于y轴对称的点是_______.
二、例题讲解
例1.确定旋转中心
如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是( )
A.(1,1) B. (1,2) C.(1,3) D.(1,4)
例2.确定旋转角
如图2,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是____,旋转角等于____度,△ADP是______三角形.
例3.旋转相关计算
如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,
则C′B的长为( )
A. B. C. D.1
例4.画旋转图形
如图,△ABC中A(-2,3),B(-3,1),C(-1,2).
(1)将△ABC向右平移4个单位长度,画出平移后的;
(2)画出△ABC关于轴对称的;
(3)将△ABC绕原点旋转180°,画出旋转后的;
(4)在,,中,△______与△______成轴对称,对称轴是______; △______与△______成中心对称,对称中心的坐标是______.
例5.旋转规律探究问题
如图,△AOB为等腰三角形,顶点A的坐标(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B′,点A的对应点A′在x轴上,则点O′的坐标为( )
A.
(,)
B.
(,)
C.
(,)
D.
(,4)
总结反思
谈谈本节课自己的收获.
反馈练习
1、在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是__________
2、如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=_______.
3、如图所示,在△ABC中,∠BAC=90°,AB=AC,点P是△ABC内的一点,且AP=3,将△ABP绕点A旋转后与△ACP′重合,求PP′的长.
能力提升
如图,直线y=x+4与x轴、y轴分别交于A、B两点,
把△A0B绕点A顺时针旋转90°后得到△AO′B′,则
点B′的坐标是__________.
作业布置
下列图形中,中心对称图形有( )
A 一个 B 两个 C 三个 D四个
2.如图,△ABC与△A′B′C′是成中心对称,下列说法不正确的是( )
A.S△ABC=S△A′B′C′ B.AB=A′B′,AC=A′C′,BC=B′C′
C.AB∥A′B′,AC∥A′C′,BC∥B′C′ D.S△ACO=S△A′B′O
3.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A.55° B.45° C.40° D.35°
4..如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.6 B. C. D.3
5.如图,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
23.1 图形的旋转(1) 新授课
学习目标:
通过观察具体实例认识旋转,归纳旋转、旋转中心、旋转角和对应点的概念,
并应用它们解决一些实际问题.
2.探索旋转的性质,会画出旋转后的图形.
学习重点和难点
重点:旋转、对应点的有关概念及其应用.
难点:对旋转现象进行分析研究,旋转后的现象进行探索.
预习内容
钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、风车叶片在转动过程中,其形状、大小、位置是否发生变化呢?
钟表的指针在不停地转动,从3时到5时,时针旋转了多少度?
数学概念
1. 像这样,把一个平面图形绕着平面内某一点O转动一个角度,就叫做图形的 ,点O叫做 ,转动的角叫做 .
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的 .
2. 自学并完成课本60页的探究,归纳旋转的性质:
(1)对应点到旋转中心的距离__________.
(2)对应点与旋转中心所连线段的夹角等于________ .
(3)旋转前、后的图形___________ .
例题讲解
例1: 如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是哪点?旋转方向是什么?旋转角度是多少?点B的对应点是什么?
例2: 如下图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
总结反思
说说你的收获;
你还有什么问题?
反馈练习
1.下列物体的运动不是旋转的是( )
A.坐在摩天轮里的小朋友 B.正在走动的时针
C.骑自行车的人 D.正在转动的风车叶片
2.下列现象中属于旋转的有____个.
地下水位逐年下降;传送带的移动;方向盘的转动;水龙头的转动;钟摆的运动;荡秋千运动.
3.如图,如果把钟表的指针看成四边形AOBC,它绕着O点旋转到四边形DOEF位置,在这个旋转过程中:旋转中心是____,旋转角是_________,经过旋转,点A转到___,点C转到___,点B转到___,线段OA、OB、BC、AC分别转到_____________________,∠A、∠B、∠C分别与___________________是对应角.
如图,将△ABC绕点A逆时针旋转80°得到△AB′C′.
若∠BAC=50°,则∠CAB′的度数为(?? )
A. 30°??? B. 40° C. 50°??? D. 80°
5. 将叶片图案旋转180°后,得到的图形是(?? )
能力提升
加点难度,你还能完成吗?
1. 如图所示,请你先观察(1)~(3),然后确定第四张为(?? )
??????????????? B. ??????????????
C. ????????????????? D.
2. 如图所示,已知△ABC和旋转中心点O及点A的对应点D,请画出△ABC旋转后的图形△DEF.
作业布置
课本62页习题23.1第1、2、3题
23.1 图形的旋转(2)
主备人:王洪亮 审核人:崔红英 时间: 班级: 姓名:
学习目标:
会根据旋转的知识选择不同的旋转中心、不同的旋转角度,设计出美丽的图案.
学习重点和难点
重点:用旋转的有关知识画图.
难点:根据需求设计出美丽的图案.
预习内容
上节课已经学习旋转性质,你能写出旋转性质吗?
(1)________________________________________________
(2)________________________________________________
(3)________________________________________________
2.请同学独立完成下面的作图题.
如图,△AOB绕O点旋转后,G点是B点的 对应点,作出△AOB旋转后的三角形.
二、数学概念(或模型)
1.旋转中心不变,改变旋转角
画出以下图所示的四边形ABCD以O点为中心,旋转角分别为30°、60°
的旋转图形
.O
画图的方法:
1、连接________,作∠AOM=__________,在射线AM上截取________,则A的对应点为A′.
2、同理作B、C、D的对应点B′、C′、D′.
3、顺次连接A′B′、_______、________、___________,则四边形A′B′C′D′即为所求.
.O
2.旋转角不变,改变旋转中心
画出以下图,四边形ABCD分别为O、O′为中心,旋转角都为30°的旋转图形.
.O
.O′
结论:旋转中心不变,改变______,与旋转角不变,改变_______,会产生不同的效果,所以,我们可以经过旋转设计出美丽的图案.
三、例题讲解
如图,如果上面的菊花一叶,绕下面的点O′为旋转中心,请同学画出图案,它还是原来的菊花吗?
四、总结反思
谈谈今天这节课学习收获(学生交流)
五、反馈练习
1.如图,五角星也可以看作是一个三角形绕中心点旋转_______次得到的,每次旋转的角度是________.
2.图形之间的变换关系包括平移、_______、轴对称以及它们的组合变换.
3.如图,过圆心O和图上一点A连一条曲线,将OA绕O点按同一方向连续旋转三次,每次旋转90°,把圆分成四部分,这四部分面积_________.
4. 课本p62练习
六、能力提升
1.如何作出该图案绕O点按逆时针旋转90°的图形.
2.如图,△ABC的直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,求PP′的长.
七、作业布置p63 5 .6 .7 . 8
23.2.1 中心对称(1) 新授课
学习目标
1.了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.
2.通过具体实例认识两个图形关于某一点中心对称的本质:就是一个图形绕一点旋转180°而成.
3.理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.
学习重点和难点
重点:
①用中心对称、对称中心、关于中心对称点的概念解决一些问题.
②中心对称的两条基本性质及其运用.
难点:中心对称的性质及利用以上性质进行作图.
一、预习内容
1、轴对称的定义:如果一个图形沿着一条直线对折后能与另一个图形重合,则称这两个图形关于这条直线对称或轴对称.成轴对称的图形,它们的对应点的连线被对称轴_________.
2、旋转性质:对应点到旋转中心的距离___________对应点与旋转中心所连线段的夹角___________旋转前、后的图形___________.
3、中心对称定义:_____________________________________________.
4、中心对称的性质:_____________________________________________.
二、数学概念(或模型)
1.观察:
如图1把其中一个图案绕点O旋转180°,你有什么发现?
图1
②如图2,线段AC与BD相交于点O,OA=OC,OB=OD,把△OCD绕点O旋转180o,你有什么发现?
图2
老师点评:可以发现,如图所示的两个图案绕O旋转180°都是重合的,即甲图与乙图重合,△OAB与△OCD重合.
归纳:把一个图形绕某一个点旋转180o,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称;点O叫做对称中心;这两个图形中的对应点叫做关于中心的对称点.
2、师生合作,探求新知
[探究]如图,旋转三角板,画关于点O对称的两个三角形;
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A'B'C';
第三步,移开三角板.
这样画出的△ABC与△A'B'C',关于点O对称.分别连接对应点AA'、BB'、CC'.点O在线段AA'上吗?如果在,在什么位置?△ABC与△A'B'C'有什么关系?
[发现]我们可以发现:(1)点O是线段AA'的中点;(2)△ABC≌△A'B'C'.
上述发现可以证明如下.
(1)点A'是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA',所以点O在线段A A'上,且OA=O A',即点O是线段A A'的中点.
同样的,点O也是线段BB'和CC'的中点
(2)在△AOB与△A'OB'中,
OA=OA',OB=OB',∠AOB=∠A'OB',
∴△AOB≌△A'OB'.
∴AB=A'B'.
同理BC=B'C',AC=A'C'.
∴△ABC≌△A'B'C'.
3、理解新知,典例解析
[活动一] 师生合作,归纳出中心对称的性质:
(1) 关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;
(2) 关于中心对称的两个图形是全等图形.
[活动二] 中心对称与轴对称进行类比
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折(翻转180度)后重合 图形绕对称中心旋转180度后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心且被对称中心平分
三、例题讲解
例1.(1)如教材图23.2-4,选择点O为对称中心,画出点A关于点O的对称点A’;
(2)如教材图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A’B’C’.
问:1、一个点绕对称中心旋转180o,得到的是一个平角,这表示什么?
2、你是如何理解“对称点所连线段都经过对称中心,而且被对称中心所
3、确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
四、总结反思
谈谈今天这节课学习的收获(自我总结积累,同学交流)
五、反馈练习
A、教材P66练习1、2题
B、如图,四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答.
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点.
C、如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
六、能力提升
1. 如图,等腰梯形ABCD中,AB∥CD,AB=2CD,AC交BD于点O,点E、F分别为AO、BO的中点,则下列关于点O成中心对称的一组三角形是(? ??).
A.? B. ?
?C.?? D.
2、如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
⑴试判断△BEC是否为等腰三角形,请说明理由?
⑵若AB=1,∠ABE=45°,求BC的长.
⑶在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE
是什么特殊平行四边形,请说明理由.
七、作业布置
1.教科书第69页习题23.2第1题
2.完成练习册习题
23.2.2 中心对称图形 新授课
主备人:甘淑君 审核人:薄光平 时间: 班级: 姓名:
学习目标:
通过自主学习,合作探究,观察比较会说出中心对称图形的定义和性质.
通过练习,能准确判断一个图形是否中心对称图形,并能区分轴对称图形和中心对称图形.
通过观察发现,培养动手动脑,自主探究、合作交流的能力,体验成功的喜悦.
学习重点和难点
重点 :中心对称图形的有关概念及他们的应用
难点:理解中心对称和中心对称图形的区别与联系
预习内容
什么中心对称图形?
轴对称图形与中心对称图形的区别?
3、(1)将线段AB绕着中点旋转180度,你发现了什么?
(2)将平行四边形ABCD绕它的两条对角线的交点O旋转180度,你又发现了什么?
数学概念(或模型)
1、中心对称图形的定义:一个图形绕着某一个点_______________,如果旋转后的图形能够与______________重合,那么这个图形叫做____________,这个点就是它的___________.
2、中心对称和中心对称图形的区别和联系
中心对称
中心对称图形
区别
联系
(提示:可从图形的个数来考虑)
3、根据提示,找出轴对称图形和中心对称图形的异同点
轴对称图形
中心对称图形
关于一条直线对称
沿对称轴翻折对折
对折后与原图形重合
三、例题讲解
1、下列图形中,既是轴对称图形又是中心对称图形的是( )
2、下列图形中,中心对称图形有( )
A 一个 B 两个 C 三个 D四个
四、总结反思
1、谈谈你的收获.
2、你还有什么问题?
五、反馈练习
1.下列几张扑克牌中,中心对称图形的有________张
2.在平面上一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是(??? ) A.180° B.90° C.270° D.360°
3. 下列图案中,既是中心对称又是轴对称的图案是( )
? A ? ? ? ? ? B ? ? ? C ? ? D
六、能力提升 1.某校计划建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等边三角形、等腰梯形、菱形、正五边形等四种方案,你认为符合条件的是( )
A. 等边三角形 B. 等腰梯形 C. 菱形 D. 正五边形
2.常见的图形中,既是轴对称又是中心对称图形的有哪些?它们的对称轴和对称中心分别是什么?
七、作业布置
1.找出26个字母中是中心对称图形的字母
2.完成课本及练习册的习题
23.2.3 关于原点对称的点的坐标 新授课
:
学习目标:
1.举例说明两个关于原点对称的点的坐标特点;
2.会在坐标系中画出已知点(已知图形)关于原点的对称点(对称图形).
重点:能说出关于原点的对称点的坐标特点.
难点:会画关于原点对称的点.
一、预习内容
在图1中画出△ABC关于轴的对称图形,在图2中画出△ABC关于轴的对
称图形.
结论:点A的坐标是(,),则点A关于轴的对称点的坐标是
,点A关于轴的对称点的坐标是 .
二、数学概念(或模型)
1.如图3,写出点A、B、C的坐标,并在直角坐标系中,作出图中已知
点关于原点O的对称点A、B、C,并写出它们的坐标.
2.观察已知点关于原点O的对称点坐标与已知点坐标有什么关系?
结论:两个点关于原点对称时,它们的坐标符号 ,
即点P(,)关于原点的对称点P’( ).
三、例题讲解
例.如图,利用关于原点对称的点的坐标特点,
作出△ABC关于原点对称的图形△A1B1C1
总结反思
1、点A( ,)关于轴的对称点的坐标 ,关于轴的
对称点的坐标 ,关于原点的对称点的坐标 .
2、P(x,y)关于_____的对称点为P'(-x,-y).
反馈练习
下列各点哪两个点关于原点O对称?哪两个点关于轴对称?哪两个点关于轴对称?
A (-4,0),B (3,2),C (3,-2),D (0,-4),E (-3,-2),
F (4,0),G (-2,-3)
六、能力提升
点P(,)关于原点对称的点的坐标为(,-6 ),求的值.
布置作业
1.下列各点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D (2,0), E (0,5),F(-2,1),G(-2,-1).
2.写出下列各点关于原点的对称点A',B',C',D'的坐标:
A(3,1),B(-2,3),C(-1,-2),D(2,-3).
3.若点P(m,1)与点Q(5, n)关于原点对称,则m+n=______
4.点M(5,6)和点N是关于原点对称的两点,则点N在第________象限.
5.△ABC的顶点坐标分别为A(5,0),B(-2,3),C(-1,0).作出与△ABC关于原点O对称
的图形△A'B'C'.
23 旋转 复习课
学习目标:
能结合图形说出旋转中心,旋转角及对应点.
能应用旋转变换解决一些有关图形变换问题.
学习重点和难点
重点:旋转及对应点的有关概念及应用.
难点:旋转的综合应用.
知识梳理
1.在平面内,将一个图形绕一个 沿某个方向转动一个 ,这样的图形运动称为旋转.这个 称为 ,转动的 称为 .
2.旋转性质:(1)对应点到旋转中心的 相等;(2)任意一对对应点与旋转中心所连的 都是旋转角;(3)图形上的每一个点都绕旋转中心沿相同方向转动了 的角度.即旋转角 .
3.在平面内,一个图形绕某个点旋转 ,如果旋转前后的图形互相 ,那么这两个图形叫做中心对称,这个点叫做它的 .
4. 中心对称图形上的每一对对应点所连成的线段都被对称中心 .
5.中心对称与中心对称图形两个概念区别和联系
中心对称是 全等图形之间的 ; 中心对称图形是 图
形本身成对称的 .
中心对称的两个图形性质:
成中心对称的两个图形是 ;成中心对称的两个图形,对称点的连线都经过 ,并且被对称中心 .
6.点P(x,y)关于原点对称的点是________,关于x轴对称的点是______,关于y轴对称的点是_______.
二、例题讲解
例1.确定旋转中心
如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是( )
A.(1,1) B. (1,2) C.(1,3) D.(1,4)
例2.确定旋转角
如图2,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是____,旋转角等于____度,△ADP是______三角形.
例3.旋转相关计算
如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,
则C′B的长为( )
A. B. C. D.1
例4.画旋转图形
如图,△ABC中A(-2,3),B(-3,1),C(-1,2).
(1)将△ABC向右平移4个单位长度,画出平移后的;
(2)画出△ABC关于轴对称的;
(3)将△ABC绕原点旋转180°,画出旋转后的;
(4)在,,中,△______与△______成轴对称,对称轴是______; △______与△______成中心对称,对称中心的坐标是______.
例5.旋转规律探究问题
如图,△AOB为等腰三角形,顶点A的坐标(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B′,点A的对应点A′在x轴上,则点O′的坐标为( )
A.
(,)
B.
(,)
C.
(,)
D.
(,4)
总结反思
谈谈本节课自己的收获.
反馈练习
1、在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是__________
2、如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=_______.
3、如图所示,在△ABC中,∠BAC=90°,AB=AC,点P是△ABC内的一点,且AP=3,将△ABP绕点A旋转后与△ACP′重合,求PP′的长.
能力提升
如图,直线y=x+4与x轴、y轴分别交于A、B两点,
把△A0B绕点A顺时针旋转90°后得到△AO′B′,则
点B′的坐标是__________.
作业布置
下列图形中,中心对称图形有( )
A 一个 B 两个 C 三个 D四个
2.如图,△ABC与△A′B′C′是成中心对称,下列说法不正确的是( )
A.S△ABC=S△A′B′C′ B.AB=A′B′,AC=A′C′,BC=B′C′
C.AB∥A′B′,AC∥A′C′,BC∥B′C′ D.S△ACO=S△A′B′O
3.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
A.55° B.45° C.40° D.35°
4..如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.6 B. C. D.3
5.如图,四边形ABCD的∠BAD=∠C=90°,AB =AD ,AE⊥ BC 于E,△BEA旋转一定角度后能与△DFA重合.
旋转中心是哪一点?
旋转了多少度?
若AE=5cm,求四边形ABCD的面积.
同课章节目录
