2.2平方根(2课时教学详案）

2　平方根
1.了解数的算术平方根、平方根的概念,会用根号表示一个数的算术平方根和平方根.
2.了解开方与平方是互逆运算,会利用平方运算求某些非负数的算术平方根和平方根.
通过教学过程的参与,培养学生学习的主动性,提高数学表达和运算能力.
1.通过与“加法的逆运算是减法、乘法的逆运算
是除法”作类比,让学生体会平方和开方互为逆运算的同时,领会数学中处处蕴含着辩证法.
2.使学生通过开方运算的学习,解决实际生活中的一些具体问题.
【重点】
1.数的算术平方根、平方根的概念,会用根号表示一个数的算术平方根和平方根.
2.()2=a(a≥0)的得出和应用.
【难点】
1.利用这个互逆的关系求某些非负数的算术平方根和平方根.
2.()2=a(a≥0)和=|a|的区别和联系.
第课时
1.了解数的算术平方根的概念,会用根号表示一个数的算术平方根.
2.了解一个正数的算术平方根与平方是互逆的运算,会利用这个互逆的关系求某些非负数的算术平方根.
在合作交流等活动中,培养合作精神和创新精神.
积极参与教学活动,发展对数学的好奇心和求知欲.
【重点】　算术平方根的概念、性质,会用根号表示一个数的算术平方根.
【难点】　对算术平方根的概念和性质的理解.
【教师准备】　挂图、多媒体课件.
【学生准备】　复习无理数的概念.
　　[过渡语]　知道无理数的存在,上节给出的问题我们需要解决了.
导入一:
上节课学习了无理数,了解到无理数产生的实际背景和引入的必要性,掌握了无理数的概念,知道有理数和无理数的区别是:有理数是有限小数或无限循环小数,无理数是无限不循环小数.比如上一节课我们做过的:由两个边长为1的小正方形,通过剪一剪,拼一拼,得到一个边长为a的大的正方形,那么有a2=2,a=　　　　,2是有理数,而a是无理数.在前面我们学过:若x2=a,则a叫x的平方,反过来x叫a的什么呢?本节课我们一起来学习.?
导入二:
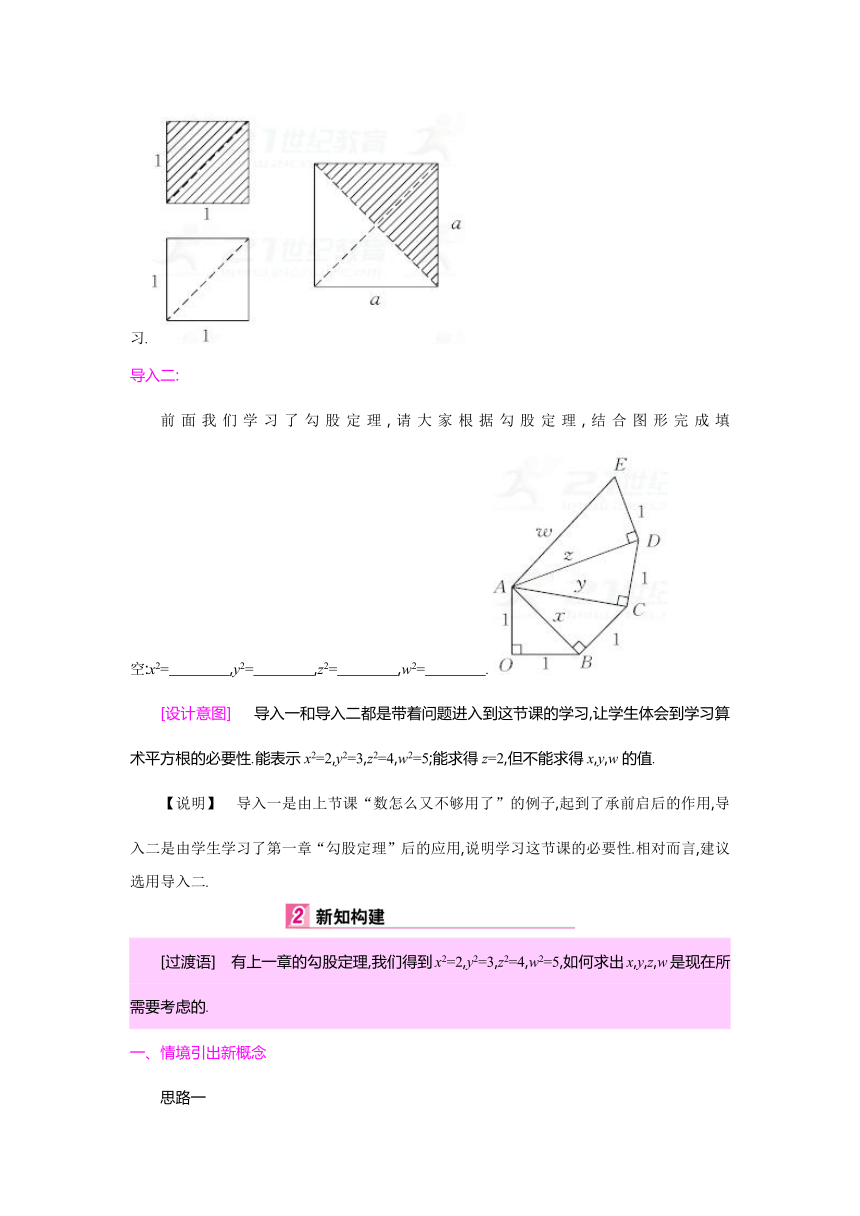
前面我们学习了勾股定理,请大家根据勾股定理,结合图形完成填空:x2=　　　　,y2=　　　　,z2=　　　　,w2=　　　　.?
[设计意图]　 导入一和导入二都是带着问题进入到这节课的学习,让学生体会到学习算术平方根的必要性.能表示x2=2,y2=3,z2=4,w2=5;能求得z=2,但不能求得x,y,w的值.
【说明】　导入一是由上节课“数怎么又不够用了”的例子,起到了承前启后的作用,导入二是由学生学习了第一章“勾股定理”后的应用,说明学习这节课的必要性.相对而言,建议选用导入二.
　　[过渡语]　有上一章的勾股定理,我们得到x2=2,y2=3,z2=4,w2=5,如何求出x,y,z,w是现在所需要考虑的.
一、情境引出新概念
思路一
x2=2,y2=3,z2=4,w2=5,已知幂和指数,求底数x,y,z,w,你能求出来吗?
思路二
在七年级学习有理数的乘方时,知道自然数的平方,比如12=1,22=4,32=9,…,但是,你能找到哪个数的平方是2吗?哪个数的平方是3吗?哪个数的平方是5吗?那你能估计一下吗?
[设计意图]　让学生体验概念形成过程,感受到概念引入的必要性.学生可以估算出x,y是1到2之间的数,w是2到3之间的数,但无法表示x,y,w,从而激发学生继续往下学习的兴趣,进而引入新的运算——开方.
【说明】　无论是导入一,还是导入二,都会激发学生继续往下学习的兴趣,都可以提出同样的问题“已知幂和指数,求底数,你能求出来吗?”
二、在上面思考的基础上,明晰概念
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根,记作,读作“根号a”.
特别地,我们规定:0的算术平方根是0,即=0.
[设计意图]　对算术平方根概念的认识,了解算术平方根的概念,知道平方运算和求正数的算术平方根是互逆的.
三、例题讲解
　求下列各数的算术平方根.
(1) 900;　(2) 1;　(3);　(4) 14.
〔解析〕　体验求一个正数的算术平方根的过程,利用平方运算求一个正数的算术平方根的方法,让学生明白有的正数的算术平方根可以开出来,有的正数的算术平方根只能用根号表示,如14的算术平方根是.
解:(1)因为302=900,所以900的算术平方根是30,即=30.
(2)因为12=1,所以1的算术平方根是1,即=1.
(3)因为,所以 的算术平方根是, 即 .
(4)14的算术平方根是.
[设计意图]　通过对例题的解答,加深学生对算术平方根概念的理解,会求一个正数的算术平方根,更进一步了解算术平方根的性质:一个正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根.体验求一个正数算术平方根的过程,并为下面的实验应用奠定良好的基础.
　自由下落物体下落的距离s(m)与下落时间t(s)的关系为s=4.9t2.有一铁球从19.6 m高的建筑物上自由下落,到达地面需要多长时间?
〔解析〕　用算术平方根的知识解决实际问题.利用等式的性质将s=4.9t2进行变形,再用求算术平方根的方法求得题目的解.
解:将s=19.6代入公式s=4.9t2,
得t2=4,所以t==2(s).
即铁球到达地面需要2 s.
【说明】　强调实际问题t是正数,用的是算术平方根,此题是为得出下面的结论做铺垫的.观察我们刚才求出的算术平方根有什么特点.
[设计意图]　让学生认识到算术平方根定义中的两层含义:中的a是一个非负数,a的算术平方根也是一个非负数,负数没有算术平方根.这也是算术平方根的性质——双重非负性.再一次深入地认识算术平方根的概念,明确只有非负数才有算术平方根.
[知识拓展]　算术平方根有如下性质:
(1)一个正数a有一个算术平方根,就是.
(2)0有一个算术平方根,就是0.
(3)负数没有算术平方根.
(4)只要有意义,就表示一个非负数,即≥0.
(5)中的a是一个非负数,即a≥0.
1.算术平方根的概念,式子中的双重非负性:一是a≥0,二是≥0.
2.算术平方根的性质:一个正数的算术平方根是一个正数;0的算术平方根是0;负数没有算术平方根.
3.求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
1.若一个数的算术平方根是,那么这个数是　　　　.?
答案:7
2.的算术平方根是　　　　.?
答案:
3.的算术平方根是　　　　.?
答案:
4.若=2,则(m+2)2=　　　　.?
解析:本题考查算术平方根的定义,掌握表示方法和实质是关键.故填16.
5.求下列各数的算术平方根.
36,,15,0.64,10-4,,.
解:=6, ,,=0.8,=10-2, , =1.
6.如图所示,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为5.5米,地面固定点C到帐篷支撑竿底部B的距离是4.5米,则帐篷支撑竿的高是多少米?
解:由题意得 AC=5.5米,BC=4.5米,∠ABC=90°,在RtΔABC中,由勾股定理得AB=(米).所以帐篷支撑竿的高是米.
第1课时
1.情境引出新概念.
2.在上面思考的基础上,明晰概念.
3.例题讲解.
一、教材作业
【必做题】
教材第27页随堂练习第1,3题.
【选做题】
教材第27页习题2.3第3,4题.
二、课后作业
【基础巩固】
1.填空.
(1)81的算术平方根是　　　　.?
(2)0.1是　　　　的算术平方根.?
(3)一个正方形的面积变为原来的4倍,它的边长变为原来的　　　　倍.?
(4)一个正方形的面积变为原来的9倍,它的边长变为原来的　　　　倍.?
(5)一个圆的面积变为原来的n倍, 它的半径变为原来的　　　　倍.?
2.求下列各数的算术平方根.
1.96　　　106　　　121
【能力提升】
3.的算术平方根　　　　,若5是a+1的算术平方根,则a=　　　　.?
4.一个数的算术平方根等于它本身的2倍,这个数是　　　　.?
5.x为何值时, 有意义?
【拓展探究】
6.已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是 (　　)
A.a+1　　　　　B.
C.a2+1 D.
7.求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n
16
0.16
0.0016
1600
160000
…
4
0.4
0.04
40
400
…
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题.
已知≈1.435,求下列各数的算术平方根:①0.0206;②206;③20600.
【答案与解析】
1.(1)9　(2)0.01　(3)2　(4)3　(5)(解析:设现在圆的半径为R,原来圆的半径为r,则πR2=nπr2,所以R=r.)
2.解:=1.4,,=11.
3.2　24(解析:=4,=2;52=a+1,a=24.)
4.0或4(解析:设这个数为x,则=2x,所以x=4x2,解得x=0或x=4.)
5.解:由题意得-≥0,所以x≤0.
6.D(解析:一个自然数的算术平方根是a,这个自然数是a2,故该自然数的下一个自然数是a2+1,其算术平方根是.)
7.解析:(1)从被开方数和算术平方根的小数点的移动位数考虑解答.(2)根据(1)中的规律解答即可.解:(1)被开方数扩大或缩小102n倍,非负数的算术平方根就相应地扩大或缩小10n倍;或者说成被开方数的小数点向左或向右移动2n位,算术平方根的小数点就向左或向右移动n位.　(2)①=0.1435.②=14.35.③=143.5.
本节课通过勾股定理和七年级学过的有理数的平方引入,在学生已有知识的基础上,引入新概念、算术平方根的本质特征.通过练习,可以使学生掌握和理解.
由于学生是第一次接触算术平方根,时间短,可
能有的学生不能真正地理解和掌握,或者不能掌握实质,给以后的学习带来很多麻烦.
在教学中,根据学生的实际情况,在学有余力的情况下,可以对的双重非负性的知识进行适当的拓展.
随堂练习(教材第27页)
1.解:=6,　,,=0.9,.
2.解:AB=.
3.解:AB==4.8(m).
习题2.3(教材第27页)
1.解:(1)=7.　(2)　.　(3)=0.3.　(4)-=-8.
2.解:它们的算术平方根依次是11,,1.4,103.
3.解:每块地砖的边长是=0.3(m).
4.解:设原正方形的边长为a,变化后的正方形的边长为x.①x2=4a2,所以x=2a(负值舍),故边长变为原来的2倍.②x2=9a2,所以x=3a(负值舍),故边长变为原来的3倍.③x2=100a2,所以x=10a(负值舍),故边长变为原来的10倍.④x2=na2,所以x=a(负值舍),故边长变为原来的倍.
　求下列各数的算术平方根.
(1);　　　　 (2)104;
(3);　　　(4)(3-π)2.
〔解析〕　前三个是以不同形式给出的几个数,必须先化简,如(1)中=4,(2)中104=10000,(3)中|-169|=169,然后求它们的平方根,(4)题要特别注意判断π与3的大小.
解:(1)因为=4,
所以的算术平方根是2.
(2)因为104=10000,
所以104的算术平方根为100.
(3)因为|-169|=169,
所以|-169|的算术平方根为13.
(4)因为π>3,所以π-3>0,
所以(3-π)2的算术平方根为π-3.
[解题策略]　出现求类似(3-π)2形式的数的算术平方根时,注意判断括号内数的正负.求一个式子的算术平方根时,应先求出这个式子的值,再求这个值的算术平方根.
第课时
1.了解数的平方根、开平方的概念,会用根号表示一个非负数的平方根.
2.了解开方与乘方是互逆的运算,会利用这个互逆的关系求某些非负数的平方根.
经历平方根概念的形成过程,发展求同和求异的思想,通过比较,提高思考问题、辨析问题的能力.
在学习的过程中,养成严谨的科学态度.
【重点】
1.数的平方根的概念,会用根号表示一个非负数的平方根.
2.=a(a≥0)的得出和应用.
【难点】
1.开方与乘方是互逆的运算,会利用这个互逆的关系求某些非负数的平方根.
2.=a(a≥0)和=|a|的区别和联系.
【教师准备】　练习题的多媒体课件.
【学生准备】　复习算术平方根的概念.
　　[过渡语]　上节学习了算术平方根,首先我们复习一下.
导入一:
1.什么叫算术平方根?
3的平方等于9,那么9的算术平方根就是3.
的平方等于 ,那么的算术平方根就是.
展厅的地面为正方形,其面积为49平方米,则其边长为7米.
2.到目前为止,我们已学过哪些运算?这些运算之间的关系如何?
平方有没有逆运算?
平方与算术平方根之间是什么关系?
【例如】　正方形ABCD的面积为1,则边长为1.将它扩展,若其面积变为原来的2倍,则边长为;若其面积变为原来的3倍,则边长为;若其面积变为原来的n倍,则边长为.
导入二:
【问题】　平方等于9,,49的数还有吗?
回忆在七年级学习有理数的平方时,我们是如何找到平方等于9,,49的数的?根据平方的定义,32=9,(-3)2=9,,,72=49,(-7)2=49.
[设计意图]　这一环节主要是复习旧知识和提出问题,由上节课的“算术平方根”的求法使学生能明白“平方”和“算术平方根”的关系,让学生在几何图形中认识、熟悉它们的互化关系.并把上节课的思考题制作成Flash情景引入,增加动画效果. 借助多媒体吸引学生的注意力,激发学生的学习兴趣.
【说明】　数学知识源于生活,并服务于生活.这两种方法通过生活中的具体问题激发学生的学习兴趣,并让他们产生解决问题的强烈欲望.
一、共同探究
思路一
　　[过渡语]　根据我们的实践,平方为9的数不只有3,那请同学们填写下面的空.
填空.
形成概念:
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x就叫做a的平方根(也叫做二次方根).
表达式为:若x2=a,则x叫做a的平方根.记作±.
【例如】　(±4)2 =16,则+4和-4都是16的平方根,即16的平方根是±4.4是16的算术平方根.
【结论】　一个正数有两个平方根;0只有一个平方根,它是0本身;负数没有平方根.
【定义】　求一个数a的平方根的运算,叫做开平方,a叫做被开方数.
思路二
前面我们学习算术平方根,知道9的算术平方根是3,根据七年级我们学过的平方的意义,-3的平方也是9,也就是说,平方为9的数有两个:3和-3.一个正数a的算术平方根有一个,通过进一步的思考知道平方为a的数有两个,另外一个我们也不能把它给丢了,今天再学习一个平方根的概念.
　　[过渡语]　知道了平方根的定义,和我们上一节学习的算术平方根的联系和区别是什么呢?
给出几组具体的数据,由平方探知开平方与平方的互逆关系.
平方根与算术平方根的联系与区别.
【联系】
1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3.0的平方根是0,算术平方根也是0.
【区别】
1.个数不同:一个正数有两个平方根,但只有一个算术平方根.
2.表示法不同:平方根表示为 ±,而算术平方根表示为.
[设计意图]　形成“平方根”的概念.在列举一些具体数据的感性认识的基础上,由平方运算反推出平方根的概念和定义,并让学生非常熟练地进行平方和平方根之间的互化,并明白它们之间的互逆关系,辨析概念 “平方根”与 “算术平方根”的区别与联系,使之与上节课紧密联系. 由于遵循了从具体到抽象的过程,注重学生原有认知基础的回顾,并和原有的概念进行了比较与辨析,因此,学生对这一抽象的概念掌握得比较牢靠.
【说明】　平方根与算术平方根的区别是本节课的一大难点,也是学生经常容易出错的地方.对这两个概念加以比较与区别有利于学生的理解与掌握.
二、例题讲解
(教材第28页例3)求下列各数的平方根.
(1)64;　(2);　(3)0.0004;
(4)(-25)2;　(5) 11.
解:(1)因为(±8)2=64,所以64的平方根是±8,即±=±8.
(2)因为,所以的平方根是±,即± =±.
(3)因为(±0.02)2=0.0004,所以0.0004的平方根是±0.02,即±=±0.02.
(4)因为(±25)2=(-25)2,所以(-25)2的平方根是±25, 即±=±25.
(5)11的平方根是±.
[设计意图]　通过例题的讲解,要求学生能正确掌握平方根的文字说理及符号化的表达.能熟练地求出一个数的平方根,然后由题中的数据探索出正数、0、负数的平方根的个数.
[知识拓展]　平方根的性质:(1)一个正数a有两个平方根,一个是a的算术平方根“”,另一个是“-”,它们互为相反数,合起来记作“±”,读作“正、负根号a”.例如:5的平方根是±.(2)0的平方根是0.(3)负数没有平方根.
1.平方根的概念:若x2=a,则x叫做a的平方根,x=±.
2.平方根的个数:正数有2个平方根,0的平方根是0,负数没有平方根.
3.平方与开平方之间的关系.
4.求平方根的方法:求一个数的平方根就是转化为寻找哪个数的平方等于这个数.
1.(-5)2的平方根是　　　　,的算术平方根是　　　　,的平方根是　　　　.?
答案:±5　3　±
2.()2=　　　　,=　　　　,±=　　　　,=　　　　.?
答案:64　5　±8　0.2
3.=　　　　,当a≥0时,()2=　　　　.?
答案:|a|　a
4.下列说法正确的是　　　　.?
①-3是的一个平方根;②25的平方根是5;③-36的平方根是-6;④平方根等于0的数是0;⑤64的平方根是8.
答案:①④
5.下列说法不正确的是 (　　)
A.0的平方根是0
B.(-2)2的平方根是±2
C.负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
答案:C
第2课时
1.平方根.
2.平方根与算术平方根的联系与区别.
3.例题讲解.
一、教材作业
【必做题】
教材第29页随堂练习第1,2题.
【选做题】
教材第29页习题2.4第6题.
二、课后作业
【基础巩固】
1.代数式x2+1,,|y|,(m-1)2中,一定是正数的有 (　　)
A.1个　　　B.2个　　　C.3个　　　D.4个
2.下列说法中,错误的是 (　　)
A.4的算术平方根是2
B.的平方根是±3
C.121的平方根是±11
D.-1的平方根是±1
3.(-6)2的算术平方根是　　　　.?
4.2的平方根是　　　　.?
5.若=-a,则a　　　　0.?
6.求2的平方根和算术平方根.
【能力提升】
7.求下列各式中的x.
(1)(x-1)2=4;　(2)4x2-2=14.
8.5+的小数部分为a,5-的小数部分为b,求a+b的值.
【拓展探究】
9.如果一个非负数的平方根是2a+1与a-3,求a的值.
10.已知ΔABC的三边长分别为a,b,c,且a,b,c满足+|b-4|+c2-6c+9=0,试判断ΔABC的形状,并求ΔABC的周长.
11.已知实数a,b满足b2++9=6b.
(1)若a,b为ΔABC的两边长,求第三边长c的取值范围;
(2)若a,b为ΔABC的两边长,第三边长c等于5,求ΔABC的面积.
【答案与解析】
1.A(解析:只有x2+1一定是正数.)
2.D(解析:负数没有平方根.)
3.6(解析:(-6)2=36.)
4.±(解析:根据平方根的定义解题.)
5.≤(解析:当a≥0时,=a;当a<0时,=-a.等号在a<0上也可以.)
6.解:2,的平方根为±,的算术平方根为.
7.解:(1)x-1=±2,所以x=3或-1.　(2)4x2=16,x2=4,x=±2.
8.解:因为3<<4 ,所以5+的整数部分为8,5-的整数部分为1,所以5+的小数部分a=5+-8=-3,5-的小数部分b=5--1=4-,所以a+b=-3+4-=1.
9.解:因为一个非负数的平方根是2a+1与a-3,由平方根的性质,得2a+1+a-3=0,所以a=.
10.解:ΔABC为等腰三角形.理由如下:由+|b-4|+c2-6c+9=0,得+|b-4|+(c-3)2=0,由非负数的性质,得a-3=0,b-4=0,c-3=0,解得a=3,b=4,c=3,所以ΔABC为等腰三角形,周长为10.
11.解:(1)b2++9=6b,整理得(b-3)2+=0,所以b=3,a=4,所以第三边长c的取值范围为1本节课注重概念的形成过程,让学生在概念的形成过程中,逐步理解所学的概念.经过分析,掌握其本质特征、概念的形成过程,对提高学生的思维水平是很必要的.所以在学习平方根的概念时,对正数有两个平方根学生不太容易接受,往往丢掉负的平方根,为此,在平方根的引入时,多提了一些具体的问题,引起学生的思考,让学生从具体的例子中抽象出初步的平方根的概念.
本节课只安排了一道例题和几个想一想,围绕“平方根”这一知识点进行各种题型的变式练习,可能有的学生不能很好地掌握平方根这一概念.
“平方根”这一知识点不易理解和掌握,对此可以进行各种题型的变式练习.当然,选题要有层次,有梯度.
随堂练习(教材第29页)
1.解:±=±1.2,±=0,±,± =±,±=±21,±=±14,±=±.
2.(1)±5　(2)5　(3)5
3.解:当a=5,b=12时,=13.
习题2.4(教材第29页)
1.解:它们的平方根依次是±13,±10-3,±,±,±.
2.提示:(1)19.　(2)-11.　(3)14或-14.
3.解:(1)x=±.　(2)x=±.
4.解:(1)4.　(2)4.　(3)0.8.
5.解:当c=25,b=24时,　=　=7.
6.解:不一定.当a≥0时,=a;当a<0时,=-a.
　已知+(y+2)2+ =0,求x+y+z的值.
解:因为≥0,(y+2)2≥0, ≥0,且+(y+2)2+ =0 ,所以=0,(y+2)2=0, =0,解得x=,y=-2,z=-,所以x+y+z=-3.
　若x,y满足+y=5,求xy的值.
解:因为2x-1≥0,1-2x≥0,
所以 2x-1=0,解得 x=.
当 x=时,y=5,
所以 xy=×5=.
　求x+=5中的x.
解:因为x-5≥0,=5-x≥0 ,
所以x=5.
　ΔABC的三边长分别为a,b,c,且a,b满足+b2-4b+4=0,求c的取值范围.
解:由+b2-4b+4=0,
可得+(b-2)2=0.
因为 ≥0,(b-2)2≥0,
所以=0,(b-2)2=0,所以a=1,b=2.
由三角形三边关系定理有b-a　设a,b,c都是实数,且满足(2-a)2++|c+8|=0,ax2+bx+c=0,求式子x2+2x的算术平方根.
解:由题意得2-a=0,a2+b+c=0,c+8=0,
∴a=2,c=-8,b=4,
∴2x2+4x-8=0,
∴x2+2x=4,
∴式子x2+2x的算术平方根为2.