24.1 圆的有关性质培优提高试题
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
九上数学培优提高 第二十四章 圆 第一节 圆的有关性质
一.选择题(共10小题)
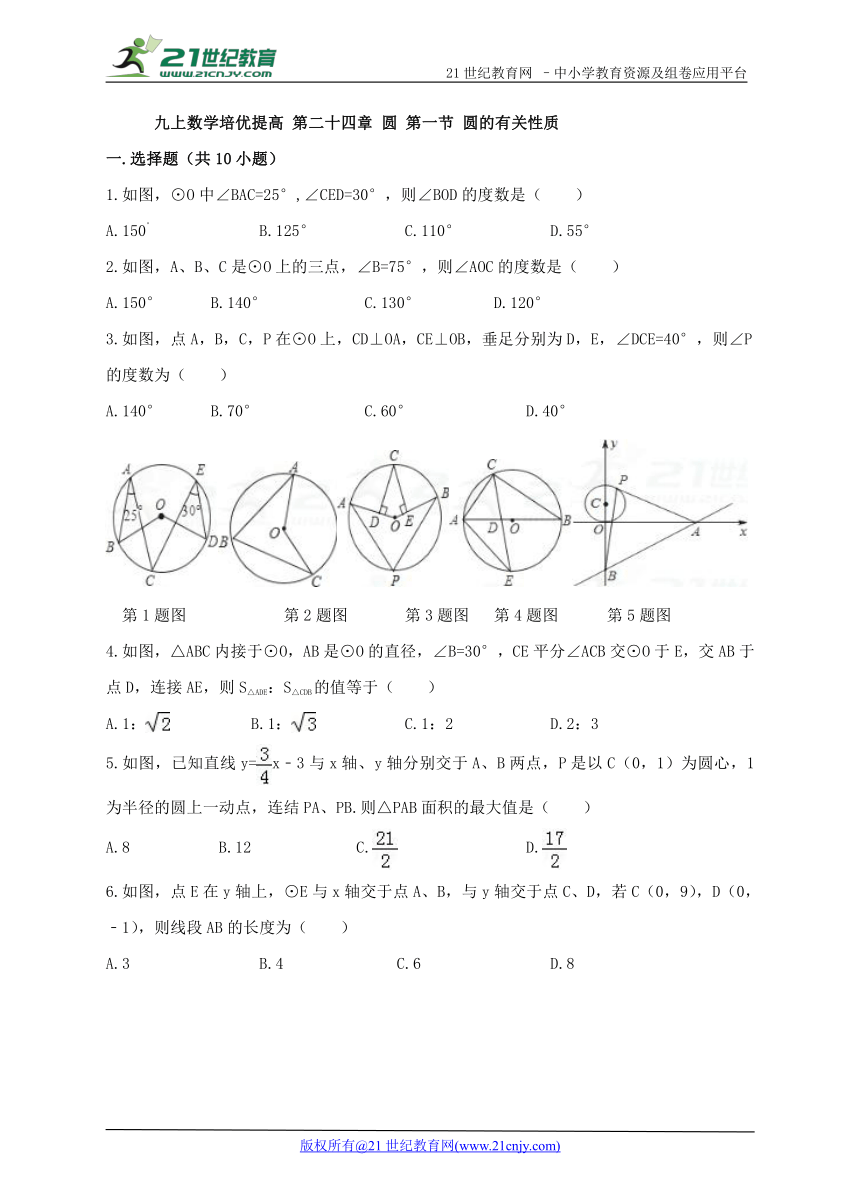
1.如图,⊙O中∠BAC=25°,∠CED=30°,则∠BOD的度数是( )
A.150° B.125° C.110° D.55°
2.如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
A.150° B.140° C.130° D.120°
3.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )21cnjy.com
A.140° B.70° C.60° D.40°21·cn·jy·com
第1题图 第2题图 第3题图 第4题图 第5题图
4.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )www.21-cn-jy.com
A.1: B.1: C.1:2 D.2:3
5.如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.8 B.12 C. D.
6.如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,9),D(0,﹣1),则线段AB的长度为( )2·1·c·n·j·y
A.3 B.4 C.6 D.8【来源:21·世纪·教育·网】
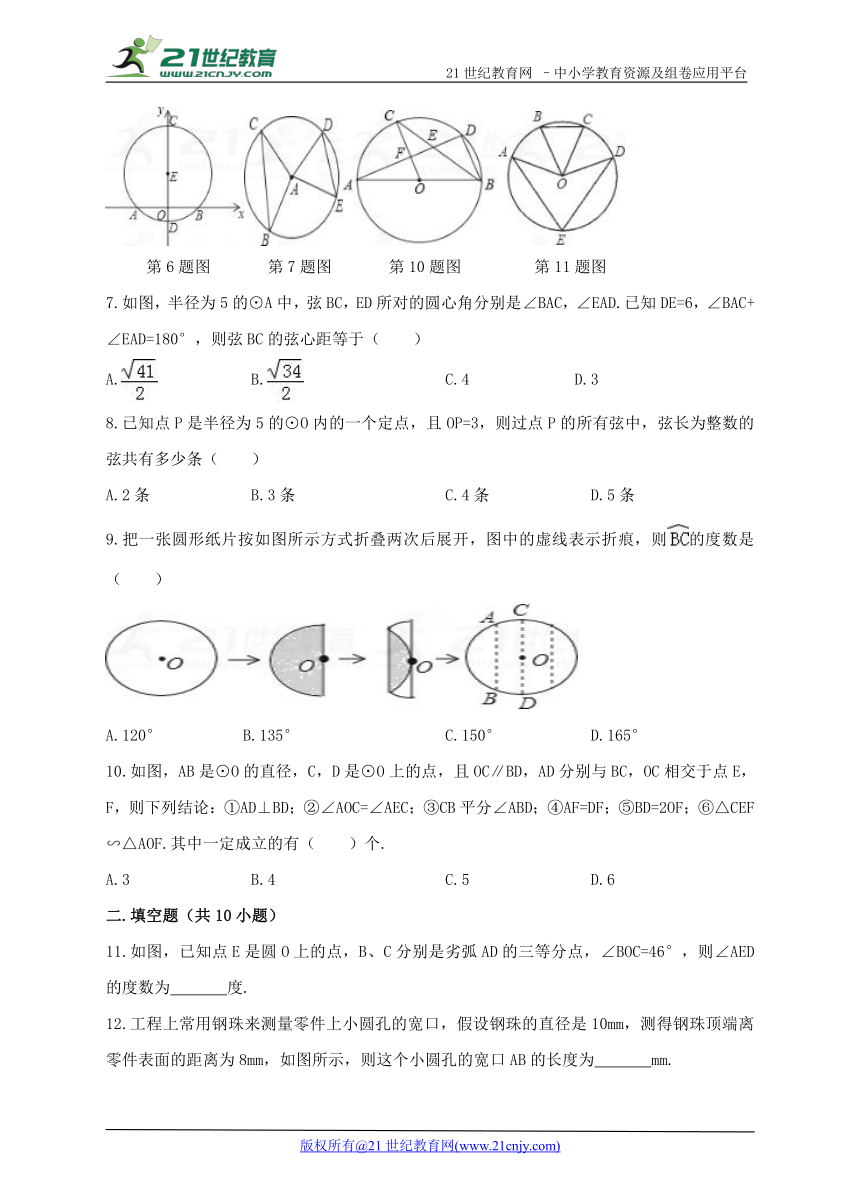
第6题图 第7题图 第10题图 第11题图
7.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )21*cnjy*com
A. B. C.4 D.3
8.已知点P是半径为5的⊙O内的一个定点,且OP=3,则过点P的所有弦中,弦长为整数的弦共有多少条( )【来源:21cnj*y.co*m】
A.2条 B.3条 C.4条 D.5条
9.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120° B.135° C.150° D.165°
10.如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF∽△AOF.其中一定成立的有( )个.21·世纪*教育网
A.3 B.4 C.5 D.6
二.填空题(共10小题)
11.如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为 度.21教育名师原创作品
12.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
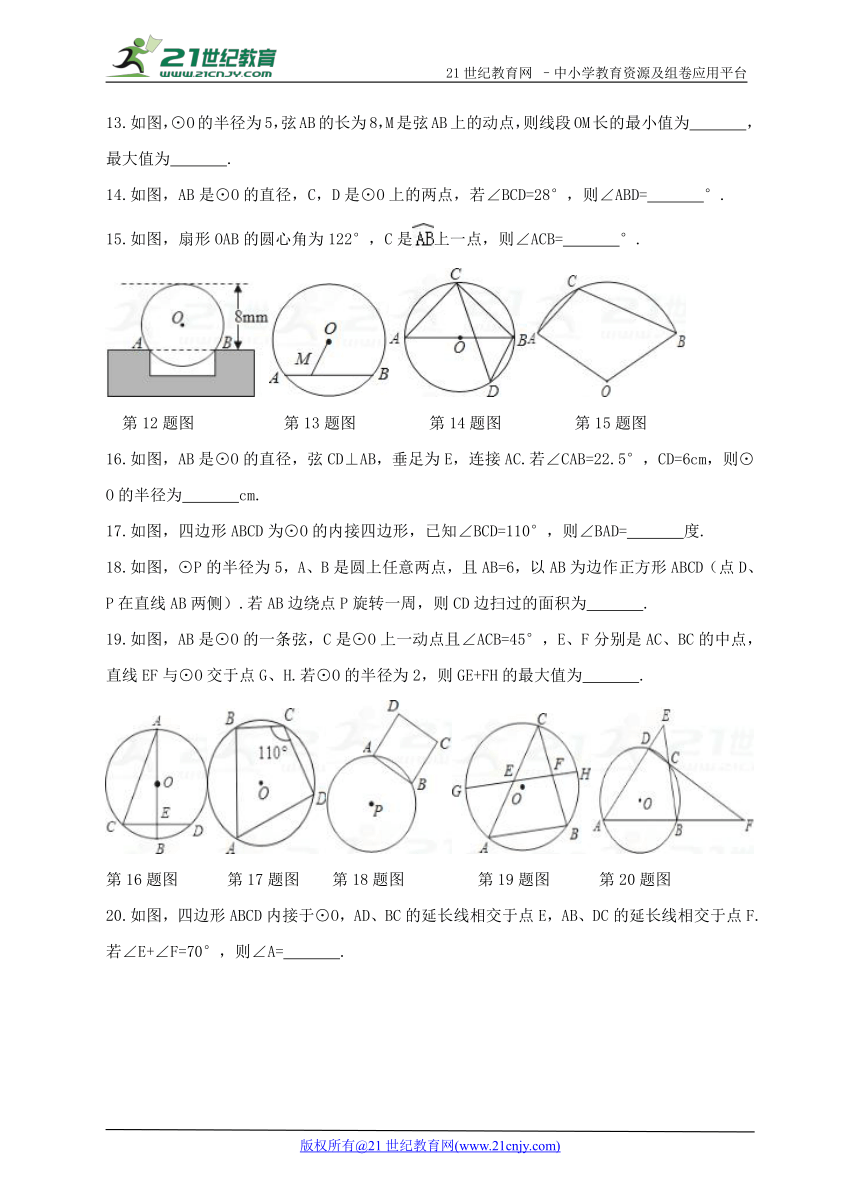
13.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为 ,最大值为 .21*cnjy*com
14.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD= °.
15.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB= °.
第12题图 第13题图 第14题图 第15题图
16.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为 cm.
17.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD= 度.
18.如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为 .
19.如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E、F分别是AC、BC的中点,直线EF与⊙O交于点G、H.若⊙O的半径为2,则GE+FH的最大值为 .
第16题图 第17题图 第18题图 第19题图 第20题图
20.如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A= .【版权所有:21教育】
三.解答题(共6小题)
21.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
22.如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4,AE=2,求圆O的半径.
23.如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.【出处:21教育名师】
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=AD=8,求CD的长.
24.如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.21教育网
25.如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°www-2-1-cnjy-com
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.
26.如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.2-1-c-n-j-y
(1)求证:AE=CK;
(2)如果AB=a,AD=a(a为大于零的常数),求BK的长.
参考答案
一.选择题(共10小题)
1C.【解答】解:如图,连接OC.∵∠BOC=2∠BAC=50°,∠COD=2∠CED=60°,
∴∠BOD=∠BOC+∠COD=110°,故选C.
2A.【解答】解:∵A、B、C是⊙O上的三点,∠B=75°,∴∠AOC=2∠B=150°.故选A.
3B.【解答】解:∵CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,
∴∠DOE=180°﹣40°=140°,∴∠P=∠DOE=70°.故选B.
4D.【解答】解:∵AB是⊙O的直径,∴∠ACB=90°,∵∠B=30°,∴,
∵CE平分∠ACB交⊙O于E,∴=,∴AD=AB,BD=AB,
过C作CF⊥AB于F,连接OE,∵CE平分∠ACB交⊙O于E,∴=,∴OE⊥AB,
∴OE=AB,CF=AB,
∴S△ADE:S△CDB=(AD OE):(BD CF)=():()=2:3.故选D.
方法二:连接BE,易知AE=AB,BC=AB,
由△ADE∽△CDB,∴S△ADE:S△BDC=(AE:BC)2=2:3,故选D.
5C.【解答】解:∵直线y=x﹣3与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,﹣3),3x﹣4y﹣12=0,
即OA=4,OB=3,由勾股定理得:AB=5,
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得:×AB×CM=×OA×OC+×OA×OB,
∴5×CM=4×1+3×4,∴CM=,
∴圆C上点到直线y=x﹣3的最大距离是1+=,
∴△PAB面积的最大值是×5×=,故选:C.
6C.【解答】解:连接EB,如图所示:∵C(0,9),D(0,﹣1),
∴OD=1,OC=9,∴CD=10,∴EB=ED=CD=5,OE=5﹣1=4,∵AB⊥CD,
∴AO=BO=AB,OB===3,∴AB=2OB=6;故选:C.
7D.【解答】解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,∴=,∴DE=BF=6,∵AH⊥BC,∴CH=BH,
而CA=AF,∴AH为△CBF的中位线,∴AH=BF=3.故选:D.
8C.【解答】解:如图,过P作弦AB⊥OP,交⊙O于A、B,连接OA;
Rt△OAP中,OP=3,OA=5;根据勾股定理,得AP=4;∴AB=2AP=8;
故过点P的弦的长度都在8~10之间;
因此弦长为8、9、10;
当弦长为8、10时,过P点的弦分别为弦AB和过P点的直径,分别有一条;
当弦长为9时,根据圆的对称性知,符合条件的弦应该有两条;
故弦长为整数的弦共有4条.故选C.
9C.【解答】解:如图所示:连接BO,过点O作OE⊥AB于点E,
由题意可得:EO=BO,AB∥DC,可得∠EBO=30°,故∠BOD=30°,则∠BOC=150°,
故的度数是150°.故选:C.
10B.【解答】解:①∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,所以选项①正确;
②∵C,D是⊙O上的点,∴与不一定相等,∴∠A与∠CBA不一定相等,
∵OB=OC,∴∠C=∠CBA,∴∠A与∠C不一定相等,∵∠AFO=∠CFE,
∴∠AOC与∠AEC不一定相等,∴△CEF与△AOF不一定相似,所以②和⑥不正确;
③∵OB=OC,∴∠C=∠ABC,∵OC∥BD,∴∠C=∠CBD,∴∠ABC=∠CBD,∴CB平分∠ABD,
所以③正确;
④∵OC∥BD,∴∠AFO=∠ADB=90°,∴OC⊥AD,∴AF=DF,所以④正确;
⑤∵AO=BO,AF=FD,∴OF是△ABD的中位线,∴BD=2OF,所以⑤正确,
所以本题正确的结论有:①③④⑤,一共4个;故选B.
二.填空题(共10小题)
11. 69 度.
【解答】解:∵B、C分别是劣弧AD的三等分点,∠BOC=46°,∴∠AOD=138°,
∴∠AED=138°÷2=69°.
12. 8 mm.
【解答】解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,∵钢珠的直径是10mm,
∴钢珠的半径是5mm,∵钢珠顶端离零件表面的距离为8mm,∴OD=3mm,
在Rt△AOD中,
∵AD===4mm,∴AB=2AD=2×4=8mm.故答案为:8.
13. 3 , 5 .
【解答】解:如图所示,过O作OM′⊥AB,连接OA,
∵过直线外一点与直线上的所有连线中垂线段最短,
∴当OM于OM′重合时OM最短,∵AB=8,OA=5,∴AM′=×8=4,
∴在Rt△OAM′中,OM′===3,
∴线段OM长的最小值为3,最大值为5.
故答案为:3,5.
14. 62 °.
【解答】解:∵AB是⊙O的直径,∴∠ACB=90°,∵∠BCD=28°,∴∠ACD=62°,
由圆周角定理得,∠ABD=∠ACD=62°,故答案为:62.
15. 119 °.
【解答】解:如图所示,在⊙O上取点D,连接AD,BD,∵∠AOB=122°,
∴∠ADB=∠AOB=×122°=61°.∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣61°=119°.故答案为:119.
16. 3 cm.
【解答】解:连接OC,如图所示:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE=CD=3cm,∵OA=OC,∴∠A=∠OCA=22.5°,∵∠COE为△AOC的外角,∴∠COE=45°,
∴△COE为等腰直角三角形,∴OC=CE=3cm,故答案为:3.
17. 70 度.
【解答】解:∵四边形ABCD为⊙O的内接四边形,
∴∠BCD+∠BAD=180°(圆内接四边形的对角互补);又∵∠BCD=110°,
∴∠BAD=70°.故答案为:70.
18. 9π .
【解答】解:连接PD,过点P作PE⊥CD与点E,PE交AB于点F,则CD边扫过的面积为以PD为外圆半径、PE为内圆半径的圆环面积,如图所示.21世纪教育网版权所有
∵PE⊥CD,AB∥CD,∴PF⊥AB.又∵AB为⊙P的弦,∴AF=BF,∴DE=CE=CD=AB=3,
∴CD边扫过的面积为π(PD2﹣PE2)=π DE2=9π.故答案为:9π.
19. 4﹣ .
【解答】解:连接OA,OB,∵∠ACB=45°,∴∠AOB=90°.∵OA=OB,
∴△AOB是等腰直角三角形,∴AB=2,
当GH为⊙O的直径时,GE+FH有最大值.∵点E、F分别为AC、BC的中点,
∴EF=AB=,∴GE+FH=GH﹣EF=4﹣,故答案为:4﹣.
20. 55° .
【解答】解:∵四边形ABCD内接于⊙O,∴∠ADC=∠FBC,
∵∠ADC=180°﹣∠A﹣∠F,∠FBC=∠A+∠E,∴180°﹣∠A﹣∠F=∠A+∠E,
则2∠A=180°﹣(∠F+∠E)=110°,解得,∠A=55°,故答案为:55°.
三.解答题(共6小题)
21.【解答】(1)证明:∵ED=EC,∴∠EDC=∠C,
∵∠EDC=∠B,(∵∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,∴AB=AC;
(2)方法一:
解:连接AE,∵AB为直径,∴AE⊥BC,由(1)知AB=AC,∴BE=CE=BC=,
∵△CDE∽△CBA,∴,∴CE CB=CD CA,AC=AB=4,
∴ 2=4CD,∴CD=.
方法二:解:连接BD,∵AB为直径,∴BD⊥AC,
设CD=a,由(1)知AC=AB=4,则AD=4﹣a,
在Rt△ABD中,由勾股定理可得:BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理可得:BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2整理得:a=,即:CD=.
22.【解答】解:(1)∵CD⊥AB,∠A=48°,∴∠ADE=42°.∴∠AOC=2∠ADE=84°,
∴∠OCE=90°﹣84°=6°;
(2)解:因为AB是圆O的直径,且CD⊥AB于点E,所以CE=CE=×4=2,
在Rt△OCE中,OC2=CE2+OE2,
设圆O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,所以r2=(2)2+(r﹣2)2,
解得:r=3.所以圆O的半径为3.
23.【解答】(1)证明:∵AD是直径,∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD,
∴∠BAD=∠CAD,∵AB=AC,∴BE=CE;
(2)四边形BFCD是菱形.理由如下:
证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中,,∴△BED≌△CEF,∴CF=BD,
∴四边形BFCD是平行四边形,∵∠BAD=∠CAD,∴BD=CD,∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∴CE2=DE AE,设DE=x,∵BC=8,AD=10,∴42=x(10﹣x),解得:x=4,
在Rt△CED中,CD==4.
24.【解答】解:(1)连接OA,根据题意得:CD=4米,AB=12米,则AD=AB=6(米),
设这座拱桥所在圆的半径为x米,则OA=OC=x米,OD=OC﹣CD=(x﹣4)米,
在Rt△AOD中,OA2=OD2+AD2,则x2=(x﹣4)2+62,解得:x=6.5,
故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:连接OM,设MN=5米,∵OC⊥MN,∴MH=MN=2.5(米),
在Rt△OMH中,OH==6(米),∵OD=OC﹣CD=6.5﹣4=2.5(米)
∵OH﹣OD=6﹣2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.
25.【解答】解:(1)∵=,∴∠ACB=∠ADB=45°,∵∠ABD=45°,∴∠BAD=90°,
∴BD是△ABD外接圆的直径;
(2)在CD的延长线上截取DE=BC,连接EA,∵∠ABD=∠ADB,∴AB=AD,
∵∠ADE+∠ADC=180°,∠ABC+∠ADC=180°,∴∠ABC=∠ADE,
在△ABC与△ADE中,,∴△ABC≌△ADE(SAS),∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE=90°,∵=∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,∴AC=CE,∴AC=CD+DE=CD+BC;
(3)过点M作MF⊥MB于点M,过点A作AF⊥MA于点A,MF与AF交于点F,连接BF,
由对称性可知:∠AMB=∠ACB=45°,
∴∠FMA=45°,
∴△AMF是等腰直角三角形,∴AM=AF,MF=AM,
∵∠MAF+∠MAB=∠BAD+∠MAB,∴∠FAB=∠MAD,
在△ABF与△ADM中,,∴△ABF≌△ADM(SAS),
∴BF=DM,在Rt△BMF中,∵BM2+MF2=BF2,∴BM2+2AM2=DM2.
26.【解答】(1)∵DH∥KB,BK⊥AC,∴DE⊥AC,∴∠AED=90°,
∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴∠EAD=∠KCB,
在△ADE和△CBK中∴Rt△ADE≌Rt△CBK,∴AE=CK.
(2)在Rt△ABC中,AB=a,AD=BC=a,
∴AC===,
∵S△ABC=AB×BC=AC×BK,∴BK===a.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
九上数学培优提高 第二十四章 圆 第一节 圆的有关性质
一.选择题(共10小题)
1.如图,⊙O中∠BAC=25°,∠CED=30°,则∠BOD的度数是( )
A.150° B.125° C.110° D.55°
2.如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
A.150° B.140° C.130° D.120°
3.如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )21cnjy.com
A.140° B.70° C.60° D.40°21·cn·jy·com
第1题图 第2题图 第3题图 第4题图 第5题图
4.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )www.21-cn-jy.com
A.1: B.1: C.1:2 D.2:3
5.如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.8 B.12 C. D.
6.如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,9),D(0,﹣1),则线段AB的长度为( )2·1·c·n·j·y
A.3 B.4 C.6 D.8【来源:21·世纪·教育·网】
第6题图 第7题图 第10题图 第11题图
7.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )21*cnjy*com
A. B. C.4 D.3
8.已知点P是半径为5的⊙O内的一个定点,且OP=3,则过点P的所有弦中,弦长为整数的弦共有多少条( )【来源:21cnj*y.co*m】
A.2条 B.3条 C.4条 D.5条
9.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是( )
A.120° B.135° C.150° D.165°
10.如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF∽△AOF.其中一定成立的有( )个.21·世纪*教育网
A.3 B.4 C.5 D.6
二.填空题(共10小题)
11.如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为 度.21教育名师原创作品
12.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
13.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为 ,最大值为 .21*cnjy*com
14.如图,AB是⊙O的直径,C,D是⊙O上的两点,若∠BCD=28°,则∠ABD= °.
15.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB= °.
第12题图 第13题图 第14题图 第15题图
16.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为 cm.
17.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD= 度.
18.如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为 .
19.如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E、F分别是AC、BC的中点,直线EF与⊙O交于点G、H.若⊙O的半径为2,则GE+FH的最大值为 .
第16题图 第17题图 第18题图 第19题图 第20题图
20.如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=70°,则∠A= .【版权所有:21教育】
三.解答题(共6小题)
21.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2,求CD的长.
22.如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4,AE=2,求圆O的半径.
23.如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.【出处:21教育名师】
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=AD=8,求CD的长.
24.如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.21教育网
25.如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°www-2-1-cnjy-com
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.
26.如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.2-1-c-n-j-y
(1)求证:AE=CK;
(2)如果AB=a,AD=a(a为大于零的常数),求BK的长.
参考答案
一.选择题(共10小题)
1C.【解答】解:如图,连接OC.∵∠BOC=2∠BAC=50°,∠COD=2∠CED=60°,
∴∠BOD=∠BOC+∠COD=110°,故选C.
2A.【解答】解:∵A、B、C是⊙O上的三点,∠B=75°,∴∠AOC=2∠B=150°.故选A.
3B.【解答】解:∵CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,
∴∠DOE=180°﹣40°=140°,∴∠P=∠DOE=70°.故选B.
4D.【解答】解:∵AB是⊙O的直径,∴∠ACB=90°,∵∠B=30°,∴,
∵CE平分∠ACB交⊙O于E,∴=,∴AD=AB,BD=AB,
过C作CF⊥AB于F,连接OE,∵CE平分∠ACB交⊙O于E,∴=,∴OE⊥AB,
∴OE=AB,CF=AB,
∴S△ADE:S△CDB=(AD OE):(BD CF)=():()=2:3.故选D.
方法二:连接BE,易知AE=AB,BC=AB,
由△ADE∽△CDB,∴S△ADE:S△BDC=(AE:BC)2=2:3,故选D.
5C.【解答】解:∵直线y=x﹣3与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,﹣3),3x﹣4y﹣12=0,
即OA=4,OB=3,由勾股定理得:AB=5,
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得:×AB×CM=×OA×OC+×OA×OB,
∴5×CM=4×1+3×4,∴CM=,
∴圆C上点到直线y=x﹣3的最大距离是1+=,
∴△PAB面积的最大值是×5×=,故选:C.
6C.【解答】解:连接EB,如图所示:∵C(0,9),D(0,﹣1),
∴OD=1,OC=9,∴CD=10,∴EB=ED=CD=5,OE=5﹣1=4,∵AB⊥CD,
∴AO=BO=AB,OB===3,∴AB=2OB=6;故选:C.
7D.【解答】解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,∴=,∴DE=BF=6,∵AH⊥BC,∴CH=BH,
而CA=AF,∴AH为△CBF的中位线,∴AH=BF=3.故选:D.
8C.【解答】解:如图,过P作弦AB⊥OP,交⊙O于A、B,连接OA;
Rt△OAP中,OP=3,OA=5;根据勾股定理,得AP=4;∴AB=2AP=8;
故过点P的弦的长度都在8~10之间;
因此弦长为8、9、10;
当弦长为8、10时,过P点的弦分别为弦AB和过P点的直径,分别有一条;
当弦长为9时,根据圆的对称性知,符合条件的弦应该有两条;
故弦长为整数的弦共有4条.故选C.
9C.【解答】解:如图所示:连接BO,过点O作OE⊥AB于点E,
由题意可得:EO=BO,AB∥DC,可得∠EBO=30°,故∠BOD=30°,则∠BOC=150°,
故的度数是150°.故选:C.
10B.【解答】解:①∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,所以选项①正确;
②∵C,D是⊙O上的点,∴与不一定相等,∴∠A与∠CBA不一定相等,
∵OB=OC,∴∠C=∠CBA,∴∠A与∠C不一定相等,∵∠AFO=∠CFE,
∴∠AOC与∠AEC不一定相等,∴△CEF与△AOF不一定相似,所以②和⑥不正确;
③∵OB=OC,∴∠C=∠ABC,∵OC∥BD,∴∠C=∠CBD,∴∠ABC=∠CBD,∴CB平分∠ABD,
所以③正确;
④∵OC∥BD,∴∠AFO=∠ADB=90°,∴OC⊥AD,∴AF=DF,所以④正确;
⑤∵AO=BO,AF=FD,∴OF是△ABD的中位线,∴BD=2OF,所以⑤正确,
所以本题正确的结论有:①③④⑤,一共4个;故选B.
二.填空题(共10小题)
11. 69 度.
【解答】解:∵B、C分别是劣弧AD的三等分点,∠BOC=46°,∴∠AOD=138°,
∴∠AED=138°÷2=69°.
12. 8 mm.
【解答】解:连接OA,过点O作OD⊥AB于点D,则AB=2AD,∵钢珠的直径是10mm,
∴钢珠的半径是5mm,∵钢珠顶端离零件表面的距离为8mm,∴OD=3mm,
在Rt△AOD中,
∵AD===4mm,∴AB=2AD=2×4=8mm.故答案为:8.
13. 3 , 5 .
【解答】解:如图所示,过O作OM′⊥AB,连接OA,
∵过直线外一点与直线上的所有连线中垂线段最短,
∴当OM于OM′重合时OM最短,∵AB=8,OA=5,∴AM′=×8=4,
∴在Rt△OAM′中,OM′===3,
∴线段OM长的最小值为3,最大值为5.
故答案为:3,5.
14. 62 °.
【解答】解:∵AB是⊙O的直径,∴∠ACB=90°,∵∠BCD=28°,∴∠ACD=62°,
由圆周角定理得,∠ABD=∠ACD=62°,故答案为:62.
15. 119 °.
【解答】解:如图所示,在⊙O上取点D,连接AD,BD,∵∠AOB=122°,
∴∠ADB=∠AOB=×122°=61°.∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣61°=119°.故答案为:119.
16. 3 cm.
【解答】解:连接OC,如图所示:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE=CD=3cm,∵OA=OC,∴∠A=∠OCA=22.5°,∵∠COE为△AOC的外角,∴∠COE=45°,
∴△COE为等腰直角三角形,∴OC=CE=3cm,故答案为:3.
17. 70 度.
【解答】解:∵四边形ABCD为⊙O的内接四边形,
∴∠BCD+∠BAD=180°(圆内接四边形的对角互补);又∵∠BCD=110°,
∴∠BAD=70°.故答案为:70.
18. 9π .
【解答】解:连接PD,过点P作PE⊥CD与点E,PE交AB于点F,则CD边扫过的面积为以PD为外圆半径、PE为内圆半径的圆环面积,如图所示.21世纪教育网版权所有
∵PE⊥CD,AB∥CD,∴PF⊥AB.又∵AB为⊙P的弦,∴AF=BF,∴DE=CE=CD=AB=3,
∴CD边扫过的面积为π(PD2﹣PE2)=π DE2=9π.故答案为:9π.
19. 4﹣ .
【解答】解:连接OA,OB,∵∠ACB=45°,∴∠AOB=90°.∵OA=OB,
∴△AOB是等腰直角三角形,∴AB=2,
当GH为⊙O的直径时,GE+FH有最大值.∵点E、F分别为AC、BC的中点,
∴EF=AB=,∴GE+FH=GH﹣EF=4﹣,故答案为:4﹣.
20. 55° .
【解答】解:∵四边形ABCD内接于⊙O,∴∠ADC=∠FBC,
∵∠ADC=180°﹣∠A﹣∠F,∠FBC=∠A+∠E,∴180°﹣∠A﹣∠F=∠A+∠E,
则2∠A=180°﹣(∠F+∠E)=110°,解得,∠A=55°,故答案为:55°.
三.解答题(共6小题)
21.【解答】(1)证明:∵ED=EC,∴∠EDC=∠C,
∵∠EDC=∠B,(∵∠EDC+∠ADE=180°,∠B+∠ADE=180°,∴∠EDC=∠B)
∴∠B=∠C,∴AB=AC;
(2)方法一:
解:连接AE,∵AB为直径,∴AE⊥BC,由(1)知AB=AC,∴BE=CE=BC=,
∵△CDE∽△CBA,∴,∴CE CB=CD CA,AC=AB=4,
∴ 2=4CD,∴CD=.
方法二:解:连接BD,∵AB为直径,∴BD⊥AC,
设CD=a,由(1)知AC=AB=4,则AD=4﹣a,
在Rt△ABD中,由勾股定理可得:BD2=AB2﹣AD2=42﹣(4﹣a)2
在Rt△CBD中,由勾股定理可得:BD2=BC2﹣CD2=(2)2﹣a2
∴42﹣(4﹣a)2=(2)2﹣a2整理得:a=,即:CD=.
22.【解答】解:(1)∵CD⊥AB,∠A=48°,∴∠ADE=42°.∴∠AOC=2∠ADE=84°,
∴∠OCE=90°﹣84°=6°;
(2)解:因为AB是圆O的直径,且CD⊥AB于点E,所以CE=CE=×4=2,
在Rt△OCE中,OC2=CE2+OE2,
设圆O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,所以r2=(2)2+(r﹣2)2,
解得:r=3.所以圆O的半径为3.
23.【解答】(1)证明:∵AD是直径,∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,,∴Rt△ABD≌Rt△ACD,
∴∠BAD=∠CAD,∵AB=AC,∴BE=CE;
(2)四边形BFCD是菱形.理由如下:
证明:∵AD是直径,AB=AC,∴AD⊥BC,BE=CE,∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中,,∴△BED≌△CEF,∴CF=BD,
∴四边形BFCD是平行四边形,∵∠BAD=∠CAD,∴BD=CD,∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∴CE2=DE AE,设DE=x,∵BC=8,AD=10,∴42=x(10﹣x),解得:x=4,
在Rt△CED中,CD==4.
24.【解答】解:(1)连接OA,根据题意得:CD=4米,AB=12米,则AD=AB=6(米),
设这座拱桥所在圆的半径为x米,则OA=OC=x米,OD=OC﹣CD=(x﹣4)米,
在Rt△AOD中,OA2=OD2+AD2,则x2=(x﹣4)2+62,解得:x=6.5,
故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:连接OM,设MN=5米,∵OC⊥MN,∴MH=MN=2.5(米),
在Rt△OMH中,OH==6(米),∵OD=OC﹣CD=6.5﹣4=2.5(米)
∵OH﹣OD=6﹣2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.
25.【解答】解:(1)∵=,∴∠ACB=∠ADB=45°,∵∠ABD=45°,∴∠BAD=90°,
∴BD是△ABD外接圆的直径;
(2)在CD的延长线上截取DE=BC,连接EA,∵∠ABD=∠ADB,∴AB=AD,
∵∠ADE+∠ADC=180°,∠ABC+∠ADC=180°,∴∠ABC=∠ADE,
在△ABC与△ADE中,,∴△ABC≌△ADE(SAS),∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE=90°,∵=∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,∴AC=CE,∴AC=CD+DE=CD+BC;
(3)过点M作MF⊥MB于点M,过点A作AF⊥MA于点A,MF与AF交于点F,连接BF,
由对称性可知:∠AMB=∠ACB=45°,
∴∠FMA=45°,
∴△AMF是等腰直角三角形,∴AM=AF,MF=AM,
∵∠MAF+∠MAB=∠BAD+∠MAB,∴∠FAB=∠MAD,
在△ABF与△ADM中,,∴△ABF≌△ADM(SAS),
∴BF=DM,在Rt△BMF中,∵BM2+MF2=BF2,∴BM2+2AM2=DM2.
26.【解答】(1)∵DH∥KB,BK⊥AC,∴DE⊥AC,∴∠AED=90°,
∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴∠EAD=∠KCB,
在△ADE和△CBK中∴Rt△ADE≌Rt△CBK,∴AE=CK.
(2)在Rt△ABC中,AB=a,AD=BC=a,
∴AC===,
∵S△ABC=AB×BC=AC×BK,∴BK===a.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
