24.2 点、圆、线和圆的位置关系培优提高试题
文档属性
| 名称 | 24.2 点、圆、线和圆的位置关系培优提高试题 |

|
|
| 格式 | doc | ||
| 文件大小 | 839.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-23 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
九上数学培优提高 第二十四章第2节 点、圆、线和圆的位置关系
一.选择题(共10小题)
1.已知⊙O1与⊙O2半径的长是x2﹣7x+12=0的两根,且O1O2=6,则两圆的位置关系是( )
A.相交 B.内切 C.内含 D.外切
2.如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )
A.4cm B.2cm C.2cm D.m
3.下列直线中,一定是圆的切线的是( )
A.与圆有公共点的直线 B.垂直于圆的半径的直线
C.到圆心的距离等于半径的直线 D.经过圆的直径一端的直线
4.如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=40°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )21·cn·jy·com
A.50° B.55° C.65° D.70°
5.如图,在平面直角坐标系中,点A、B均在函数y=(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )2·1·c·n·j·y
A.(2,2) B.(2,3) C.(3,2) D.(4,)
6.在△ABC中,∠C=90°,AC=BC=4cm,D是AB的中点,以C为圆心,4cm长为半径作圆,则A,B,C,D四点中,在圆内的有( )【来源:21·世纪·教育·网】
A.4个 B.3个 C.2个 D.1个
7.如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,﹣4),则圆心M的坐标为( )
A. (﹣2,2.5) B.(2,﹣1.5) C.(2.5,﹣2) D.(2,﹣2.5)
第2题图 第4题图 第5题图 第7题图
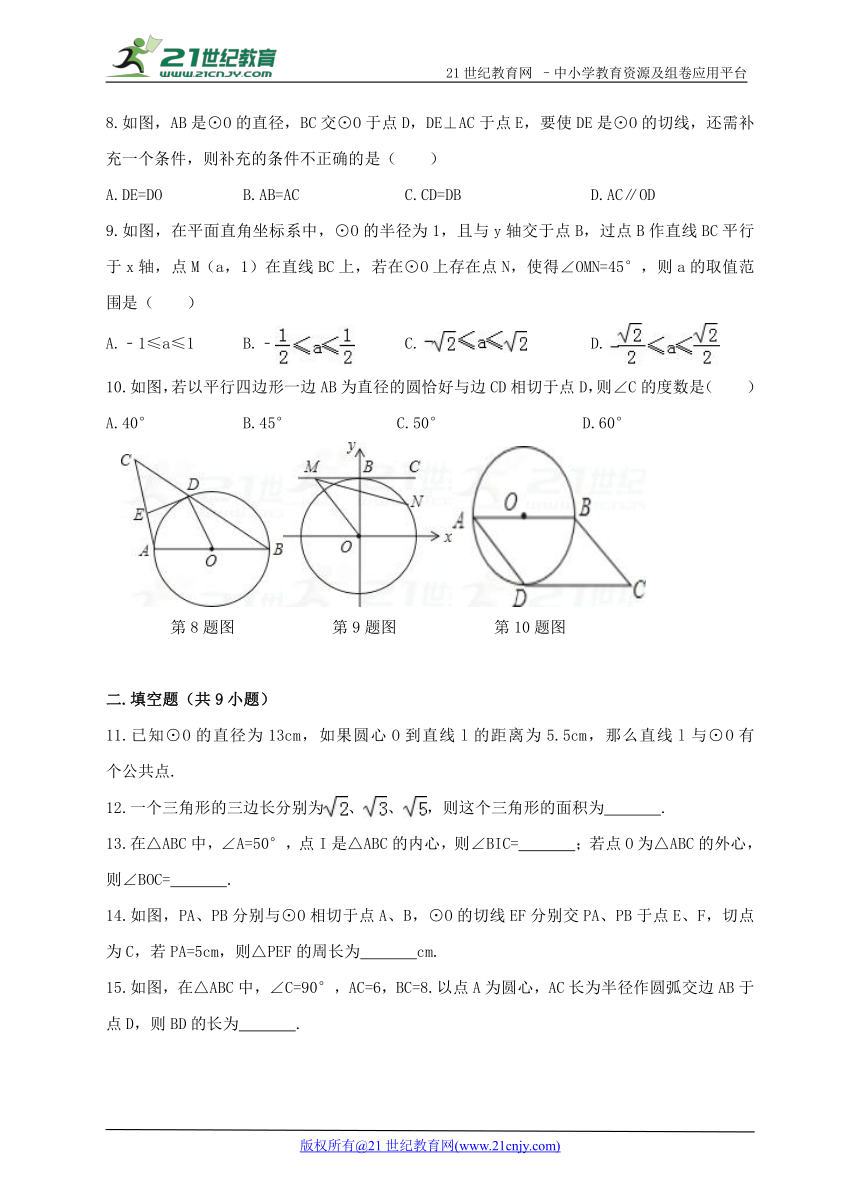
8.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )21·世纪*教育网
A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
9.如图,在平面直角坐标系中,⊙O的半径为1,且与y轴交于点B,过点B作直线BC平行于x轴,点M(a,1)在直线BC上,若在⊙O上存在点N,使得∠OMN=45°,则a的取值范围是( )www-2-1-cnjy-com
A.﹣1≤a≤1 B.﹣ C. D.
10.如图,若以平行四边形一边AB为直径的圆恰好与边CD相切于点D,则∠C的度数是( )
A.40° B.45° C.50° D.60°
第8题图 第9题图 第10题图
二.填空题(共9小题)
11.已知⊙O的直径为13cm,如果圆心O到直线l的距离为5.5cm,那么直线l与⊙O有 个公共点.21教育网
12.一个三角形的三边长分别为、、,则这个三角形的面积为 .
13.在△ABC中,∠A=50°,点I是△ABC的内心,则∠BIC= ;若点O为△ABC的外心,则∠BOC= .2-1-c-n-j-y
14.如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为 cm.【出处:21教育名师】
15.如图,在△ABC中,∠C=90°,AC=6,BC=8.以点A为圆心,AC长为半径作圆弧交边AB于点D,则BD的长为 .【版权所有:21教育】
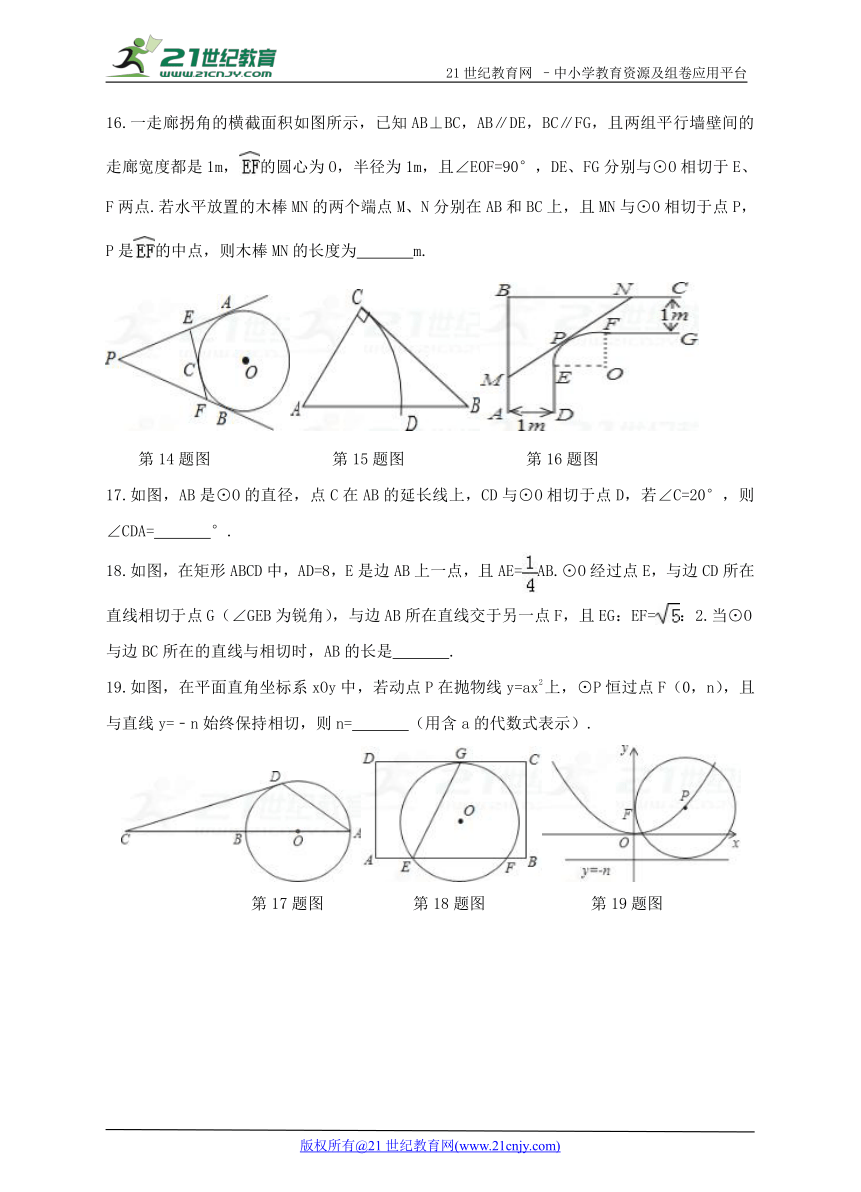
16.一走廊拐角的横截面积如图所示,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m,的圆心为O,半径为1m,且∠EOF=90°,DE、FG分别与⊙O相切于E、F两点.若水平放置的木棒MN的两个端点M、N分别在AB和BC上,且MN与⊙O相切于点P,P是的中点,则木棒MN的长度为 m.21教育名师原创作品
第14题图 第15题图 第16题图
17.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.www.21-cn-jy.com
18.如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=:2.当⊙O与边BC所在的直线与相切时,AB的长是 .21*cnjy*com
19.如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,n),且与直线y=﹣n始终保持相切,则n= (用含a的代数式表示).
第17题图 第18题图 第19题图
三.解答题(共6小题)
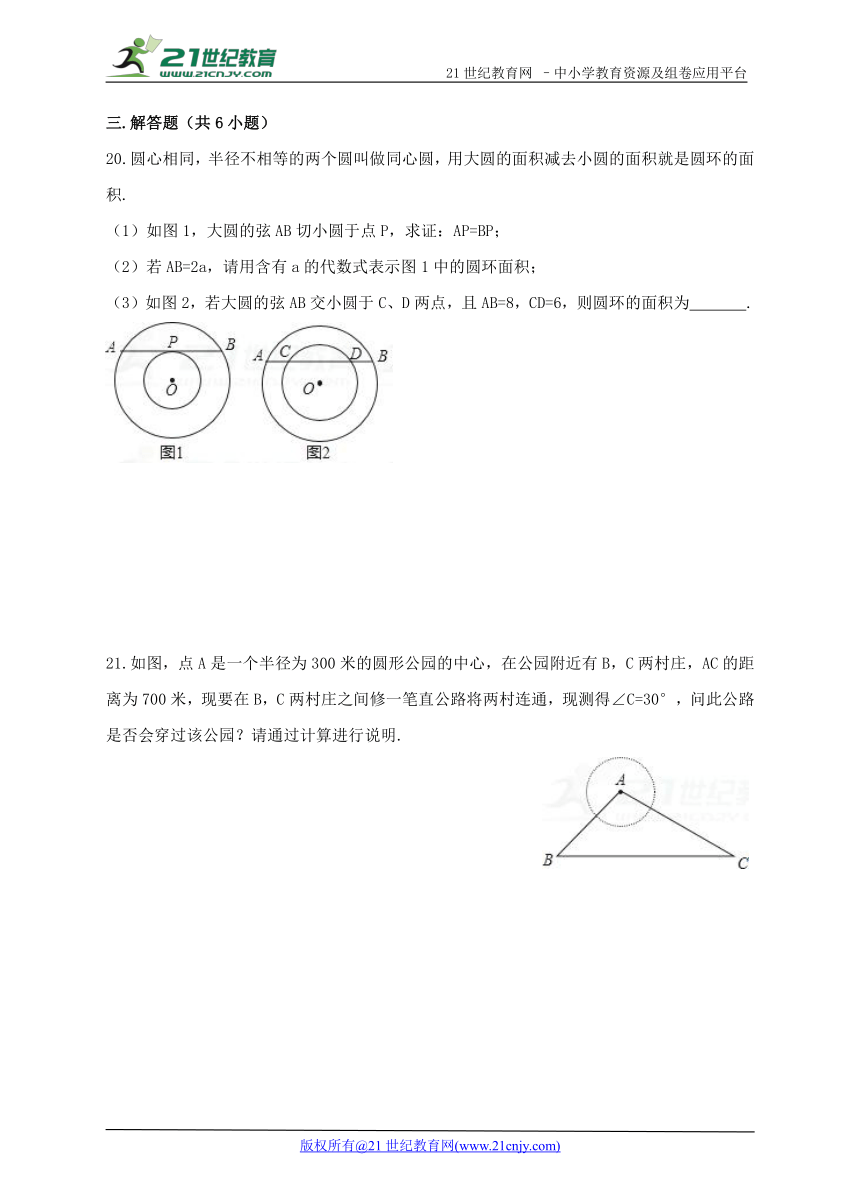
20.圆心相同,半径不相等的两个圆叫做同心圆,用大圆的面积减去小圆的面积就是圆环的面积.
(1)如图1,大圆的弦AB切小圆于点P,求证:AP=BP;
(2)若AB=2a,请用含有a的代数式表示图1中的圆环面积;
(3)如图2,若大圆的弦AB交小圆于C、D两点,且AB=8,CD=6,则圆环的面积为 .
21.如图,点A是一个半径为300米的圆形公园的中心,在公园附近有B,C两村庄,AC的距离为700米,现要在B,C两村庄之间修一笔直公路将两村连通,现测得∠C=30°,问此公路是否会穿过该公园?请通过计算进行说明.21cnjy.com
22.如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.21*cnjy*com
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
23.如图,已知点E是矩形ABCD的边AB上一点,BE:EA=5:3,EC=,把△BEC沿折痕EC向上翻折,若点B恰好在AD上,设这个点为F.【来源:21cnj*y.co*m】
(1)求AB、BC的长度各是多少?
(2)若⊙O内切于以F、E、B、C为顶点的四边形,求⊙O的面积.
24.如图,已知:AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.
(1)如图1,若∠CPA=30°,求∠CDP的度数;
(2)如图2,若∠CPA≠30°,(1)中的结论是否依然成立?若成立,请说明理由;若不成立,请求出∠CDP的度数.
25.如图,在平面直角坐标系中,四边形OADC是矩形,OA=6,AB=4,直线y=﹣x+3与坐标轴交于D,E.设M是AB的中点,P是线段DE上的动点,
(1)求M、D两点的坐标;
(2)当P在什么位置时,PA=PB求出此时P点的坐标;
(3)过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,求梯形PMBH的面积.
九上数学培优提高 第二十四章第2节 点、圆、线和圆的位置关系
参考答案与试题解析
一.选择题(共10小题)
1A.【解答】解:解方程x2﹣7x+12=0得x1=3,x2=4,∵O1O2=6,x2﹣x1=1,
∴x2﹣x1<O1O2<x2+x1,∴⊙O1与⊙O2相交.故选A.
2A.【解答】解:连接OB,如图,∵AB与⊙O切于点B,∴OB⊥AB,∴∠ABO=90°,
在Rt△ABO中,∵AO=5,AB=3,∴OB==4,∴⊙O的半径为4cm.故选A.
3C.【解答】解:A、与圆有1个公共点的直线是圆的切线,与圆有2个公共点的直线是圆的割线;故本选项错误;
B、垂直于圆的半径且过此半径的外端点的直线是圆的切线;故本选项错误;
C、到圆心的距离等于半径的直线是圆的切线;故本选项正确;
D、经过圆的直径一端且的直线且垂直于此直径的直线是圆的切线;故本选项错误.
故选C.
4A.【解答】解:∵∠A+∠B+∠C=180°,∠B=40°,∠C=60°,∴∠A=80°,
∵⊙O内切于△ABC,切点分别为D、E、F,∴∠OEA=∠OFA=90°,
∴∠EOF=360°﹣∠A﹣∠OEA﹣∠OFA=100°,∴∠EDF=∠EOF=50°.故选A.
5C.【解答】解:把B的坐标为(1,6)代入反比例函数解析式得:k=6,
则函数的解析式是:y=,∵B的坐标为(1,6),⊙B与y轴相切,
∴⊙B的半径是1,则⊙A是2,把y=2代入y=得:x=3,则A的坐标是(3,2).
故选:C.
6C.【解答】解:∵以C为圆心,4cm长为半径作圆,∠C=90°,AC=BC=4cm,
则A、B到圆心C的距离等于半径,∴点A、B在圆上;
又∵在直角三角形ABC中,D是AB的中点,AC=BC=4cm,则AB==4,
∴CD=AB=2,则2<4,∴点D在⊙C内,那么在圆内只有点C和点D两个点.故选C.
7D.【解答】解:∵四边形ABCO是正方形,A(0,﹣4),∴AB=OA=CO=BC=4,
过M作MN⊥AB于N,连接MA,由垂径定理得:AN=AB=2,
设⊙M的半径是R,则MN=8﹣R,AM=R,由勾股定理得:AM2=MN2+AN2,
R2=(4﹣R)2+22,解得:R=,∵AN=2,四边形ABCO是正方形,⊙M于x轴相切,
∴M的横坐标是2,即M(2,﹣).故选D.
8A.【解答】解:当AB=AC时,如图:连接AD,∵AB是⊙O的直径,∴AD⊥BC,∴CD=BD,
∵AO=BO,∴OD是△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,∴DE是⊙O的切线.
所以B正确.当CD=BD时,AO=BO,∴OD是△ABC的中位线,∴OD∥AC∵DE⊥AC
∴DE⊥OD∴DE是⊙O的切线.所以C正确.当AC∥OD时,∵DE⊥AC,∴DE⊥OD.
∴DE是⊙O的切线.所以D正确.故选A.
9A.【解答】解:∵点M(a,1)在直线BC上,∴OB=1,∵BC∥x轴,∴BC⊥y轴,∴∠OBM=90°,
当BM=OB=1时,△OBM是等腰直角三角形,则∠OMN=45°,此时a=±1;
当BM>OB时,∠OMN<45°,∴a的取值范围是﹣1≤a≤1;故选:A.
10B.【解答】解:连接OD,如图,∵CD为切线,∴OD⊥CD,∵四边形ABCD为平行四边形,
∴∠A=∠C,AB∥CD,∴OD⊥AB,∴∠BOD=90°,∴∠A=∠BOD=45°,∴∠C=45°.
故选B.
二.填空题(共9小题)
11. 2 .
【解答】解:已知圆的直径为13cm,则半径为6.5cm,又圆心距为5.5cm,小于半径,
所以,直线与圆相交,有两个交点.故答案为:2.
12. .
【解答】解:∵()2+()2=2+3=5,()2=5,
∴()2+()2=()2,∴三角形是直角三角形,
∴这个三角形的面积=××=.故答案为:.
13. 115° ; 100° .
【解答】解:∵∠A+∠ABC+∠ACB=180°,∠A=50°,∴∠ABC+∠ACB=130°,
∵I是△ABC的内心,∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=×130°=65°,∴∠BIC=180°﹣(∠IBC+∠ICB)=115°;
当是图1时,由圆周角定理得:∠BOC=2∠A=2×50°=100°;
当是图2时,同样由圆周角定理得:∠BOC=2∠A=100°;
故答案为:115°,100°
14. 10 cm.
【解答】解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=5,
∴△PEF的周长=PE+EF+PF=PA+PB=10cm,故答案为10
15 4 .
【解答】解:∵AC=6,BC=8,∴AB==10,
∵以点A为圆心,AC长为半径画弧,交AB于点D,∴AD=AC,∴AD=6,
∴BD=AB﹣AD=10﹣6=4.故答案为:4.
16. (4﹣2) m.
【解答】解:连接OB,延长OF,OE分别交BC于H,交AB于K,
∵DE、FG分别与⊙O相切于E、F两点,∴OE⊥ED,OF⊥FG,∵AB∥DE,BC∥FG,
∴OK⊥AB,OH⊥BC,∵∠EOF=90°,∴四边形BKOH是矩形,
∵两组平行墙壁间的走廊宽度都是1m,⊙O半径为1m,∴OK=OH=2,
∴矩形BKOH是正方形,∴∠BOK=∠BOH=45°,∵P是的中点,∴OB经过P点,
在正方形BKOH中,边长=2,∴OB=2,∵OP=1,∴BP=2﹣1,∵p是MN与⊙O的切点,
∴OB⊥MN,∵OB是正方形BKOH的对角线,∴∠OBK=∠OBH=45°,
在△BPM与△BPN中∴△BPM≌△BPN(ASA)∴MP=NP,∴MN=2BP,
∵BP=2﹣1,∴MN=2(2﹣1)=4﹣2,故答案为:4﹣2
17. 125 °.
【解答】解:连接OD,则∠ODC=90°,∠COD=70°;∵OA=OD,∴∠ODA=∠A=∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°,故答案为:125.
18. 12 .
【解答】解:边BC所在的直线与⊙O相切时,
如图,过点G作GN⊥AB,垂足为N,∴EN=NF,又∵EG:EF=:2,∴EG:EN=:1,
又∵GN=AD=8,∴设EN=x,则GE=x,根据勾股定理得:
(x)2﹣x2=64,解得:x=4,GE=4,
设⊙O的半径为r,由OE2=EN2+ON2
得:r2=16+(8﹣r)2,∴r=5.∴OK=NB=5,∴EB=9,又AE=AB,∴AB=12.
故答案为:12.
19. (用含a的代数式表示).
【解答】解:如图,连接PF.设⊙P与直线y=﹣n相切于点E,连接PE.则PE⊥AE.
∵动点P在抛物线y=ax2上,∴设P(m,am2).
∵⊙P恒过点F(0,n),∴PF=PE,即=am2+n.∴n=.
故答案为:.
三.解答题(共6小题)
20.【解答】(1)证明:如图1中,连接OP.
∵AB是小圆的切线,P是切点,∴OP⊥AB,∴PA=PB.
(2)解:如图1中,连接OB.∵大圆的弦AB是小圆的切线,
∴OP⊥AB,AP=PB,∴OB2﹣OP2=(2a÷2)2=a2,
∵S圆环=S大﹣S小=π OB2﹣π OP2=π (OB2﹣OP2),∴S圆环=πa2.
(3)解:如图2中,连接OA,OC,作OE⊥AB于点E.
在Rt△AOE与Rt△OCE中:OE2=OA2﹣AE2,OE2=OC2﹣CE2,
∴OA2﹣AE2=OC2﹣CE2,∴OA2﹣OC2=AE2﹣CE2,∵AB=8,CD=6,∴AE=EB=4,CE=DE=3,
∴OA2﹣OC2=7,∴圆环的面积为:πOA2﹣πOC2=π(OA2﹣OC2)=7π.故答案为7π.
21.【解答】解:如图所示:过点A作AD⊥BC于点D,
由题意可得:AC=700m,∠C=30°,则AD=AC=350m,∵350>300,
∴此公路不会穿过该公园.
22.【解答】解:(1)连接AC,∵点CD是半圆O的三等分点,
∴==,∴∠DAC=∠CAB,∵OA=OC,∴∠CAB=∠OCA,∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)∴∠OCE+∠E=180°,∵CE⊥AD,
∴∠OCE=90°,∴OC⊥CE,∴CE是⊙O的切线;
(2)四边形AOCD为菱形.理由是:∵=,∴∠DCA=∠CAB,∴CD∥OA,
又∵AE∥OC,∴四边形AOCD是平行四边形,∵OA=OC,∴平行四边形AOCD是菱形.
23.【解答】解:(1)∵四边形ABCD是矩形∴∠A=∠B=∠D=90°,BC=AD,AB=CD,
∴∠AFE+∠AEF=90°∵F在AD上,∠EFC=90°∴∠AFE+∠DFC=90°∴∠AEF=∠DFC
∴△AEF∽△DFC∴.∵BE:EA=5:3设BE=5k,AE=3k∴AB=DC=8k,
由勾股定理得:AF=4k,∴∴DF=6k∴BC=AD=10k
在△EBC中,根据勾股定理得BE2+BC2=EC2
∵CE=15 ,BE=5k,BC=10k
∴∴k=3∴AB=8k=24,BC=10k=30
(2)连接OB,由于⊙O内切于以F、E、B、C为顶点的四边形,则BE=EF,BC=CF;
由BE:EA=5:3,设BE=5x,EA=3x,
则FA=4x,CD=8x,又CF=AD,∴CF2=CD2+DF2,即CF2=(8x)2+(CF﹣4x)2,可得CF=10x,DF=6x,则BC=10x;21世纪教育网版权所有
在Rt△EBC中,EB2+BC2=EC2,即(5x)2+(10x)2=15 2,
解得:x=3,则BE=15,BC=30.
再由S△EBC=S△OEB+S△OBC,则 ×BE×BC=×BE×r+×BC×r,解得:r=10;
则⊙O的面积为πr2=100π.
24.【解答】解:(1)连接OC,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=90°,
∵∠CPA=30°,∴∠COP=60°,∵OA=OC,∴∠A=∠ACO=30°,∵PD平分∠APC,
∴∠APD=15°,∴∠CDP=∠A+∠APD=45°.
(2)成立.∵PC是⊙O的切线,∴∠OCP=90°,∵PD是∠CPA的平分线,∴∠APC=2∠APD,
∵OA=OC,∴∠A=∠ACO,∴∠COP=2∠A,
在Rt△OCP中,∠OCP=90°,∴∠COP+∠OPC=90°,∴2(∠A+∠APD)=90°,
∴∠CDP=∠A+∠APD=45°.所以(1)中结论依然成立.
25.【解答】解:(1)∵四边形OABC是矩形,OA=6,AB=4,M是AB的中点,∴OA=6,AM=BM=2,
∴M(6,2);∵直线y=﹣x+3与坐标轴交于D,E,∴当y=0时,﹣x+3=0,
解得:x=3,∴D(3,0);
(2)∵PA=PB,∴点P在线段AB的中垂线上,∴点P的纵坐标是2,
又∵点P在y=﹣x+3上,∴2=﹣x+3,∴x=1,∴点P的坐标为( 1,2);
(3)设P(x,y),连接PN、MN、NF,如图所示:∵点P在y=﹣x+3上,
∴P(x,﹣x+3),
依题意知:PN⊥MN,FN⊥BC,F是圆心,
∴N是线段HB的中点,HN=NB=,PH=4﹣(﹣x+3)=x+1,BM=2,
∵∠HPN+∠HNP=∠HNP+∠BNM=90°,∴∠HPN=∠BNM,又∵∠PHN=∠B=90°,
∴Rt△PNH∽Rt△NMB,∴,∴,
整理得:x2﹣20x+28=0,
解得:x=10+6(不合题意,舍去),或x=10﹣6,
∴梯形PMBH的面积=(BM+PH) BH=(2+10﹣6+1)(6﹣10+6)=51﹣62.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
九上数学培优提高 第二十四章第2节 点、圆、线和圆的位置关系
一.选择题(共10小题)
1.已知⊙O1与⊙O2半径的长是x2﹣7x+12=0的两根,且O1O2=6,则两圆的位置关系是( )
A.相交 B.内切 C.内含 D.外切
2.如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )
A.4cm B.2cm C.2cm D.m
3.下列直线中,一定是圆的切线的是( )
A.与圆有公共点的直线 B.垂直于圆的半径的直线
C.到圆心的距离等于半径的直线 D.经过圆的直径一端的直线
4.如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=40°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )21·cn·jy·com
A.50° B.55° C.65° D.70°
5.如图,在平面直角坐标系中,点A、B均在函数y=(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )2·1·c·n·j·y
A.(2,2) B.(2,3) C.(3,2) D.(4,)
6.在△ABC中,∠C=90°,AC=BC=4cm,D是AB的中点,以C为圆心,4cm长为半径作圆,则A,B,C,D四点中,在圆内的有( )【来源:21·世纪·教育·网】
A.4个 B.3个 C.2个 D.1个
7.如图,在平面直角坐标系中,正方形ABCO的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切,若点A的坐标为(0,﹣4),则圆心M的坐标为( )
A. (﹣2,2.5) B.(2,﹣1.5) C.(2.5,﹣2) D.(2,﹣2.5)
第2题图 第4题图 第5题图 第7题图
8.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )21·世纪*教育网
A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
9.如图,在平面直角坐标系中,⊙O的半径为1,且与y轴交于点B,过点B作直线BC平行于x轴,点M(a,1)在直线BC上,若在⊙O上存在点N,使得∠OMN=45°,则a的取值范围是( )www-2-1-cnjy-com
A.﹣1≤a≤1 B.﹣ C. D.
10.如图,若以平行四边形一边AB为直径的圆恰好与边CD相切于点D,则∠C的度数是( )
A.40° B.45° C.50° D.60°
第8题图 第9题图 第10题图
二.填空题(共9小题)
11.已知⊙O的直径为13cm,如果圆心O到直线l的距离为5.5cm,那么直线l与⊙O有 个公共点.21教育网
12.一个三角形的三边长分别为、、,则这个三角形的面积为 .
13.在△ABC中,∠A=50°,点I是△ABC的内心,则∠BIC= ;若点O为△ABC的外心,则∠BOC= .2-1-c-n-j-y
14.如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点为C,若PA=5cm,则△PEF的周长为 cm.【出处:21教育名师】
15.如图,在△ABC中,∠C=90°,AC=6,BC=8.以点A为圆心,AC长为半径作圆弧交边AB于点D,则BD的长为 .【版权所有:21教育】
16.一走廊拐角的横截面积如图所示,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m,的圆心为O,半径为1m,且∠EOF=90°,DE、FG分别与⊙O相切于E、F两点.若水平放置的木棒MN的两个端点M、N分别在AB和BC上,且MN与⊙O相切于点P,P是的中点,则木棒MN的长度为 m.21教育名师原创作品
第14题图 第15题图 第16题图
17.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.www.21-cn-jy.com
18.如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=:2.当⊙O与边BC所在的直线与相切时,AB的长是 .21*cnjy*com
19.如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,n),且与直线y=﹣n始终保持相切,则n= (用含a的代数式表示).
第17题图 第18题图 第19题图
三.解答题(共6小题)
20.圆心相同,半径不相等的两个圆叫做同心圆,用大圆的面积减去小圆的面积就是圆环的面积.
(1)如图1,大圆的弦AB切小圆于点P,求证:AP=BP;
(2)若AB=2a,请用含有a的代数式表示图1中的圆环面积;
(3)如图2,若大圆的弦AB交小圆于C、D两点,且AB=8,CD=6,则圆环的面积为 .
21.如图,点A是一个半径为300米的圆形公园的中心,在公园附近有B,C两村庄,AC的距离为700米,现要在B,C两村庄之间修一笔直公路将两村连通,现测得∠C=30°,问此公路是否会穿过该公园?请通过计算进行说明.21cnjy.com
22.如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.21*cnjy*com
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
23.如图,已知点E是矩形ABCD的边AB上一点,BE:EA=5:3,EC=,把△BEC沿折痕EC向上翻折,若点B恰好在AD上,设这个点为F.【来源:21cnj*y.co*m】
(1)求AB、BC的长度各是多少?
(2)若⊙O内切于以F、E、B、C为顶点的四边形,求⊙O的面积.
24.如图,已知:AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.
(1)如图1,若∠CPA=30°,求∠CDP的度数;
(2)如图2,若∠CPA≠30°,(1)中的结论是否依然成立?若成立,请说明理由;若不成立,请求出∠CDP的度数.
25.如图,在平面直角坐标系中,四边形OADC是矩形,OA=6,AB=4,直线y=﹣x+3与坐标轴交于D,E.设M是AB的中点,P是线段DE上的动点,
(1)求M、D两点的坐标;
(2)当P在什么位置时,PA=PB求出此时P点的坐标;
(3)过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,求梯形PMBH的面积.
九上数学培优提高 第二十四章第2节 点、圆、线和圆的位置关系
参考答案与试题解析
一.选择题(共10小题)
1A.【解答】解:解方程x2﹣7x+12=0得x1=3,x2=4,∵O1O2=6,x2﹣x1=1,
∴x2﹣x1<O1O2<x2+x1,∴⊙O1与⊙O2相交.故选A.
2A.【解答】解:连接OB,如图,∵AB与⊙O切于点B,∴OB⊥AB,∴∠ABO=90°,
在Rt△ABO中,∵AO=5,AB=3,∴OB==4,∴⊙O的半径为4cm.故选A.
3C.【解答】解:A、与圆有1个公共点的直线是圆的切线,与圆有2个公共点的直线是圆的割线;故本选项错误;
B、垂直于圆的半径且过此半径的外端点的直线是圆的切线;故本选项错误;
C、到圆心的距离等于半径的直线是圆的切线;故本选项正确;
D、经过圆的直径一端且的直线且垂直于此直径的直线是圆的切线;故本选项错误.
故选C.
4A.【解答】解:∵∠A+∠B+∠C=180°,∠B=40°,∠C=60°,∴∠A=80°,
∵⊙O内切于△ABC,切点分别为D、E、F,∴∠OEA=∠OFA=90°,
∴∠EOF=360°﹣∠A﹣∠OEA﹣∠OFA=100°,∴∠EDF=∠EOF=50°.故选A.
5C.【解答】解:把B的坐标为(1,6)代入反比例函数解析式得:k=6,
则函数的解析式是:y=,∵B的坐标为(1,6),⊙B与y轴相切,
∴⊙B的半径是1,则⊙A是2,把y=2代入y=得:x=3,则A的坐标是(3,2).
故选:C.
6C.【解答】解:∵以C为圆心,4cm长为半径作圆,∠C=90°,AC=BC=4cm,
则A、B到圆心C的距离等于半径,∴点A、B在圆上;
又∵在直角三角形ABC中,D是AB的中点,AC=BC=4cm,则AB==4,
∴CD=AB=2,则2<4,∴点D在⊙C内,那么在圆内只有点C和点D两个点.故选C.
7D.【解答】解:∵四边形ABCO是正方形,A(0,﹣4),∴AB=OA=CO=BC=4,
过M作MN⊥AB于N,连接MA,由垂径定理得:AN=AB=2,
设⊙M的半径是R,则MN=8﹣R,AM=R,由勾股定理得:AM2=MN2+AN2,
R2=(4﹣R)2+22,解得:R=,∵AN=2,四边形ABCO是正方形,⊙M于x轴相切,
∴M的横坐标是2,即M(2,﹣).故选D.
8A.【解答】解:当AB=AC时,如图:连接AD,∵AB是⊙O的直径,∴AD⊥BC,∴CD=BD,
∵AO=BO,∴OD是△ABC的中位线,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,∴DE是⊙O的切线.
所以B正确.当CD=BD时,AO=BO,∴OD是△ABC的中位线,∴OD∥AC∵DE⊥AC
∴DE⊥OD∴DE是⊙O的切线.所以C正确.当AC∥OD时,∵DE⊥AC,∴DE⊥OD.
∴DE是⊙O的切线.所以D正确.故选A.
9A.【解答】解:∵点M(a,1)在直线BC上,∴OB=1,∵BC∥x轴,∴BC⊥y轴,∴∠OBM=90°,
当BM=OB=1时,△OBM是等腰直角三角形,则∠OMN=45°,此时a=±1;
当BM>OB时,∠OMN<45°,∴a的取值范围是﹣1≤a≤1;故选:A.
10B.【解答】解:连接OD,如图,∵CD为切线,∴OD⊥CD,∵四边形ABCD为平行四边形,
∴∠A=∠C,AB∥CD,∴OD⊥AB,∴∠BOD=90°,∴∠A=∠BOD=45°,∴∠C=45°.
故选B.
二.填空题(共9小题)
11. 2 .
【解答】解:已知圆的直径为13cm,则半径为6.5cm,又圆心距为5.5cm,小于半径,
所以,直线与圆相交,有两个交点.故答案为:2.
12. .
【解答】解:∵()2+()2=2+3=5,()2=5,
∴()2+()2=()2,∴三角形是直角三角形,
∴这个三角形的面积=××=.故答案为:.
13. 115° ; 100° .
【解答】解:∵∠A+∠ABC+∠ACB=180°,∠A=50°,∴∠ABC+∠ACB=130°,
∵I是△ABC的内心,∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=×130°=65°,∴∠BIC=180°﹣(∠IBC+∠ICB)=115°;
当是图1时,由圆周角定理得:∠BOC=2∠A=2×50°=100°;
当是图2时,同样由圆周角定理得:∠BOC=2∠A=100°;
故答案为:115°,100°
14. 10 cm.
【解答】解:∵PA、PB分别与⊙O相切于点A、B,
⊙O的切线EF分别交PA、PB于点E、F,切点C在弧AB上,
∴AE=CE,FB=CF,PA=PB=5,
∴△PEF的周长=PE+EF+PF=PA+PB=10cm,故答案为10
15 4 .
【解答】解:∵AC=6,BC=8,∴AB==10,
∵以点A为圆心,AC长为半径画弧,交AB于点D,∴AD=AC,∴AD=6,
∴BD=AB﹣AD=10﹣6=4.故答案为:4.
16. (4﹣2) m.
【解答】解:连接OB,延长OF,OE分别交BC于H,交AB于K,
∵DE、FG分别与⊙O相切于E、F两点,∴OE⊥ED,OF⊥FG,∵AB∥DE,BC∥FG,
∴OK⊥AB,OH⊥BC,∵∠EOF=90°,∴四边形BKOH是矩形,
∵两组平行墙壁间的走廊宽度都是1m,⊙O半径为1m,∴OK=OH=2,
∴矩形BKOH是正方形,∴∠BOK=∠BOH=45°,∵P是的中点,∴OB经过P点,
在正方形BKOH中,边长=2,∴OB=2,∵OP=1,∴BP=2﹣1,∵p是MN与⊙O的切点,
∴OB⊥MN,∵OB是正方形BKOH的对角线,∴∠OBK=∠OBH=45°,
在△BPM与△BPN中∴△BPM≌△BPN(ASA)∴MP=NP,∴MN=2BP,
∵BP=2﹣1,∴MN=2(2﹣1)=4﹣2,故答案为:4﹣2
17. 125 °.
【解答】解:连接OD,则∠ODC=90°,∠COD=70°;∵OA=OD,∴∠ODA=∠A=∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°,故答案为:125.
18. 12 .
【解答】解:边BC所在的直线与⊙O相切时,
如图,过点G作GN⊥AB,垂足为N,∴EN=NF,又∵EG:EF=:2,∴EG:EN=:1,
又∵GN=AD=8,∴设EN=x,则GE=x,根据勾股定理得:
(x)2﹣x2=64,解得:x=4,GE=4,
设⊙O的半径为r,由OE2=EN2+ON2
得:r2=16+(8﹣r)2,∴r=5.∴OK=NB=5,∴EB=9,又AE=AB,∴AB=12.
故答案为:12.
19. (用含a的代数式表示).
【解答】解:如图,连接PF.设⊙P与直线y=﹣n相切于点E,连接PE.则PE⊥AE.
∵动点P在抛物线y=ax2上,∴设P(m,am2).
∵⊙P恒过点F(0,n),∴PF=PE,即=am2+n.∴n=.
故答案为:.
三.解答题(共6小题)
20.【解答】(1)证明:如图1中,连接OP.
∵AB是小圆的切线,P是切点,∴OP⊥AB,∴PA=PB.
(2)解:如图1中,连接OB.∵大圆的弦AB是小圆的切线,
∴OP⊥AB,AP=PB,∴OB2﹣OP2=(2a÷2)2=a2,
∵S圆环=S大﹣S小=π OB2﹣π OP2=π (OB2﹣OP2),∴S圆环=πa2.
(3)解:如图2中,连接OA,OC,作OE⊥AB于点E.
在Rt△AOE与Rt△OCE中:OE2=OA2﹣AE2,OE2=OC2﹣CE2,
∴OA2﹣AE2=OC2﹣CE2,∴OA2﹣OC2=AE2﹣CE2,∵AB=8,CD=6,∴AE=EB=4,CE=DE=3,
∴OA2﹣OC2=7,∴圆环的面积为:πOA2﹣πOC2=π(OA2﹣OC2)=7π.故答案为7π.
21.【解答】解:如图所示:过点A作AD⊥BC于点D,
由题意可得:AC=700m,∠C=30°,则AD=AC=350m,∵350>300,
∴此公路不会穿过该公园.
22.【解答】解:(1)连接AC,∵点CD是半圆O的三等分点,
∴==,∴∠DAC=∠CAB,∵OA=OC,∴∠CAB=∠OCA,∴∠DAC=∠OCA,
∴AE∥OC(内错角相等,两直线平行)∴∠OCE+∠E=180°,∵CE⊥AD,
∴∠OCE=90°,∴OC⊥CE,∴CE是⊙O的切线;
(2)四边形AOCD为菱形.理由是:∵=,∴∠DCA=∠CAB,∴CD∥OA,
又∵AE∥OC,∴四边形AOCD是平行四边形,∵OA=OC,∴平行四边形AOCD是菱形.
23.【解答】解:(1)∵四边形ABCD是矩形∴∠A=∠B=∠D=90°,BC=AD,AB=CD,
∴∠AFE+∠AEF=90°∵F在AD上,∠EFC=90°∴∠AFE+∠DFC=90°∴∠AEF=∠DFC
∴△AEF∽△DFC∴.∵BE:EA=5:3设BE=5k,AE=3k∴AB=DC=8k,
由勾股定理得:AF=4k,∴∴DF=6k∴BC=AD=10k
在△EBC中,根据勾股定理得BE2+BC2=EC2
∵CE=15 ,BE=5k,BC=10k
∴∴k=3∴AB=8k=24,BC=10k=30
(2)连接OB,由于⊙O内切于以F、E、B、C为顶点的四边形,则BE=EF,BC=CF;
由BE:EA=5:3,设BE=5x,EA=3x,
则FA=4x,CD=8x,又CF=AD,∴CF2=CD2+DF2,即CF2=(8x)2+(CF﹣4x)2,可得CF=10x,DF=6x,则BC=10x;21世纪教育网版权所有
在Rt△EBC中,EB2+BC2=EC2,即(5x)2+(10x)2=15 2,
解得:x=3,则BE=15,BC=30.
再由S△EBC=S△OEB+S△OBC,则 ×BE×BC=×BE×r+×BC×r,解得:r=10;
则⊙O的面积为πr2=100π.
24.【解答】解:(1)连接OC,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=90°,
∵∠CPA=30°,∴∠COP=60°,∵OA=OC,∴∠A=∠ACO=30°,∵PD平分∠APC,
∴∠APD=15°,∴∠CDP=∠A+∠APD=45°.
(2)成立.∵PC是⊙O的切线,∴∠OCP=90°,∵PD是∠CPA的平分线,∴∠APC=2∠APD,
∵OA=OC,∴∠A=∠ACO,∴∠COP=2∠A,
在Rt△OCP中,∠OCP=90°,∴∠COP+∠OPC=90°,∴2(∠A+∠APD)=90°,
∴∠CDP=∠A+∠APD=45°.所以(1)中结论依然成立.
25.【解答】解:(1)∵四边形OABC是矩形,OA=6,AB=4,M是AB的中点,∴OA=6,AM=BM=2,
∴M(6,2);∵直线y=﹣x+3与坐标轴交于D,E,∴当y=0时,﹣x+3=0,
解得:x=3,∴D(3,0);
(2)∵PA=PB,∴点P在线段AB的中垂线上,∴点P的纵坐标是2,
又∵点P在y=﹣x+3上,∴2=﹣x+3,∴x=1,∴点P的坐标为( 1,2);
(3)设P(x,y),连接PN、MN、NF,如图所示:∵点P在y=﹣x+3上,
∴P(x,﹣x+3),
依题意知:PN⊥MN,FN⊥BC,F是圆心,
∴N是线段HB的中点,HN=NB=,PH=4﹣(﹣x+3)=x+1,BM=2,
∵∠HPN+∠HNP=∠HNP+∠BNM=90°,∴∠HPN=∠BNM,又∵∠PHN=∠B=90°,
∴Rt△PNH∽Rt△NMB,∴,∴,
整理得:x2﹣20x+28=0,
解得:x=10+6(不合题意,舍去),或x=10﹣6,
∴梯形PMBH的面积=(BM+PH) BH=(2+10﹣6+1)(6﹣10+6)=51﹣62.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
