第二十五章概率初步数学活动课件
图片预览








文档简介
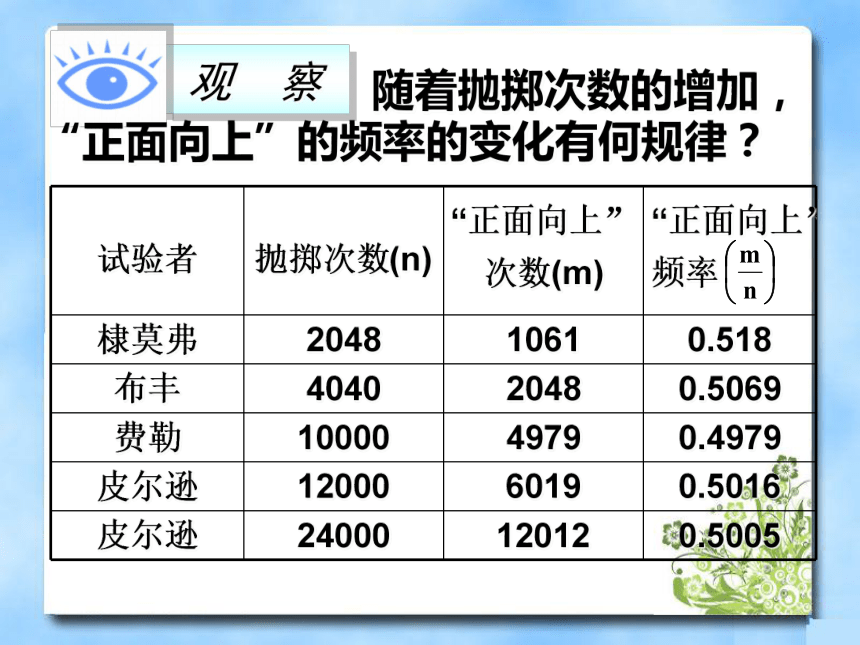
课件21张PPT。数学活动 一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。那这个可能性究竟有多大呢?这就是本节课我们要探讨的问题. 抛掷一枚质地均匀的硬币时, 可能性大的是“正面向上”还是“反面向上” ?试估计这两个事件发生的可能性的大小。 抛掷一枚质地均匀的硬币时,事先无法确定结果是“正面向上”还是“反面向上”,但直觉容易告诉我们这两个随机事件发生的可能性各占一半。如何验证呢? 历史上,有些人曾做过成千上万次抛掷硬币的试验,他们的试验结果是否可以帮我们验证刚得到的猜想呢? 随着抛掷次数的增加,“正面向上”的频率的变化有何规律? 可以发现,在重复抛掷一枚硬币时,“正面向上”的频率在0.5的左右摆动。随着抛掷次数的增加,一般地,频率就呈现出一定的稳定性:在0.5的左右摆动的幅度会越来越小。由于“正面向上”的频率呈现出上述稳定性,我们就用0.5这个常数表示“正面向上”发生的可能性的大小。 由以上的试验中,我们可以知道 “正面向上”的频率。那么,当“正面向上”的频率逐渐稳定到0.5时,“反面向上”的频率有怎样的规律呢? 在抛掷一枚硬币时,结果不是“正面向上”就是“反面向上”, 因此“反面向上”的频率也相应地稳定到0.5。于是我们也用0.5这个常数表示“反面向上”发生的可能性的大小。 由此,试验验证了我们的猜想:抛 掷一枚质地均匀的硬币时,“正面向上”与“反面向上”的可能性相等(各占一半)。 频率表示了事件发生的可能性的大小,那么,频率的范围是怎样的呢? 当A为必然事件时,P(A)是多少?当A为不可能事件时,P(A)是多少? 当A是必然事件时,在n次试验 中,事件A发生的频数 m = n,相应的频率 ,随着n的增加频率始终稳定地为1,因此 P(A)=1.即 P(必然事件)=1. 当A是不可能事件时,在n次试验中,事件A发生的频数m=0,随着n的增加频率始终稳定地为0,因此P(A)=0.即 P(不可能事件)=0. 事件发生的可能性越大,则它的概率越接近1;反之,事件发生的可能性越小,则它的概率越接近0。0≤P(A)≤11、某篮球运动员在同一条件下进行投篮练习,结果如下表所示:0.750.80.80.850.830.80.76 计算表中各对应频率,并根据频率的稳定性估计概率。0.82、抛掷硬币试验结果表:0.50690.50110.50160.50050.51810.49950.53、某批乒乓球产品质量检查结果表:0.90.920.970.940.9540.9510.944、某种油菜籽在相同条件下的发芽试验结果表:0.910.80.8570.8920.9100.8930.9030.90500.9 小明和小刚用如下两 个转盘做游戏,游戏规则 如下:分别旋转两个转盘,当两个转盘所转到的数字之积为奇数时,小明得1分;当所转到的数字之积为偶数时,小刚得1分. 这个游戏对双方公平吗?若公平,说明理由,若不公平,如何修改规则才能使游戏对双方公平?
同课章节目录
