北师大版 八年级数学上册 第三章 3轴对称与坐标变化 教学设计
文档属性
| 名称 | 北师大版 八年级数学上册 第三章 3轴对称与坐标变化 教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 579.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-23 14:21:38 | ||
图片预览



文档简介
第三章 3 轴对称与坐标变化 教学设计
1.在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系.
2.经历图形坐标变化与图形轴对称之间关系的探索过程,发展思维能力和数形结合意识.
经历探究图形的形状、大小、位置关系和变换的过程,掌握空间与图形的基础知识和基本技能,培养学生的探索能力.
1.丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维.
2.通过对图形的研究,激发学生对数学学习的好奇心与求知欲,使学生积极参与数学学习活动.
3.通过“轴对称与坐标变化”,让学生体会数学活动充满着探索性与创造性.
【重点】 经历图形坐标变化与图形轴对称变换之间关系的探索过程,明确图形坐标变化与图形轴对称变换之间的关系.
【难点】 由坐标的变化探索新旧图形之间的变化过程,发展形象思维能力和数形结合意识.
【教师准备】 画图工具,课件.
【学生准备】 画图工具.
导入一:
在前几节课中,我们学习了平面直角坐标系的有关知识.现在我们会画平面直角坐标系;能在方格纸上建立适当的直角坐标系,描述物体的位置;在给定的直角坐标系下,会根据坐标描出点,由点的位置写出它的坐标.
我们知道点的位置不同写出的坐标就不同,反过来,不同的坐标确定不同的点.如果坐标中的横(纵)坐标不变,纵(横)坐标按一定的规律变化,或者横、纵坐标都按一定的规律变化,那么图形是否会变化?变化的规律是怎样的?这是本节课中我们要研究的问题.
导入二:
如图所示的是小刚的脸,如果用(-1,2)表示他的左眼,用(0,0)表示嘴,那么右眼的位置应如何表示?
探索关于两个坐标轴对称的图形的坐标关系
1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么特点?其他对应点的坐标也有这个特点吗?
2.在y轴右边的坐标系内任取一点,做出这个点关于y轴对称的点,看看两个点的坐标有什么样的关系,说说其中的道理.
3.如果关于x轴对称呢?在这个坐标系中作出小旗ABCD关于x轴的对称图形,它的各个顶点的坐标与原来的点的坐标有什么关系?
4.关于x轴对称的两点,它们的横坐标 ,纵坐标 ;?
关于y轴对称的两点,它们的横坐标 ,纵坐标 .?
[设计意图] 通过图形的变化,体会七年级学过的轴对称变换和直角坐标系中的坐标变换的特征.
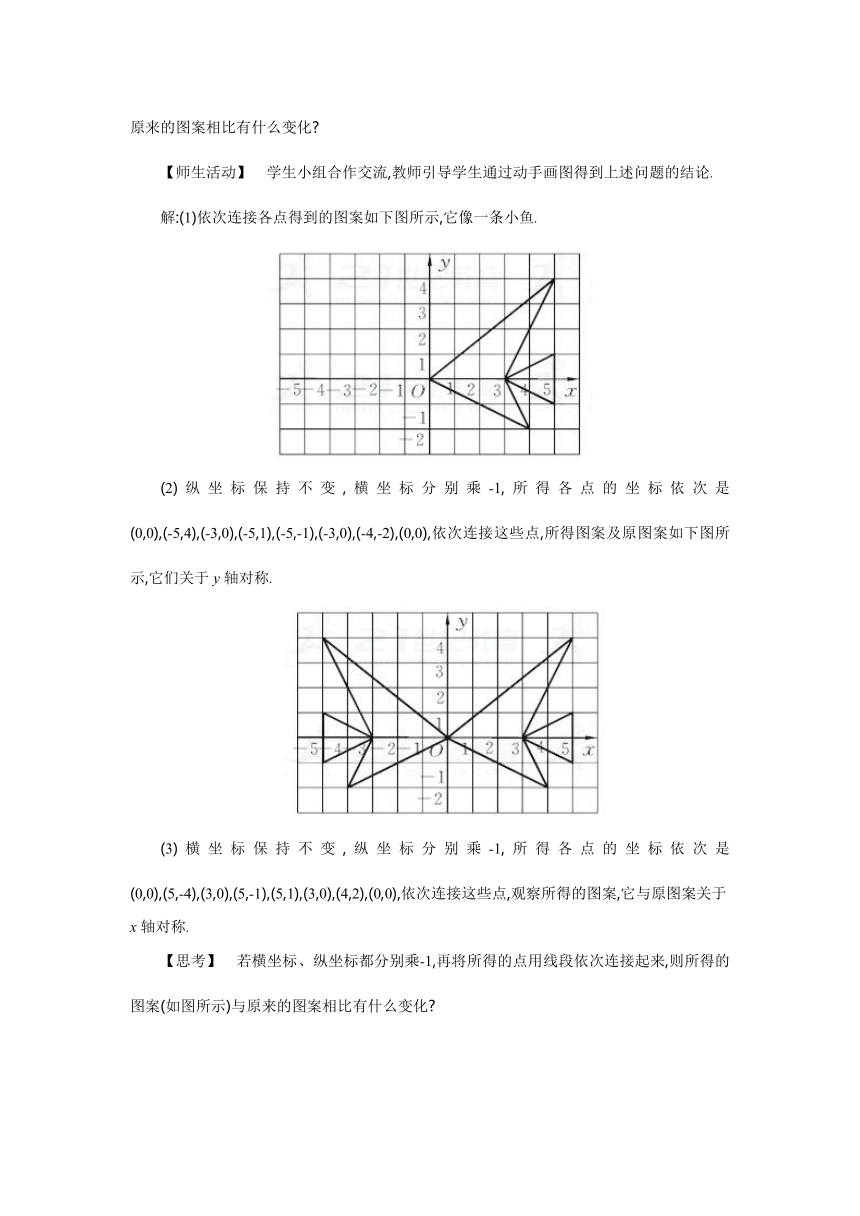
(教材例题)(1)在平面直角坐标系中依次连接下列各点:(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),你得到了一个怎样的图案?
(2)将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接所得各点,你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?
(3)横坐标保持不变,纵坐标分别乘-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
【师生活动】 学生小组合作交流,教师引导学生通过动手画图得到上述问题的结论.
解:(1)依次连接各点得到的图案如下图所示,它像一条小鱼.
(2)纵坐标保持不变,横坐标分别乘-1,所得各点的坐标依次是(0,0),(-5,4),(-3,0),(-5,1),(-5,-1),(-3,0),(-4,-2),(0,0),依次连接这些点,所得图案及原图案如下图所示,它们关于y轴对称.
(3)横坐标保持不变,纵坐标分别乘-1,所得各点的坐标依次是(0,0),(5,-4),(3,0),(5,-1),(5,1),(3,0),(4,2),(0,0),依次连接这些点,观察所得的图案,它与原图案关于x轴对称.
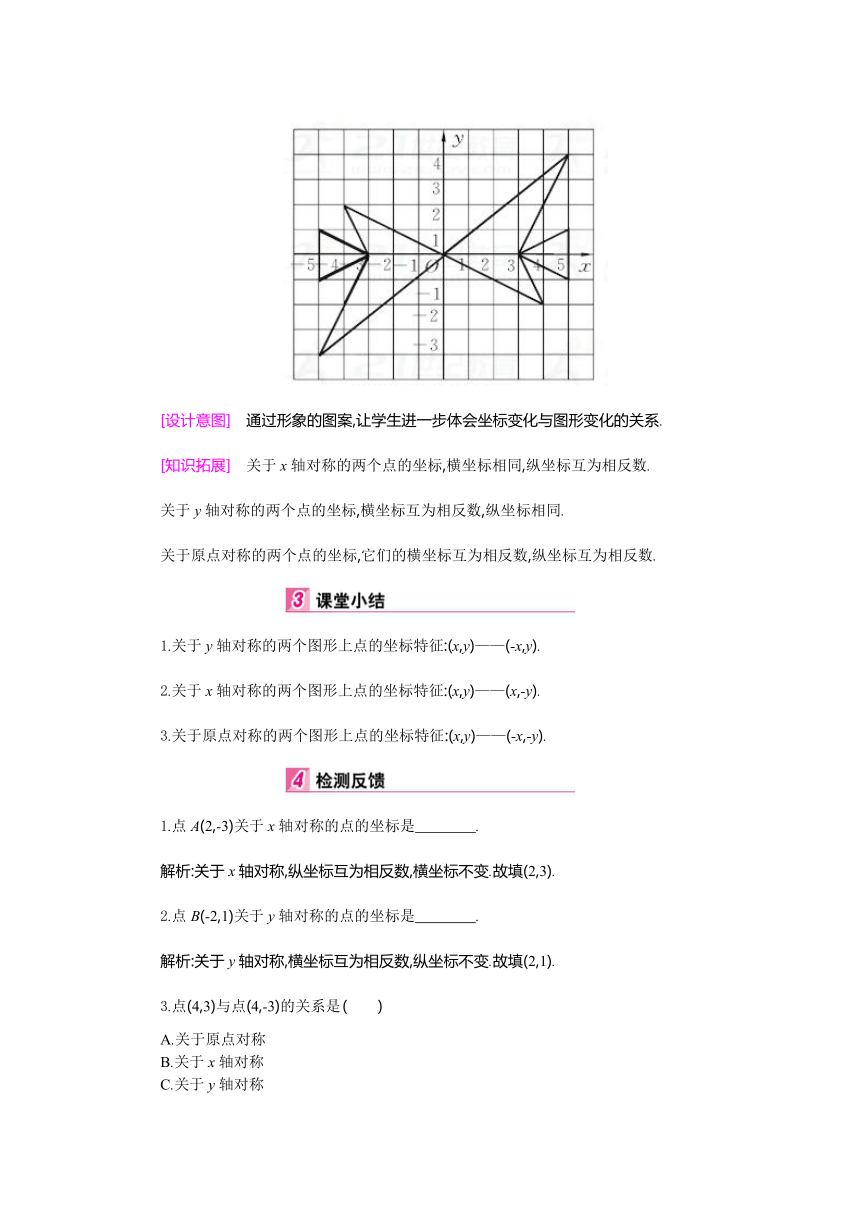
【思考】 若横坐标、纵坐标都分别乘-1,再将所得的点用线段依次连接起来,则所得的图案(如图所示)与原来的图案相比有什么变化?
[设计意图] 通过形象的图案,让学生进一步体会坐标变化与图形变化的关系.
[知识拓展] 关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数.
关于y轴对称的两个点的坐标,横坐标互为相反数,纵坐标相同.
关于原点对称的两个点的坐标,它们的横坐标互为相反数,纵坐标互为相反数.
1.关于y轴对称的两个图形上点的坐标特征:(x,y)——(-x,y).
2.关于x轴对称的两个图形上点的坐标特征:(x,y)——(x,-y).
3.关于原点对称的两个图形上点的坐标特征:(x,y)——(-x,-y).
1.点A(2,-3)关于x轴对称的点的坐标是 .?
解析:关于x轴对称,纵坐标互为相反数,横坐标不变.故填(2,3).
2.点B(-2,1)关于y轴对称的点的坐标是 .?
解析:关于y轴对称,横坐标互为相反数,纵坐标不变.故填(2,1).
3.点(4,3)与点(4,-3)的关系是 ( )
A.关于原点对称
B.关于x轴对称
C.关于y轴对称
D.不构成对称关系
解析:关于x轴对称,纵坐标互为相反数,横坐标不变;关于y轴对称,横坐标互为相反数,纵坐标不变.故选B.
4.点(m,-1)和点(2,n)关于 x轴对称,则 mn等于 ( )
A.-2 B.2 C.1 D.-1
解析:关于x轴对称,纵坐标互为相反数,横坐标不变,则m=2,n=1,mn=2.故选B.
5.(1)若mn=0,则点P(m,n)必定在 上;?
(2)已知点P(a,b),Q(3,6),且PQ∥x轴,则b的值为 .?
解析:(1)mn=0,m=0或n=0,点P(m,n)必定在坐标轴上;(2) PQ∥x轴,P(a,b),Q(3,6)两点纵坐标相同,则b=6.
答案:(1)坐标轴 (2)6
6.点A在第一象限,当m为 时,点A(m+1,3m-5)到 x轴的距离是它到y轴距离的一半.?
解析:点A在第一象限,则横、纵坐标均为正,点A(m+1,3m-5)到 x轴的距离是它到y轴距离的一半,所以m+1=2(3m-5),所以m= .故填.
7.已知A,B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:
①A,B关于x轴对称;②A,B关于y轴对称;③A,B关于原点对称;④A,B之间的距离为4.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
解析:关于x轴对称,纵坐标互为相反数,横坐标不变;关于y轴对称,横坐标互为相反数,纵坐标不变;关于原点对称,横、纵坐标均互为相反数.故选B.
8.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是 ( )
A.4 B.5 C.6 D.7
解析:点A(3,3)关于y轴对称的点为C(-3,3),BC的长就是光线从A点到B点经过的路线长,构造直角三角形,运用勾股定理计算.故选B.
3 轴对称与坐标变化
1.引例.
2.例.
一、教材作业
【必做题】
教材第69页习题3.5第1,2题.
【选做题】
教材第70页习题3.5第4题.
二、课后作业
【基础巩固】
1.如图所示,在直角坐标系中,ΔAOB的顶点O和B的坐标分别是O(0,0),B(6,0),且∠OAB=90°,AO=AB,则顶点A关于x轴的对称点的坐标是 ( )
A.(3,3) B.(-3,3)
C.(3,-3) D.(-3,-3)
2.点M的坐标是(-3,4),则点M关于y轴的对称点的坐标是 ,关于x轴的对称点的坐标是 ,关于原点的对称点的坐标是 ,点M到原点的距离是 .?
【能力提升】
3.ΔABC在平面直角坐标系中的位置如图所示.
(1)作出ΔABC关于x轴对称的ΔA1B1C1,并写出点A1的坐标;
(2)作出ΔABC关于原点对称的ΔA2B2C2,并说出顶点坐标变化的特征.
4.在如图所示的直角坐标系中,四边形ABCD的各顶点的坐标分别是A(0,0),B(2,5),C(9,8),D(12,0),求出这个四边形的面积.
【拓展探究】
5.如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.
如图所示,在直角坐标系中,ΔABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0).点列P1,P2,P3……中的相邻两点都关于ΔABO的一个顶点对称:
点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称……对称中心依次分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2,P7,P100的坐标.
【答案与解析】
1.C
2.(3,4) (-3,-4) (3,-4) 5
3.解:(1)画图略,点A1的坐标是(-2,-3). (2)画图略,关于原点对称的点的横、纵坐标都互为相反数.
4.提示:62.5.
5.解析:通过作图可知6个点一个循环,那么P7的坐标和P1的坐标相同,P100的坐标与P4的坐标一样,通过图中的点可很快求出.
解:作P1关于A点的对称点,即可得到P2(1,-1),由题意知6个点一个循环,故P7的坐标与P1的坐标一样,P100的坐标与P4的坐标一样,所以P7的坐标为(1,1),P100的坐标为(1,-3).
通过本节课的学习,经历坐标变化与图形的轴对称变换之间的关系的探索过程, 掌握空间与图形的基础知识和基本技能,丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维,激发学生对数学学习的好奇心与求知欲.学生能积极参与数学学习活动,积极交流合作,体验数学活动充满着探索与创造性.
以前学过的轴对称知识个别学生可能有些遗忘,致使理解不好,掌握不够扎实.
事先一定要准备好坐标纸等,提高学习效率. 在开始设计复习轴对称的知识和题目,在复习中引入新课,新旧结合,减少遗忘带来的麻烦.
习题3.5(教材第69页)
1.解:ΔDEF与ΔABC关于y轴对称,它们相应顶点的横坐标互为相反数,纵坐标相等;ΔPMN与ΔABC关于x轴对称,它们相应顶点的横坐标相等,纵坐标互为相反数.
2.解:找出点A,B,C关于x轴对称的点A1,B1,C1,连接A1B1,B1C1,C1A1,得到ΔA1B1C1,ΔA1B1C1与ΔABC关于x轴对称;找出点A1,B1,C1关于y轴对称的点A2,B2,C2,连接A2B2,B2C2,C2A2,得到ΔA2B2C2,ΔA2B2C2与ΔA1B1C1关于y轴对称.画图略.
3.提示:各个顶点的坐标分别为I(-6,0),A(6,0),M(0,-6),E(0,6),G(-3,3),C(3,3),O(3,-3),K(-3,-3),H(-2,1),B(2,1),P(2,-1),J(-2,-1),F(-1,2),D(1,2),N(1,-2),L(-1,-2).特点略.
4.提示:利用关于坐标轴对称的点的规律作图.
复习题(教材第71页)
1.解:(1)A(-4,0). (2)B(0,4). (3)C(-4,4).
2.解:点(0,a)在纵轴的正半轴上;点(b,0)在横轴的正半轴上.
3.提示:答案不唯一,可以以长方形左下角的顶点为坐标原点,过这个顶点的两边所在的直线为坐标轴,建立平面直角坐标系.此时四个顶点的坐标分别为(0,0),(8,0),(8,6),(0,6).
4.解:画图略.(1)这个图案与原图案关于y轴对称.
(2)这个图案与原图案关于x轴对称.
6.解:画图略.(1)所得图案与原图案关于y轴对称.
(2)所得图案与原图案关于x轴对称.
7.解:可能,如本身关于y轴对称的图形.
8.解:如图所示.交流略.
9.解:(1)与x轴平行的直线上的点的纵坐标相等,与y轴平行的直线上的点的横坐标相等. (2)若a,b同号,则点P(a,b)在第一或第三象限;若a,b异号,则点P(a,b)在第二或第四象限.
13.提示:可以根据轴对称的意义来完成,也可以根据轴对称的点的坐标特征来完成.
14.解:分别过B,C作x轴的垂线,垂足分别为E,F,则E,F的坐标分别为(3,0),(14,0),则S四边形ABCD=SΔABE+S梯形BEFC+SΔCFD.因为SΔABE=AE·BE=×3×6=9,S梯形BEFC=(BE+CF)·EF=(6+8)×11=77,SΔCFD=FD·CF=×2×8=8,所以S四边形ABCD=9+77+8=94.
1.教学解读.
学生的知识技能基础:学生已学习了运用多种方法确定物体的位置,使学生感受到了丰富的确定位置的现实背景;系统学习了平面直角坐标系的基本概念,能在平面直角坐标系中准确地表示物体的位置,清楚地认识了点和坐标之间的对应关系;能确定点的坐标及根据坐标描点,进而连线形成图形.
学生的活动经验基础:学生有了一定的合作学习的基础及学习能力,教学中要安排一定的合作交流与自主学习的机会,加强学生之间的交流.
2.重难点突破.
对称点的坐标变化规律:对称点的坐标情况可以简记为:关于横轴对称,则“横不变,纵相反”;关于纵轴对称,则“纵不变,横相反”;关于原点对称,则“全相反”.
如图所示,在平面直角坐标系中,求三角形ABO的面积.
解:过A,B分别向x轴、y轴作垂线AE,BN,NB与EA的延长线相交于M点.
SΔOAB=S正方形OEMN-SΔOAE-SΔOBN-SΔABM=9-×3×2-×3×1 -×2×1=9-3-1.5-1=3.5.
如图所示,在ΔAOB中,A,B两点的坐标分别为(2,4)和(6,2),求ΔAOB的面积.
解:SΔAOB=S四边形ABNO-SΔBON=×2×4+×(2+4)×4-×6×2=4+12-6=10.
于任何象限.故选D.
【针对训练1】 点P(m,1)在第二象限内,则点Q(-m,0)在 ( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
〔解析〕 第二象限点的坐标符号为(-,+),点P(m,1)在第二象限内,所以m<0,则-m>0,点Q(-m,0)的纵坐标为0,所以点Q(-m,0)在x轴正半轴上.故选A.
[方法归纳] 在平面直角坐标系中,四个象限的点的坐标符号为:第一象限(+,+), 第二象限(-,+),第三象限(-,-),第四象限(+,-).在x轴上,纵坐标为0,在y轴上,横坐标为0,原点坐标为(0,0).
专题二 用坐标表示位置
【专题分析】
用坐标表示位置,需要我们根据特殊点的坐标建立适当的坐标系,然后找到所需要的地点的坐标.
如图所示,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点 ( )
A.(-1,1) B.(-2,-1)
C.(-3,1) D.(1,-2)
〔解析〕 由“帅”位于点(-1,-2),“马”位于点(2,-2),可得直角坐标系的原点,则可建立平面直角坐标系,得到“兵”位于点(-3,1).故选C.
[方法归纳] 根据已知点的坐标寻找坐标原点是解这类题目的关键,找到原点,建立直角坐标系,再找到需要的点的坐标.
【针对训练2】 如图所示的是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(3,1),(3,5)表示图书馆和教学楼的位置,那么实验楼的位置应表示为 .?
〔解析〕 由(3,1),(3,5)表示的位置确定直角坐标系,再找到实验楼的位置.故填(-3,4).
专题三 数形结合思想
【专题分析】
本章涉及的数学思想主要是数形结合思想,简单地说,数形结合,就是通过代数来解决几何问题,代数问题能通过几何图形来表示和解决,平面直角坐标系就是这两者的有机结合,在平面直角坐标系中,我们画出图形,通过代数的方法,来解决各种问题,包括以后学到的函数等,本章中涉及得比较简单,主要有在平面直角坐标系中表示点的坐标,用点的坐标表示图形的变换,求某些特殊图形的面积等.
如图所示,若将直角坐标系中“鱼”的每个“顶点”的纵坐标分别变为原来的,横坐标不变,则点A的对应点的坐标是 ( )
A.(-4,3) B.(4,3)
C.(-2,6) D.(-2,3)
〔解析〕 在题图中,点A的坐标是(-4,6),横坐标不变,纵坐标变为原来的后,纵坐标变为3.故选A.
【针对训练3】 如图所示,三角形ABC在直角坐标系中.
(1)请写出三角形ABC各顶点的坐标;
(2)求三角形ABC的面积.
〔解析〕 明确坐标系的原点,分别找出各顶点的坐标即可,求三角形ABC的面积,可把求三角形的面积转化为求一个长方形面积与三个直角三角形面积差的问题.
解:(1)A(-1,-1),B(4,2),C(1,3).
(2)SΔABC=5×4-×5×3-×1×3-×2×4=7.
[方法归纳] 掌握平面直角坐标系的特征是解决这类问题的关键,用代数的计算方法和表示方法表示点的坐标,表示线段的长,表示图形的面积和某些规律性的结论.
【针对训练4】 如图所示,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第二次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2013次运动后,动点P的坐标是 ,经过第2014次运动后,动点P的坐标是 .?
〔解析〕 寻找规律:横坐标就是运动的次数,次数为偶数时纵坐标为0,次数为奇数时纵坐标为1,2循环.
〔答案〕 (2013,1) (2014,0)
1.在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系.
2.经历图形坐标变化与图形轴对称之间关系的探索过程,发展思维能力和数形结合意识.
经历探究图形的形状、大小、位置关系和变换的过程,掌握空间与图形的基础知识和基本技能,培养学生的探索能力.
1.丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维.
2.通过对图形的研究,激发学生对数学学习的好奇心与求知欲,使学生积极参与数学学习活动.
3.通过“轴对称与坐标变化”,让学生体会数学活动充满着探索性与创造性.
【重点】 经历图形坐标变化与图形轴对称变换之间关系的探索过程,明确图形坐标变化与图形轴对称变换之间的关系.
【难点】 由坐标的变化探索新旧图形之间的变化过程,发展形象思维能力和数形结合意识.
【教师准备】 画图工具,课件.
【学生准备】 画图工具.
导入一:
在前几节课中,我们学习了平面直角坐标系的有关知识.现在我们会画平面直角坐标系;能在方格纸上建立适当的直角坐标系,描述物体的位置;在给定的直角坐标系下,会根据坐标描出点,由点的位置写出它的坐标.
我们知道点的位置不同写出的坐标就不同,反过来,不同的坐标确定不同的点.如果坐标中的横(纵)坐标不变,纵(横)坐标按一定的规律变化,或者横、纵坐标都按一定的规律变化,那么图形是否会变化?变化的规律是怎样的?这是本节课中我们要研究的问题.
导入二:
如图所示的是小刚的脸,如果用(-1,2)表示他的左眼,用(0,0)表示嘴,那么右眼的位置应如何表示?
探索关于两个坐标轴对称的图形的坐标关系
1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么特点?其他对应点的坐标也有这个特点吗?
2.在y轴右边的坐标系内任取一点,做出这个点关于y轴对称的点,看看两个点的坐标有什么样的关系,说说其中的道理.
3.如果关于x轴对称呢?在这个坐标系中作出小旗ABCD关于x轴的对称图形,它的各个顶点的坐标与原来的点的坐标有什么关系?
4.关于x轴对称的两点,它们的横坐标 ,纵坐标 ;?
关于y轴对称的两点,它们的横坐标 ,纵坐标 .?
[设计意图] 通过图形的变化,体会七年级学过的轴对称变换和直角坐标系中的坐标变换的特征.
(教材例题)(1)在平面直角坐标系中依次连接下列各点:(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0),你得到了一个怎样的图案?
(2)将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接所得各点,你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?
(3)横坐标保持不变,纵坐标分别乘-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
【师生活动】 学生小组合作交流,教师引导学生通过动手画图得到上述问题的结论.
解:(1)依次连接各点得到的图案如下图所示,它像一条小鱼.
(2)纵坐标保持不变,横坐标分别乘-1,所得各点的坐标依次是(0,0),(-5,4),(-3,0),(-5,1),(-5,-1),(-3,0),(-4,-2),(0,0),依次连接这些点,所得图案及原图案如下图所示,它们关于y轴对称.
(3)横坐标保持不变,纵坐标分别乘-1,所得各点的坐标依次是(0,0),(5,-4),(3,0),(5,-1),(5,1),(3,0),(4,2),(0,0),依次连接这些点,观察所得的图案,它与原图案关于x轴对称.
【思考】 若横坐标、纵坐标都分别乘-1,再将所得的点用线段依次连接起来,则所得的图案(如图所示)与原来的图案相比有什么变化?
[设计意图] 通过形象的图案,让学生进一步体会坐标变化与图形变化的关系.
[知识拓展] 关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数.
关于y轴对称的两个点的坐标,横坐标互为相反数,纵坐标相同.
关于原点对称的两个点的坐标,它们的横坐标互为相反数,纵坐标互为相反数.
1.关于y轴对称的两个图形上点的坐标特征:(x,y)——(-x,y).
2.关于x轴对称的两个图形上点的坐标特征:(x,y)——(x,-y).
3.关于原点对称的两个图形上点的坐标特征:(x,y)——(-x,-y).
1.点A(2,-3)关于x轴对称的点的坐标是 .?
解析:关于x轴对称,纵坐标互为相反数,横坐标不变.故填(2,3).
2.点B(-2,1)关于y轴对称的点的坐标是 .?
解析:关于y轴对称,横坐标互为相反数,纵坐标不变.故填(2,1).
3.点(4,3)与点(4,-3)的关系是 ( )
A.关于原点对称
B.关于x轴对称
C.关于y轴对称
D.不构成对称关系
解析:关于x轴对称,纵坐标互为相反数,横坐标不变;关于y轴对称,横坐标互为相反数,纵坐标不变.故选B.
4.点(m,-1)和点(2,n)关于 x轴对称,则 mn等于 ( )
A.-2 B.2 C.1 D.-1
解析:关于x轴对称,纵坐标互为相反数,横坐标不变,则m=2,n=1,mn=2.故选B.
5.(1)若mn=0,则点P(m,n)必定在 上;?
(2)已知点P(a,b),Q(3,6),且PQ∥x轴,则b的值为 .?
解析:(1)mn=0,m=0或n=0,点P(m,n)必定在坐标轴上;(2) PQ∥x轴,P(a,b),Q(3,6)两点纵坐标相同,则b=6.
答案:(1)坐标轴 (2)6
6.点A在第一象限,当m为 时,点A(m+1,3m-5)到 x轴的距离是它到y轴距离的一半.?
解析:点A在第一象限,则横、纵坐标均为正,点A(m+1,3m-5)到 x轴的距离是它到y轴距离的一半,所以m+1=2(3m-5),所以m= .故填.
7.已知A,B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:
①A,B关于x轴对称;②A,B关于y轴对称;③A,B关于原点对称;④A,B之间的距离为4.
其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
解析:关于x轴对称,纵坐标互为相反数,横坐标不变;关于y轴对称,横坐标互为相反数,纵坐标不变;关于原点对称,横、纵坐标均互为相反数.故选B.
8.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是 ( )
A.4 B.5 C.6 D.7
解析:点A(3,3)关于y轴对称的点为C(-3,3),BC的长就是光线从A点到B点经过的路线长,构造直角三角形,运用勾股定理计算.故选B.
3 轴对称与坐标变化
1.引例.
2.例.
一、教材作业
【必做题】
教材第69页习题3.5第1,2题.
【选做题】
教材第70页习题3.5第4题.
二、课后作业
【基础巩固】
1.如图所示,在直角坐标系中,ΔAOB的顶点O和B的坐标分别是O(0,0),B(6,0),且∠OAB=90°,AO=AB,则顶点A关于x轴的对称点的坐标是 ( )
A.(3,3) B.(-3,3)
C.(3,-3) D.(-3,-3)
2.点M的坐标是(-3,4),则点M关于y轴的对称点的坐标是 ,关于x轴的对称点的坐标是 ,关于原点的对称点的坐标是 ,点M到原点的距离是 .?
【能力提升】
3.ΔABC在平面直角坐标系中的位置如图所示.
(1)作出ΔABC关于x轴对称的ΔA1B1C1,并写出点A1的坐标;
(2)作出ΔABC关于原点对称的ΔA2B2C2,并说出顶点坐标变化的特征.
4.在如图所示的直角坐标系中,四边形ABCD的各顶点的坐标分别是A(0,0),B(2,5),C(9,8),D(12,0),求出这个四边形的面积.
【拓展探究】
5.如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.
如图所示,在直角坐标系中,ΔABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0).点列P1,P2,P3……中的相邻两点都关于ΔABO的一个顶点对称:
点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称……对称中心依次分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2,P7,P100的坐标.
【答案与解析】
1.C
2.(3,4) (-3,-4) (3,-4) 5
3.解:(1)画图略,点A1的坐标是(-2,-3). (2)画图略,关于原点对称的点的横、纵坐标都互为相反数.
4.提示:62.5.
5.解析:通过作图可知6个点一个循环,那么P7的坐标和P1的坐标相同,P100的坐标与P4的坐标一样,通过图中的点可很快求出.
解:作P1关于A点的对称点,即可得到P2(1,-1),由题意知6个点一个循环,故P7的坐标与P1的坐标一样,P100的坐标与P4的坐标一样,所以P7的坐标为(1,1),P100的坐标为(1,-3).
通过本节课的学习,经历坐标变化与图形的轴对称变换之间的关系的探索过程, 掌握空间与图形的基础知识和基本技能,丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维,激发学生对数学学习的好奇心与求知欲.学生能积极参与数学学习活动,积极交流合作,体验数学活动充满着探索与创造性.
以前学过的轴对称知识个别学生可能有些遗忘,致使理解不好,掌握不够扎实.
事先一定要准备好坐标纸等,提高学习效率. 在开始设计复习轴对称的知识和题目,在复习中引入新课,新旧结合,减少遗忘带来的麻烦.
习题3.5(教材第69页)
1.解:ΔDEF与ΔABC关于y轴对称,它们相应顶点的横坐标互为相反数,纵坐标相等;ΔPMN与ΔABC关于x轴对称,它们相应顶点的横坐标相等,纵坐标互为相反数.
2.解:找出点A,B,C关于x轴对称的点A1,B1,C1,连接A1B1,B1C1,C1A1,得到ΔA1B1C1,ΔA1B1C1与ΔABC关于x轴对称;找出点A1,B1,C1关于y轴对称的点A2,B2,C2,连接A2B2,B2C2,C2A2,得到ΔA2B2C2,ΔA2B2C2与ΔA1B1C1关于y轴对称.画图略.
3.提示:各个顶点的坐标分别为I(-6,0),A(6,0),M(0,-6),E(0,6),G(-3,3),C(3,3),O(3,-3),K(-3,-3),H(-2,1),B(2,1),P(2,-1),J(-2,-1),F(-1,2),D(1,2),N(1,-2),L(-1,-2).特点略.
4.提示:利用关于坐标轴对称的点的规律作图.
复习题(教材第71页)
1.解:(1)A(-4,0). (2)B(0,4). (3)C(-4,4).
2.解:点(0,a)在纵轴的正半轴上;点(b,0)在横轴的正半轴上.
3.提示:答案不唯一,可以以长方形左下角的顶点为坐标原点,过这个顶点的两边所在的直线为坐标轴,建立平面直角坐标系.此时四个顶点的坐标分别为(0,0),(8,0),(8,6),(0,6).
4.解:画图略.(1)这个图案与原图案关于y轴对称.
(2)这个图案与原图案关于x轴对称.
6.解:画图略.(1)所得图案与原图案关于y轴对称.
(2)所得图案与原图案关于x轴对称.
7.解:可能,如本身关于y轴对称的图形.
8.解:如图所示.交流略.
9.解:(1)与x轴平行的直线上的点的纵坐标相等,与y轴平行的直线上的点的横坐标相等. (2)若a,b同号,则点P(a,b)在第一或第三象限;若a,b异号,则点P(a,b)在第二或第四象限.
13.提示:可以根据轴对称的意义来完成,也可以根据轴对称的点的坐标特征来完成.
14.解:分别过B,C作x轴的垂线,垂足分别为E,F,则E,F的坐标分别为(3,0),(14,0),则S四边形ABCD=SΔABE+S梯形BEFC+SΔCFD.因为SΔABE=AE·BE=×3×6=9,S梯形BEFC=(BE+CF)·EF=(6+8)×11=77,SΔCFD=FD·CF=×2×8=8,所以S四边形ABCD=9+77+8=94.
1.教学解读.
学生的知识技能基础:学生已学习了运用多种方法确定物体的位置,使学生感受到了丰富的确定位置的现实背景;系统学习了平面直角坐标系的基本概念,能在平面直角坐标系中准确地表示物体的位置,清楚地认识了点和坐标之间的对应关系;能确定点的坐标及根据坐标描点,进而连线形成图形.
学生的活动经验基础:学生有了一定的合作学习的基础及学习能力,教学中要安排一定的合作交流与自主学习的机会,加强学生之间的交流.
2.重难点突破.
对称点的坐标变化规律:对称点的坐标情况可以简记为:关于横轴对称,则“横不变,纵相反”;关于纵轴对称,则“纵不变,横相反”;关于原点对称,则“全相反”.
如图所示,在平面直角坐标系中,求三角形ABO的面积.
解:过A,B分别向x轴、y轴作垂线AE,BN,NB与EA的延长线相交于M点.
SΔOAB=S正方形OEMN-SΔOAE-SΔOBN-SΔABM=9-×3×2-×3×1 -×2×1=9-3-1.5-1=3.5.
如图所示,在ΔAOB中,A,B两点的坐标分别为(2,4)和(6,2),求ΔAOB的面积.
解:SΔAOB=S四边形ABNO-SΔBON=×2×4+×(2+4)×4-×6×2=4+12-6=10.
于任何象限.故选D.
【针对训练1】 点P(m,1)在第二象限内,则点Q(-m,0)在 ( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
〔解析〕 第二象限点的坐标符号为(-,+),点P(m,1)在第二象限内,所以m<0,则-m>0,点Q(-m,0)的纵坐标为0,所以点Q(-m,0)在x轴正半轴上.故选A.
[方法归纳] 在平面直角坐标系中,四个象限的点的坐标符号为:第一象限(+,+), 第二象限(-,+),第三象限(-,-),第四象限(+,-).在x轴上,纵坐标为0,在y轴上,横坐标为0,原点坐标为(0,0).
专题二 用坐标表示位置
【专题分析】
用坐标表示位置,需要我们根据特殊点的坐标建立适当的坐标系,然后找到所需要的地点的坐标.
如图所示,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点 ( )
A.(-1,1) B.(-2,-1)
C.(-3,1) D.(1,-2)
〔解析〕 由“帅”位于点(-1,-2),“马”位于点(2,-2),可得直角坐标系的原点,则可建立平面直角坐标系,得到“兵”位于点(-3,1).故选C.
[方法归纳] 根据已知点的坐标寻找坐标原点是解这类题目的关键,找到原点,建立直角坐标系,再找到需要的点的坐标.
【针对训练2】 如图所示的是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),如果分别用(3,1),(3,5)表示图书馆和教学楼的位置,那么实验楼的位置应表示为 .?
〔解析〕 由(3,1),(3,5)表示的位置确定直角坐标系,再找到实验楼的位置.故填(-3,4).
专题三 数形结合思想
【专题分析】
本章涉及的数学思想主要是数形结合思想,简单地说,数形结合,就是通过代数来解决几何问题,代数问题能通过几何图形来表示和解决,平面直角坐标系就是这两者的有机结合,在平面直角坐标系中,我们画出图形,通过代数的方法,来解决各种问题,包括以后学到的函数等,本章中涉及得比较简单,主要有在平面直角坐标系中表示点的坐标,用点的坐标表示图形的变换,求某些特殊图形的面积等.
如图所示,若将直角坐标系中“鱼”的每个“顶点”的纵坐标分别变为原来的,横坐标不变,则点A的对应点的坐标是 ( )
A.(-4,3) B.(4,3)
C.(-2,6) D.(-2,3)
〔解析〕 在题图中,点A的坐标是(-4,6),横坐标不变,纵坐标变为原来的后,纵坐标变为3.故选A.
【针对训练3】 如图所示,三角形ABC在直角坐标系中.
(1)请写出三角形ABC各顶点的坐标;
(2)求三角形ABC的面积.
〔解析〕 明确坐标系的原点,分别找出各顶点的坐标即可,求三角形ABC的面积,可把求三角形的面积转化为求一个长方形面积与三个直角三角形面积差的问题.
解:(1)A(-1,-1),B(4,2),C(1,3).
(2)SΔABC=5×4-×5×3-×1×3-×2×4=7.
[方法归纳] 掌握平面直角坐标系的特征是解决这类问题的关键,用代数的计算方法和表示方法表示点的坐标,表示线段的长,表示图形的面积和某些规律性的结论.
【针对训练4】 如图所示,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第二次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2013次运动后,动点P的坐标是 ,经过第2014次运动后,动点P的坐标是 .?
〔解析〕 寻找规律:横坐标就是运动的次数,次数为偶数时纵坐标为0,次数为奇数时纵坐标为1,2循环.
〔答案〕 (2013,1) (2014,0)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
