北师大版 八年级数学上册 第四章 2一次函数与正比例函数 教学设计
文档属性
| 名称 | 北师大版 八年级数学上册 第四章 2一次函数与正比例函数 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-23 00:00:00 | ||
图片预览




文档简介
第四章 2 一次函数与正比例函数 教学设计
理解一次函数和正比例函数的概念,以及两者之间的关系,利用一次函数和正比例函数解决实际问题.
能够根据所给条件写出简单的一次函数表达式,并利用它解决实际问题.
1.通过函数与变量之间的联系,一次函数与一次方程的联系,提高学生的数学思维能力.
2.经历利用一次函数解决实际问题的过程,发展学生的数学应用能力.
【重点】
1.一次函数、正比例函数的概念.
2.一次函数、正比例函数的关系.
3.会根据已知信息写出一次函数的表达式.
【难点】 一次函数知识的运用.
【教师准备】 引例和例题投影图片.
【学生准备】 复习函数的定义、函数值等内容.
导入一:
生活中充满着许许多多变化的量,你了解这些变量之间的关系吗?如弹簧的长度(在弹性限度内)与所挂物体的质量,输液时间与相应时间内水滴数目……了解这些关系,可以帮助我们更好地认识世界.函数是刻画变量之间关系的常用模型,其中最为简单的是一次函数,那么什么是一次函数?用一次函数可以解决哪些问题呢?你想了解这些吗?一起进入这节课的学习吧!
导入二:
汽车的平均速度为95 km/h,A地直达北京的高速公路全程为570 km,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己与北京的距离.小明能得到一个什么样的关系式呢?他是怎样想的?猜猜看.
[过渡语] 怎样写出两个变量之间的函数关系式呢?
一、出示教材引例及问题
某弹簧的自然长度为3 cm.在弹性限度内,所挂物体的质量x每增加1 kg,弹簧长度y增加0.5 cm.
(1)计算所挂物体的质量分别为1 kg,2 kg,3 kg,4 kg,5 kg时弹簧的长度,并填入下表:
x/kg
0
1
2
3
4
5
y/cm
(2)你能写出y与x之间的关系式吗?
【分析】 当不挂物体时,弹簧长度为3厘米,当挂1千克物体时,增加0.5厘米,总长度为3.5厘米,增加1千克物体,即所挂物体为2千克时,弹簧又增加0.5厘米,总共增加1厘米,由此可见,所挂物体为x千克时,弹簧就伸长0.5x厘米,则弹簧总长为原长加伸长的长度,即y=3+0.5x.
二、做一做
某辆汽车油箱中原有汽油60 L,汽车每行驶50 km耗油6 L.
(1)完成下表:
汽车行驶
路程x/km
0
50
100
150
200
300
耗油量y/L
(2)你能写出耗油量y(L)与汽车行驶路程x(km)之间的关系式吗?
(3)你能写出油箱剩余油量z(L)与汽车行驶路程x(km)之间的关系式吗?
【答案与提示】 (1)如下表所示:
汽车行驶
路程x/km
0
50
100
150
200
300
耗油量y/L
0
6
12
18
24
36
(2)y=6·x.
(3)z=60-x.
【归纳】 若两个变量x,y间的对应关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.例如y=2x+1, y=x-1等都是一次函数.
特别地,当b=0时,称y是x的正比例函数.例如,y=2x,y=-3x等都是正比例函数.
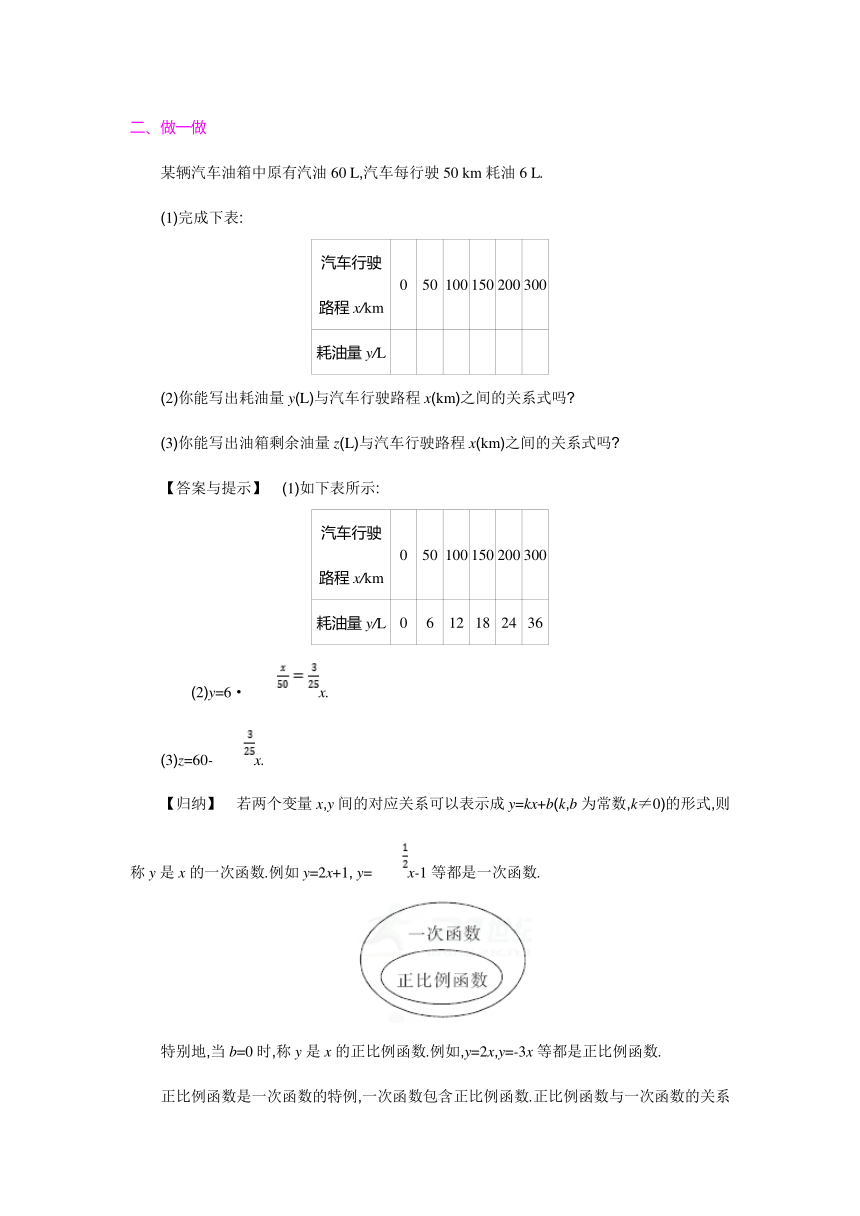
正比例函数是一次函数的特例,一次函数包含正比例函数.正比例函数与一次函数的关系如图所示.
[知识拓展] 正比例函数也是一次函数,不过是特殊的一次函数,就像是等边三角形与等腰三角形的关系一样.
三、例题讲解
写出下列各题中y与x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60 km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系;
(2)圆的面积y(cm2)与它的半径x(cm)之间的关系;
(3)某水池有水15 m3,现打开进水管进水,进水速度为5 m3/h,x h后这个水池内有水y m3.
(由学生交流讨论完成)
解:(1)由路程=速度×时间,得y=60x,y是x的一次函数,也是x的正比例函数.
(2)由圆的面积公式,得y=πx2,y不是x的正比例函数,也不是x的一次函数.
(3)这个水池每小时增加5 m3水,x h增加5x m3水,因而y=15+5x,y是x的一次函数,但不是x的正比例函数.
【思考】 两个变量之间存在函数关系,它们之间一定是一次函数或正比例函数关系吗?
我国自2011年9月1日起,个人工资、薪金所得税征收办法规定:月收入不超过3500元的部分不收税;月收入超过3500元但不超过5000元的部分征收3%的所得税……如某人月收入3860元,他应缴纳个人工资、薪金所得税为(3860-3500)×3%=10.8(元).
(1)当月收入超过3500元而又不超过5000元时,写出应缴纳个人工资、薪金所得税y(元)与月收入x(元)之间的关系式;
(2)某人月收入为4160元,他应缴纳个人工资、薪金所得税多少元?
(3)如果某人本月缴纳个人工资、薪金所得税19.2元,那么此人本月工资、薪金收入是多少元?
〔解析〕 一次函数y=kx+b(k,b为常数,k≠0)中,自变量的取值范围是全体实数,但是在实际问题中,要根据具体情况来确定该一次函数的自变量的取值范围.本例题的关键是确定问题当中的x的取值范围.
解:(1)当月收入超过3500元而不超过5000元时,
y=(x-3500)×3%,即y=0.03x-105.
(2)当x=4160时,y=0.03×4160-105=19.8(元)
(3)因为(5000-3500)×3%=45(元),19.2<45,所以此人本月工资、薪金收入不超过5000元.设此人本月工资、薪金收入是x元,则:
19.2=0.03x-105,x=4140.
即此人本月工资、薪金收入是4140元.
1.一根弹簧的原长为12 cm,它能挂的重量不能超过15 kg并且每挂重物1 kg就伸长0.5 cm,则在弹性限度内,挂重物后的弹簧长度y(cm)与所挂重物x(kg)之间的函数关系式是 .?
解析:弹簧伸长后的长度等于原长加上挂重物后伸长的长度,所以y=0.5x+12.由于这是实际问题,自变量的取值要有实际意义,所以0≤x≤15.故填y=0.5x+12(0≤x≤15).
2.y=kx+b是一次函数,则k为 ( )
A.一切实数 B.正实数
C.负实数 D.非零实数
解析:y=kx+b是一次函数,也就是说kx+b是关于x的一次式,所以k是不等于0的实数.故选D.
3.下列函数中,y是x的一次函数的是 ( )
A.y=-3x+5 B.y=-3x2
C.y= D.y=2
解析:形如y=kx+b(k,b为常数,k≠0)的函数是一次函数.故选A.
4.下列说法不正确的是 ( )
A.一次函数不一定是正比例函数
B.不是一次函数就一定不是正比例函数
C.正比例函数是特殊的一次函数
D.不是正比例函数就一定不是一次函数
解析:正比例函数是特殊的一次函数,不是正比例函数也可能是一次函数,如y=2x-3.故选D.
5.某面包厂现年产值是15万元,计划从今年开始每年增加产值2万元.
(1)写出年产值y(万元)与年数x之间的函数表达式;
(2)求5年后的年产值.
解析:(1)年产值等于现年产值加上每年增加的年产值乘年数.(2)将x=5代入(1)中求得的表达式即可得解.
解:(1)y=2x+15.
(2)当x=5时,y=2×5+15=25,
即5年后的年产值为25万元.
2 一次函数与正比例函数
1.出示教材引例及问题.
2.做一做.
3.例题讲解.
例1
例2
一、教材作业
【必做题】
教材第82页习题4.2第1,2题.
【选做题】
教材第82页习题4.2第5题.
二、课后作业
【基础巩固】
1.若函数y=(m-5)x+(4m+1)x2(m为常数)中的y与x成正比例,则m的取值范围为 ( )
A.m>- B.m> 5
C.m=- D.m=5
2.下列函数:①y=4x+3;②y=x;③y=x4;④y=x2;⑤y=1-x中,一次函数有 ( )
A.1个 B.2个 C.3个 D.4个
3.在函数y=x, y=x+3,y=,y=2x2-3, y=2(x-3)中, 是关于x的正比例函数.?
【能力提升】
4.容积为800 L的水池内已蓄水200 L,若每分钟注入的水量是15 L,设池内的水量为Q(L),注水时间为t(min).
(1)请写出Q与t的函数关系式;
(2)注水多长时间可以把水池注满?
(3)当注水时间为0. 2 h时,池中水量是多少?
5.某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆一次0.5元,一般车保管费是每辆一次0.3元.
(1)若一般车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3500辆自行车中,变速车的辆次不小于总辆次的25%,但不大于40%,试求该保管站这个星期日保管费收入总数的范围.
【拓展探究】
6.为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积/m2
单价/(万元/m2)
不超过30的部分
0.3
超过30不超过n(m2)
的部分(45≤n≤60)
0.5
超过n(m2)的部分
0.7
根据这个购房方案解决下列问题:
(1)若某三口之家欲购买120 m2的商品房,求其应缴纳的房款;
(2)设某三口之家购买商品房的人均面积为x m2,应缴纳房款为y万元,请写出y关于x的函数表达式.
【答案与解析】
1.C(解析:∵函数y=(m-5)x+(4m+1)x2中的y与x成正比例,∴即∴m=-.故选C.)
2.C (解析:①y=4x+3是一次函数;②y=x是一次函数;③y=x4的自变量的次数不为1,故不是一次函数;④y=x2的自变量的次数不为1,故不是一次函数;⑤y=1-x是一次函数.故选C.)
3.y=x(解析:只有y=x符合y=kx(k≠0)的形式.)
4.解:(1)Q=200+15t,0≤t≤40. (2)注水40 min可以把水池注满. (3)当注水0.2 h,即12 min时,池中水量为380 L.
5.解:(1)y与x的关系式是y=0.3x+0.5×(3500-x),即y=-0.2x+1750(0≤x≤3500,且x为整数). (2)因为变速车停放的辆次不小于3500的25%,但不大于3500的40%,所以一般自行车停放的辆次在3500×60%与3500×75%之间.当x=3500×60%=2100时,y=-0.2×2100+1750=1330;当x=3500×75%=2625时,y=-0.2×2625+1750=1225.所以该保管站这个星期日保管费收入总数在1225元至1330元之间.
6.解析:(1)根据房款=房屋单价×购房面积就可以表示出应缴房款.(2)分别求出当0≤x≤30,30n时y与x之间的表达式即可.解:(1)由题意,得应缴纳房款为0.3×90+0.5×30=42(万元). (2)由题意得:①0≤x≤30时,y=0.3×3x=0.9x;②30n时,y=0.3×90+0.5×3(n-30)+0.7×3×(x-n)=2.1x-18-0.6n.
教学时从学生熟悉的实际问题入手,旨在让学生通过直观感知领悟相关概念,通过学生的合作交流得到一次函数和正比例函数的定义,引导学生把新学习的函数知识与实际问题联系起来.
对正比例函数和一次函数之间的区别和联系没
有做重点强调,这对于学生以后画函数图象和分析图象、性质会带来一定的困难.
在教学过程中要适当增加习题,设计不同层次的习题,让不同层次的学生得到不同程度的练习,以提高学生的解题能力和对一次函数与正比例函数的理解和掌握.
随堂练习(教材第80页)
1.解:依题意得y=2.2x,所以y是x的一次函数,y也是x的正比例函数.
2.解:(1)y=80x+100,y是x的一次函数. (2)当x=0.5时,y=140.
习题4.2(教材第82页)
1.解:y=-3x.
2.解:(1)y=3x,y是x的一次函数, 也是x的正比例函数. (2)y=(10-2x)·x=-x2+5x,y不是x的一次函数,也不是x的正比例函数.
3.解:(1)y=12+0.2x. (2)48元. (3)440 min.
4.解:(1)y=0.25x. (2)45元. (3)400 min.
5.解:yA=0.2x+12,yB=0.25x.(1)当x=300时,yA=0.2×300+12=72,yB=0.25×300=75.因为yA要注意一次函数与正比例函数之间的关系,解决“根据所给条件写出简单的一次函数表达式”这类问题的基本思路为:先从实际问题中获取各种有用的信息,然后认真分析,探究这些有关的信息,在此基础上构建出数学模型,并解决这个数学问题,从而进一步解答问题.
如图所示,函数、一次函数和正比例函数之间的包含关系是 ( )
〔解析〕 正比例函数是一次函数的特殊形式,而它们又都是函数.故选A.
理解一次函数和正比例函数的概念,以及两者之间的关系,利用一次函数和正比例函数解决实际问题.
能够根据所给条件写出简单的一次函数表达式,并利用它解决实际问题.
1.通过函数与变量之间的联系,一次函数与一次方程的联系,提高学生的数学思维能力.
2.经历利用一次函数解决实际问题的过程,发展学生的数学应用能力.
【重点】
1.一次函数、正比例函数的概念.
2.一次函数、正比例函数的关系.
3.会根据已知信息写出一次函数的表达式.
【难点】 一次函数知识的运用.
【教师准备】 引例和例题投影图片.
【学生准备】 复习函数的定义、函数值等内容.
导入一:
生活中充满着许许多多变化的量,你了解这些变量之间的关系吗?如弹簧的长度(在弹性限度内)与所挂物体的质量,输液时间与相应时间内水滴数目……了解这些关系,可以帮助我们更好地认识世界.函数是刻画变量之间关系的常用模型,其中最为简单的是一次函数,那么什么是一次函数?用一次函数可以解决哪些问题呢?你想了解这些吗?一起进入这节课的学习吧!
导入二:
汽车的平均速度为95 km/h,A地直达北京的高速公路全程为570 km,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己与北京的距离.小明能得到一个什么样的关系式呢?他是怎样想的?猜猜看.
[过渡语] 怎样写出两个变量之间的函数关系式呢?
一、出示教材引例及问题
某弹簧的自然长度为3 cm.在弹性限度内,所挂物体的质量x每增加1 kg,弹簧长度y增加0.5 cm.
(1)计算所挂物体的质量分别为1 kg,2 kg,3 kg,4 kg,5 kg时弹簧的长度,并填入下表:
x/kg
0
1
2
3
4
5
y/cm
(2)你能写出y与x之间的关系式吗?
【分析】 当不挂物体时,弹簧长度为3厘米,当挂1千克物体时,增加0.5厘米,总长度为3.5厘米,增加1千克物体,即所挂物体为2千克时,弹簧又增加0.5厘米,总共增加1厘米,由此可见,所挂物体为x千克时,弹簧就伸长0.5x厘米,则弹簧总长为原长加伸长的长度,即y=3+0.5x.
二、做一做
某辆汽车油箱中原有汽油60 L,汽车每行驶50 km耗油6 L.
(1)完成下表:
汽车行驶
路程x/km
0
50
100
150
200
300
耗油量y/L
(2)你能写出耗油量y(L)与汽车行驶路程x(km)之间的关系式吗?
(3)你能写出油箱剩余油量z(L)与汽车行驶路程x(km)之间的关系式吗?
【答案与提示】 (1)如下表所示:
汽车行驶
路程x/km
0
50
100
150
200
300
耗油量y/L
0
6
12
18
24
36
(2)y=6·x.
(3)z=60-x.
【归纳】 若两个变量x,y间的对应关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数.例如y=2x+1, y=x-1等都是一次函数.
特别地,当b=0时,称y是x的正比例函数.例如,y=2x,y=-3x等都是正比例函数.
正比例函数是一次函数的特例,一次函数包含正比例函数.正比例函数与一次函数的关系如图所示.
[知识拓展] 正比例函数也是一次函数,不过是特殊的一次函数,就像是等边三角形与等腰三角形的关系一样.
三、例题讲解
写出下列各题中y与x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60 km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系;
(2)圆的面积y(cm2)与它的半径x(cm)之间的关系;
(3)某水池有水15 m3,现打开进水管进水,进水速度为5 m3/h,x h后这个水池内有水y m3.
(由学生交流讨论完成)
解:(1)由路程=速度×时间,得y=60x,y是x的一次函数,也是x的正比例函数.
(2)由圆的面积公式,得y=πx2,y不是x的正比例函数,也不是x的一次函数.
(3)这个水池每小时增加5 m3水,x h增加5x m3水,因而y=15+5x,y是x的一次函数,但不是x的正比例函数.
【思考】 两个变量之间存在函数关系,它们之间一定是一次函数或正比例函数关系吗?
我国自2011年9月1日起,个人工资、薪金所得税征收办法规定:月收入不超过3500元的部分不收税;月收入超过3500元但不超过5000元的部分征收3%的所得税……如某人月收入3860元,他应缴纳个人工资、薪金所得税为(3860-3500)×3%=10.8(元).
(1)当月收入超过3500元而又不超过5000元时,写出应缴纳个人工资、薪金所得税y(元)与月收入x(元)之间的关系式;
(2)某人月收入为4160元,他应缴纳个人工资、薪金所得税多少元?
(3)如果某人本月缴纳个人工资、薪金所得税19.2元,那么此人本月工资、薪金收入是多少元?
〔解析〕 一次函数y=kx+b(k,b为常数,k≠0)中,自变量的取值范围是全体实数,但是在实际问题中,要根据具体情况来确定该一次函数的自变量的取值范围.本例题的关键是确定问题当中的x的取值范围.
解:(1)当月收入超过3500元而不超过5000元时,
y=(x-3500)×3%,即y=0.03x-105.
(2)当x=4160时,y=0.03×4160-105=19.8(元)
(3)因为(5000-3500)×3%=45(元),19.2<45,所以此人本月工资、薪金收入不超过5000元.设此人本月工资、薪金收入是x元,则:
19.2=0.03x-105,x=4140.
即此人本月工资、薪金收入是4140元.
1.一根弹簧的原长为12 cm,它能挂的重量不能超过15 kg并且每挂重物1 kg就伸长0.5 cm,则在弹性限度内,挂重物后的弹簧长度y(cm)与所挂重物x(kg)之间的函数关系式是 .?
解析:弹簧伸长后的长度等于原长加上挂重物后伸长的长度,所以y=0.5x+12.由于这是实际问题,自变量的取值要有实际意义,所以0≤x≤15.故填y=0.5x+12(0≤x≤15).
2.y=kx+b是一次函数,则k为 ( )
A.一切实数 B.正实数
C.负实数 D.非零实数
解析:y=kx+b是一次函数,也就是说kx+b是关于x的一次式,所以k是不等于0的实数.故选D.
3.下列函数中,y是x的一次函数的是 ( )
A.y=-3x+5 B.y=-3x2
C.y= D.y=2
解析:形如y=kx+b(k,b为常数,k≠0)的函数是一次函数.故选A.
4.下列说法不正确的是 ( )
A.一次函数不一定是正比例函数
B.不是一次函数就一定不是正比例函数
C.正比例函数是特殊的一次函数
D.不是正比例函数就一定不是一次函数
解析:正比例函数是特殊的一次函数,不是正比例函数也可能是一次函数,如y=2x-3.故选D.
5.某面包厂现年产值是15万元,计划从今年开始每年增加产值2万元.
(1)写出年产值y(万元)与年数x之间的函数表达式;
(2)求5年后的年产值.
解析:(1)年产值等于现年产值加上每年增加的年产值乘年数.(2)将x=5代入(1)中求得的表达式即可得解.
解:(1)y=2x+15.
(2)当x=5时,y=2×5+15=25,
即5年后的年产值为25万元.
2 一次函数与正比例函数
1.出示教材引例及问题.
2.做一做.
3.例题讲解.
例1
例2
一、教材作业
【必做题】
教材第82页习题4.2第1,2题.
【选做题】
教材第82页习题4.2第5题.
二、课后作业
【基础巩固】
1.若函数y=(m-5)x+(4m+1)x2(m为常数)中的y与x成正比例,则m的取值范围为 ( )
A.m>- B.m> 5
C.m=- D.m=5
2.下列函数:①y=4x+3;②y=x;③y=x4;④y=x2;⑤y=1-x中,一次函数有 ( )
A.1个 B.2个 C.3个 D.4个
3.在函数y=x, y=x+3,y=,y=2x2-3, y=2(x-3)中, 是关于x的正比例函数.?
【能力提升】
4.容积为800 L的水池内已蓄水200 L,若每分钟注入的水量是15 L,设池内的水量为Q(L),注水时间为t(min).
(1)请写出Q与t的函数关系式;
(2)注水多长时间可以把水池注满?
(3)当注水时间为0. 2 h时,池中水量是多少?
5.某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆一次0.5元,一般车保管费是每辆一次0.3元.
(1)若一般车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3500辆自行车中,变速车的辆次不小于总辆次的25%,但不大于40%,试求该保管站这个星期日保管费收入总数的范围.
【拓展探究】
6.为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
人均住房面积/m2
单价/(万元/m2)
不超过30的部分
0.3
超过30不超过n(m2)
的部分(45≤n≤60)
0.5
超过n(m2)的部分
0.7
根据这个购房方案解决下列问题:
(1)若某三口之家欲购买120 m2的商品房,求其应缴纳的房款;
(2)设某三口之家购买商品房的人均面积为x m2,应缴纳房款为y万元,请写出y关于x的函数表达式.
【答案与解析】
1.C(解析:∵函数y=(m-5)x+(4m+1)x2中的y与x成正比例,∴即∴m=-.故选C.)
2.C (解析:①y=4x+3是一次函数;②y=x是一次函数;③y=x4的自变量的次数不为1,故不是一次函数;④y=x2的自变量的次数不为1,故不是一次函数;⑤y=1-x是一次函数.故选C.)
3.y=x(解析:只有y=x符合y=kx(k≠0)的形式.)
4.解:(1)Q=200+15t,0≤t≤40. (2)注水40 min可以把水池注满. (3)当注水0.2 h,即12 min时,池中水量为380 L.
5.解:(1)y与x的关系式是y=0.3x+0.5×(3500-x),即y=-0.2x+1750(0≤x≤3500,且x为整数). (2)因为变速车停放的辆次不小于3500的25%,但不大于3500的40%,所以一般自行车停放的辆次在3500×60%与3500×75%之间.当x=3500×60%=2100时,y=-0.2×2100+1750=1330;当x=3500×75%=2625时,y=-0.2×2625+1750=1225.所以该保管站这个星期日保管费收入总数在1225元至1330元之间.
6.解析:(1)根据房款=房屋单价×购房面积就可以表示出应缴房款.(2)分别求出当0≤x≤30,30
教学时从学生熟悉的实际问题入手,旨在让学生通过直观感知领悟相关概念,通过学生的合作交流得到一次函数和正比例函数的定义,引导学生把新学习的函数知识与实际问题联系起来.
对正比例函数和一次函数之间的区别和联系没
有做重点强调,这对于学生以后画函数图象和分析图象、性质会带来一定的困难.
在教学过程中要适当增加习题,设计不同层次的习题,让不同层次的学生得到不同程度的练习,以提高学生的解题能力和对一次函数与正比例函数的理解和掌握.
随堂练习(教材第80页)
1.解:依题意得y=2.2x,所以y是x的一次函数,y也是x的正比例函数.
2.解:(1)y=80x+100,y是x的一次函数. (2)当x=0.5时,y=140.
习题4.2(教材第82页)
1.解:y=-3x.
2.解:(1)y=3x,y是x的一次函数, 也是x的正比例函数. (2)y=(10-2x)·x=-x2+5x,y不是x的一次函数,也不是x的正比例函数.
3.解:(1)y=12+0.2x. (2)48元. (3)440 min.
4.解:(1)y=0.25x. (2)45元. (3)400 min.
5.解:yA=0.2x+12,yB=0.25x.(1)当x=300时,yA=0.2×300+12=72,yB=0.25×300=75.因为yA
如图所示,函数、一次函数和正比例函数之间的包含关系是 ( )
〔解析〕 正比例函数是一次函数的特殊形式,而它们又都是函数.故选A.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
