数学五年级上青岛版5.1 平行四边形的面积课件(29张)
文档属性
| 名称 | 数学五年级上青岛版5.1 平行四边形的面积课件(29张) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-23 00:00:00 | ||
图片预览



文档简介
课件29张PPT。梯形的面积回顾反思自主练习合作探索情境导入课后作业5 生活中的多边形——多边形的面积QD 五年级上册一、情境导入从图中,你知道了哪些数学信息?
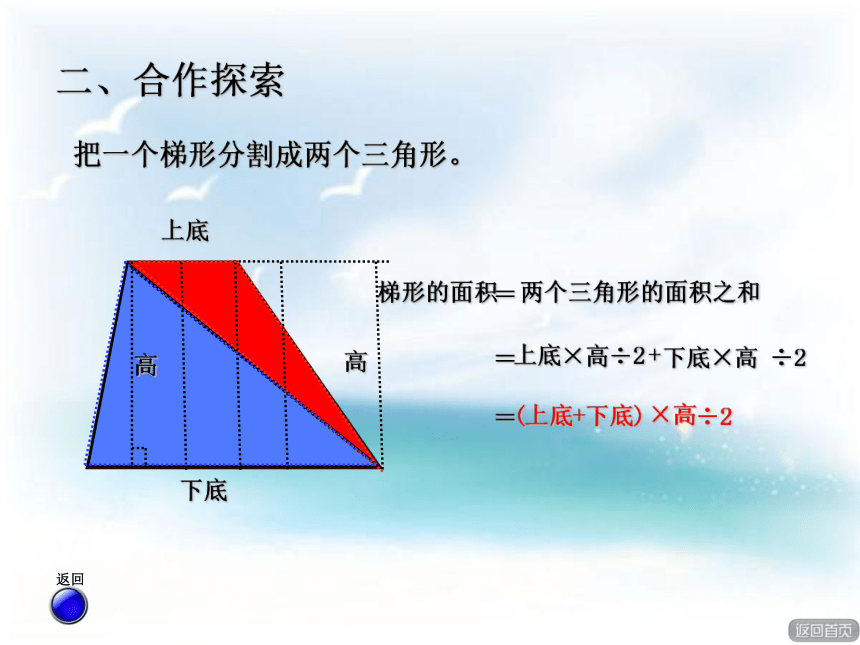
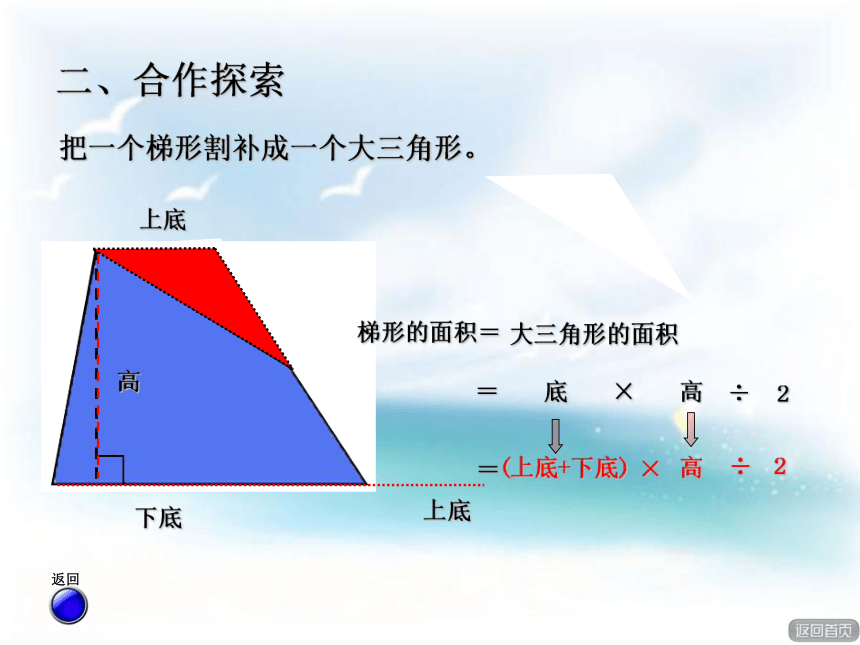
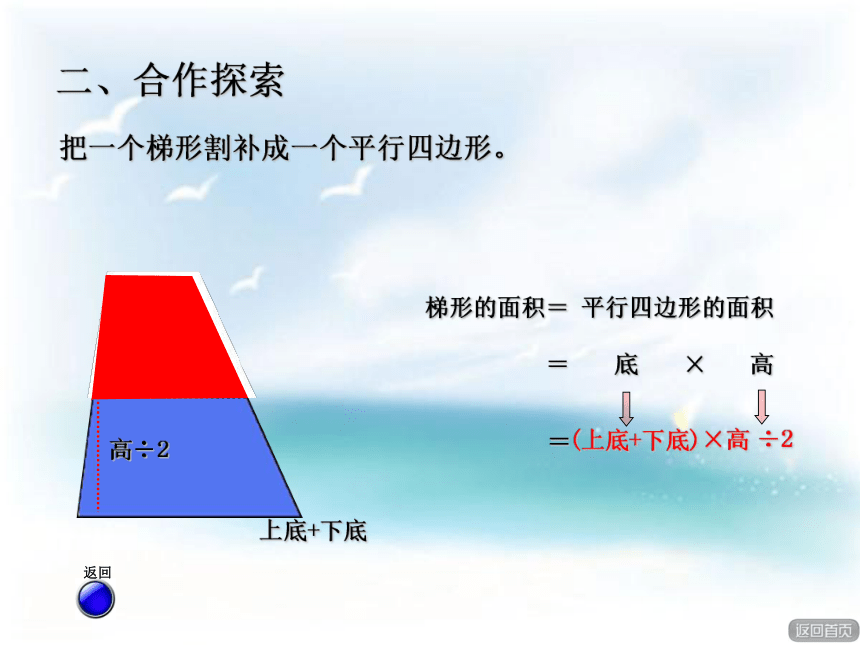
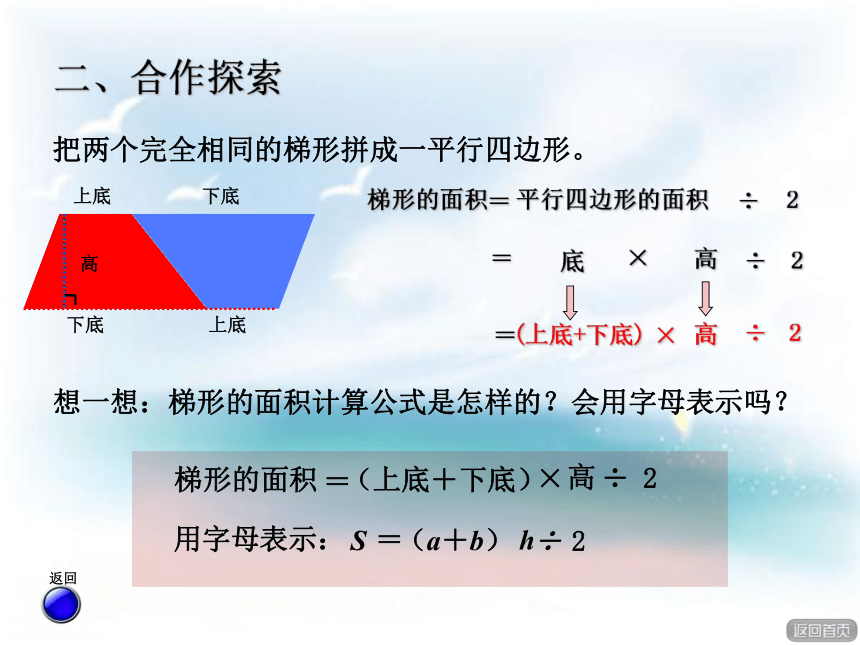
根据这些信息,你能提出什么问题?上底:32厘米下底:36厘米高: 32厘米制作这个椅子面需要多少平方厘米的木材?制作这个椅子面需要多少平方厘米的木材? 2个三角 1梯拼平 1个三角 2梯拼平继续1.想一想。求椅子面的面积,实际上就是求什么图形的面积?2.猜一猜。可以把梯形转化成什么图形来研究?会验证你的猜想吗?3.做一做。利用学具(两个完全相同的梯形)拼一拼,摆一摆,看看你有什么发现。探索活动要求 二、合作探索高上底下底上底×高÷2二、合作探索把一个梯形分割成两个三角形。 (上底+下底)下底×高 ÷2+÷2×高=梯形的面积两个三角形的面积之和==高二、合作探索上底下底上底梯形的面积==底×高(上底+下底)×=2高÷÷2大三角形的面积把一个梯形割补成一个大三角形。 高高÷2上底+下底二、合作探索梯形的面积= 平行四边形的面积=底×高(上底+下底)÷2×高=把一个梯形割补成一个平行四边形。 把两个完全相同的梯形拼成一平行四边形。 二、合作探索梯形的面积÷2平行四边形的面积=底×高(上底+下底)×=2高÷÷2=梯形的面积 = ×高÷2用字母表示: S(上底+下底)= (a+b)h÷2想一想:梯形的面积计算公式是怎样的?会用字母表示吗? (32+36)×32÷2二、合作探索制作这个椅子面需要多少平方厘米的木材? =68×32÷2=2176÷2=1088(平方厘米)答:制作这个椅子面需要1088平方厘米的木材。试一试1.想一想,填一填。
(1) 梯形的面积=( ),用字母表示是( )。
(2) 一个梯形的上底是5 cm,下底是9 cm,高是6 cm,两个这样的梯形拼成的平行四边形的一个底是( ) cm,该底上的高是( )cm。
(3) 一个梯形的上底增加3 cm,下底减少3 cm,高不变,面积( )(填“变大”“变小”或“不变”)。二、合作探索(上底+下底)×高÷2S=(a+b)h÷2614不变2.求下面梯形的面积。(单位: cm)
(1)
(2) 二、合作探索(5+11)×4÷2=32(cm2)(7+11)×5÷2=45(cm2)3.解决下列问题。
(1) 一条水渠的横截面是一个梯形,渠口宽2.2 m,渠底宽1.4 m,渠深1.5 m。它的横截面的面积是多少平方米?二、合作探索(2.2+1.4)×1.5÷2=2.7(m2)
答:它的横截面的面积是2.7 m2。(2) 一块橘子园的地面形状是梯形,它的上底是120米,下底是160米,高是50米。如果每棵橘子树占地10平方米,这块地种了多少棵橘子树?二、合作探索(120+160)×50÷2÷10=700(棵)
答:这块地种了700棵橘子树。(3) 一块梯形土地的面积是45平方米,下底是10米,上底是5米,它的高是多少米?二、合作探索45×2÷(10+5)=6(米)
答:它的高是6米。(4) 用篱笆靠墙围成一个梯形的养鸭场,如下图,篱笆长58米,求养鸭场的面积。二、合作探索(58-15)×15÷2=322.5(平方米)
答:养鸭场的面积是322.5平方米。(5) 如图,算一算这堆圆木一共有多少根?二、合作探索(1+8)×8÷2=36(根)
答:这堆圆木一共有36根。二、合作探索拓展:
1. 已知梯形的面积、上底和下底,求它的高,既可以用公式直接列方程求解,也可以用算术法解答。由梯形的面积计算公式可推导出:梯形的高=面积×2÷(上底+下底)用字母表示是:h=2S÷(a+b)。
已知梯形的面积、上底(或下底)和高,求它的下底(或上底),既可以用公式直接列方程求解,也可以用算术法解答。由梯形的面积计算公式可推导出:梯形的下底=面积×2÷高-上底,用字母表示b=2S÷h-a。同理:梯形的上底=面积×2÷高-下底,用字母表示是a =2S÷h-b。二、合作探索梯形面积的计算,转化图形最关键。
拼摆分割与推导,计算公式现眼前。
上下底之和乘高,再除以2莫忘了。
利用公式巧计算,解决问题不为难。?计算下面图形的面积。试一试 (17+23)×15÷2=40×15÷2=300(m2)
(18+9)×10÷2=27×10÷2=135(dm2)
1.任选一个图形计算它的面积(图中单位:厘米) (7.5+12.5)×11÷2三、自主练习 (42+26)×30÷2=68×30÷2=1020(平方厘米)
=20×11÷2=110(平方厘米)
2.选择正确的列式(1) (13+10)×8.5÷2(3) (13+10) ×12.5÷2(2) (8.5+12.5) ×13÷2(4) (8.5+12.5) ×10÷2√三、自主练习三、自主练习3. (8+5)×1.8÷2某水渠的横截面是梯形(如图)渠口宽8米。渠底宽5米,渠深1.8米。求它的横截面面积。= 13×1.8÷2= 11.7(平方米)答:它的横截面面积是11.7平方米。三、自主练习4. (40+60)×30÷2×10= 100×30÷2×10= 1500(cm2)做10件这样的围裙,大约用多少平方米布?答:做10件这样的围裙,大约用0.15平方米布。1500cm2=0.15m2 (3+7)×5÷25.木材场常常把木材堆成下图形状。试算出图中木材的根数,并用梯形的面积公式解释算法。三、自主练习= 10×5÷2= 25(根)答:这堆木材共有25根。(3+6)×7 ÷2= 9×7 ÷2= 31.5(cm2)如果几个梯形等底等高,那么它们的面积一定相等。三、自主练习6.计算下面每个梯形的面积,你发现了什么?(单位:cm)三、自主练习7.在方格纸上画出面积是6平方厘米、形状不同的梯形,并验证。1cm2 (2+4)×2÷2 = 6×2÷2 = 6(cm2) (1+2)×4÷2 = 3×4÷2 = 6(cm2) (1+5)×2÷2 = 6×2÷2 = 6(cm2) (1+3)×3÷2 = 4×3÷2 = 6(cm2)三、自主练习易错辨析 4.判断。(对的画“√”,错的画“×”)
(1)两个面积相等的梯形,一定能拼成一个平行四边形。( )
(2)平行四边形的面积一定比梯形的面积大。 ( )
(3) 求左图的面积应列式为(4+6)×3.6÷2。 ( )
(4)把一个平行四边形任意分割成两个梯形,这两个梯形的高总是相等的。 ( )×解析:弄清楚“两个面积相等的图形”与“两个完全相同的图形”的区别。√××四、回顾反思五、课后作业作 业 请完成教材第74~75页“自主练习”第1(剩余的题目)、4、6、聪明小屋题。
根据这些信息,你能提出什么问题?上底:32厘米下底:36厘米高: 32厘米制作这个椅子面需要多少平方厘米的木材?制作这个椅子面需要多少平方厘米的木材? 2个三角 1梯拼平 1个三角 2梯拼平继续1.想一想。求椅子面的面积,实际上就是求什么图形的面积?2.猜一猜。可以把梯形转化成什么图形来研究?会验证你的猜想吗?3.做一做。利用学具(两个完全相同的梯形)拼一拼,摆一摆,看看你有什么发现。探索活动要求 二、合作探索高上底下底上底×高÷2二、合作探索把一个梯形分割成两个三角形。 (上底+下底)下底×高 ÷2+÷2×高=梯形的面积两个三角形的面积之和==高二、合作探索上底下底上底梯形的面积==底×高(上底+下底)×=2高÷÷2大三角形的面积把一个梯形割补成一个大三角形。 高高÷2上底+下底二、合作探索梯形的面积= 平行四边形的面积=底×高(上底+下底)÷2×高=把一个梯形割补成一个平行四边形。 把两个完全相同的梯形拼成一平行四边形。 二、合作探索梯形的面积÷2平行四边形的面积=底×高(上底+下底)×=2高÷÷2=梯形的面积 = ×高÷2用字母表示: S(上底+下底)= (a+b)h÷2想一想:梯形的面积计算公式是怎样的?会用字母表示吗? (32+36)×32÷2二、合作探索制作这个椅子面需要多少平方厘米的木材? =68×32÷2=2176÷2=1088(平方厘米)答:制作这个椅子面需要1088平方厘米的木材。试一试1.想一想,填一填。
(1) 梯形的面积=( ),用字母表示是( )。
(2) 一个梯形的上底是5 cm,下底是9 cm,高是6 cm,两个这样的梯形拼成的平行四边形的一个底是( ) cm,该底上的高是( )cm。
(3) 一个梯形的上底增加3 cm,下底减少3 cm,高不变,面积( )(填“变大”“变小”或“不变”)。二、合作探索(上底+下底)×高÷2S=(a+b)h÷2614不变2.求下面梯形的面积。(单位: cm)
(1)
(2) 二、合作探索(5+11)×4÷2=32(cm2)(7+11)×5÷2=45(cm2)3.解决下列问题。
(1) 一条水渠的横截面是一个梯形,渠口宽2.2 m,渠底宽1.4 m,渠深1.5 m。它的横截面的面积是多少平方米?二、合作探索(2.2+1.4)×1.5÷2=2.7(m2)
答:它的横截面的面积是2.7 m2。(2) 一块橘子园的地面形状是梯形,它的上底是120米,下底是160米,高是50米。如果每棵橘子树占地10平方米,这块地种了多少棵橘子树?二、合作探索(120+160)×50÷2÷10=700(棵)
答:这块地种了700棵橘子树。(3) 一块梯形土地的面积是45平方米,下底是10米,上底是5米,它的高是多少米?二、合作探索45×2÷(10+5)=6(米)
答:它的高是6米。(4) 用篱笆靠墙围成一个梯形的养鸭场,如下图,篱笆长58米,求养鸭场的面积。二、合作探索(58-15)×15÷2=322.5(平方米)
答:养鸭场的面积是322.5平方米。(5) 如图,算一算这堆圆木一共有多少根?二、合作探索(1+8)×8÷2=36(根)
答:这堆圆木一共有36根。二、合作探索拓展:
1. 已知梯形的面积、上底和下底,求它的高,既可以用公式直接列方程求解,也可以用算术法解答。由梯形的面积计算公式可推导出:梯形的高=面积×2÷(上底+下底)用字母表示是:h=2S÷(a+b)。
已知梯形的面积、上底(或下底)和高,求它的下底(或上底),既可以用公式直接列方程求解,也可以用算术法解答。由梯形的面积计算公式可推导出:梯形的下底=面积×2÷高-上底,用字母表示b=2S÷h-a。同理:梯形的上底=面积×2÷高-下底,用字母表示是a =2S÷h-b。二、合作探索梯形面积的计算,转化图形最关键。
拼摆分割与推导,计算公式现眼前。
上下底之和乘高,再除以2莫忘了。
利用公式巧计算,解决问题不为难。?计算下面图形的面积。试一试 (17+23)×15÷2=40×15÷2=300(m2)
(18+9)×10÷2=27×10÷2=135(dm2)
1.任选一个图形计算它的面积(图中单位:厘米) (7.5+12.5)×11÷2三、自主练习 (42+26)×30÷2=68×30÷2=1020(平方厘米)
=20×11÷2=110(平方厘米)
2.选择正确的列式(1) (13+10)×8.5÷2(3) (13+10) ×12.5÷2(2) (8.5+12.5) ×13÷2(4) (8.5+12.5) ×10÷2√三、自主练习三、自主练习3. (8+5)×1.8÷2某水渠的横截面是梯形(如图)渠口宽8米。渠底宽5米,渠深1.8米。求它的横截面面积。= 13×1.8÷2= 11.7(平方米)答:它的横截面面积是11.7平方米。三、自主练习4. (40+60)×30÷2×10= 100×30÷2×10= 1500(cm2)做10件这样的围裙,大约用多少平方米布?答:做10件这样的围裙,大约用0.15平方米布。1500cm2=0.15m2 (3+7)×5÷25.木材场常常把木材堆成下图形状。试算出图中木材的根数,并用梯形的面积公式解释算法。三、自主练习= 10×5÷2= 25(根)答:这堆木材共有25根。(3+6)×7 ÷2= 9×7 ÷2= 31.5(cm2)如果几个梯形等底等高,那么它们的面积一定相等。三、自主练习6.计算下面每个梯形的面积,你发现了什么?(单位:cm)三、自主练习7.在方格纸上画出面积是6平方厘米、形状不同的梯形,并验证。1cm2 (2+4)×2÷2 = 6×2÷2 = 6(cm2) (1+2)×4÷2 = 3×4÷2 = 6(cm2) (1+5)×2÷2 = 6×2÷2 = 6(cm2) (1+3)×3÷2 = 4×3÷2 = 6(cm2)三、自主练习易错辨析 4.判断。(对的画“√”,错的画“×”)
(1)两个面积相等的梯形,一定能拼成一个平行四边形。( )
(2)平行四边形的面积一定比梯形的面积大。 ( )
(3) 求左图的面积应列式为(4+6)×3.6÷2。 ( )
(4)把一个平行四边形任意分割成两个梯形,这两个梯形的高总是相等的。 ( )×解析:弄清楚“两个面积相等的图形”与“两个完全相同的图形”的区别。√××四、回顾反思五、课后作业作 业 请完成教材第74~75页“自主练习”第1(剩余的题目)、4、6、聪明小屋题。
