14.2-3 乘法公式与因式分解培优提高试题
文档属性
| 名称 | 14.2-3 乘法公式与因式分解培优提高试题 |

|
|
| 格式 | doc | ||
| 文件大小 | 408.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-26 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
八上数学第十四章培优提高 第2-3节 乘法公式与因式分解
一.选择题(共10小题)
1.下列多项式乘法中,可以用平方差公式计算的是( )
A.(x+1)(1+x) B.(a+b)(b﹣a) C.(﹣a+b)(a﹣b) D.(x2﹣y)(x+y2)
2.下列多项式中,a2﹣4a+4,1+4a2,4b2+4b﹣1,a2+ab+b2.完全平方式有( )个.
A.1个 B.2个 C.3个 D.4个
3.下列等式从左到右的变形是因式分解的是( )
A.6a2b=3a 2ab B.(x+4)(x﹣4)=x2﹣16【来源:21·世纪·教育·网】
C.2ax﹣2ay=2a(x﹣y) D.4x2+8x﹣1=4x(x+2)﹣1
4.已知mn=1,m﹣n=2,则m2n﹣mn2的值是( )
A.﹣1 B.3 C.2 D.﹣2www-2-1-cnjy-com
5.下列各式成立的是( )
A.a﹣(b+c)=a﹣b+c B.a+b﹣c=a+(b﹣c)
C.a+(b+c)=a﹣b+c D.a+b﹣c=a﹣(b+c)
6.将面积为a2的正方形边长增加3,则正方形的面积增加了( )
A.9 B.2a+9 C.3a+9 D.6a+92-1-c-n-j-y
7.三个连续奇数,若中间一个为n,则它们的积是( )
A.6n3﹣6n B.4n3﹣n C.n3﹣4n D.n3﹣n21*cnjy*com
8.如果x2﹣mx+36是一个完全平方式,则m的值为( )
A.6 B.12 C.±6 D.±1221·世纪*教育网
9.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a﹣1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
A.2 cm2 B.2a cm2 C.4a cm2 D.(a2﹣1)cm2
10.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分面积,可以验证下面一个等式是( )
A.(a+b)2=a2+2ab+b2 B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b) D.a2+b2=[(a+b)2+(a﹣b)2]
二.填空题(共8小题)
11.已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值为 .
12.已知a+b=10,a﹣b=8,则a2﹣b2= .
13.把多项式x2+4mx+5因式分解得(x+5)(x+n),则m+n的值为 .
14.已知:2x2﹣4xy+4y2+6x+9=0,则x+y= .
15.在实数范围内分解因式:x4﹣9= .
16.分解因式:(x2+x+1)(x2+x+2)﹣12=
17.把x2y2+4加上一个单项式,使其成为多项式的完全平方式,请你写出所有符合条件的单项式 .【来源:21cnj*y.co*m】
18.完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数 .【出处:21教育名师】
三.解答题(共9小题)
19.计算:
(1)(2x+3y)2﹣(4x﹣9y)(4x+9y)+(3x﹣2y)2.
(2)(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b)
20.分解因式:
(1)x4﹣81; (2)3x3﹣12xy2; (3)4(x+y)2﹣1;
(4)(x2+x+1)2﹣1; (5)9(x+y)2﹣4(x﹣y)2.
21.给出三个多项式:x2+x﹣1,x2+3x+1,x2﹣x,请你写出其中两个多项式的加法运算,并把运算结果因式分解.21cnjy.com
22.化简求值
(1)先化简,再求值:(x+y)(x﹣y)﹣x(x+y)+2xy,其中x=1,y=2.
(2)化简求值:(a+b)2﹣2a(b+1)﹣a2b÷b,其中a=﹣2,b=2.
23.基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2﹣x﹣2=0可通过因式分解化为(x﹣2)(x+1)=0,由基本事实得x﹣2=0或x+1=0,即方程的解为x=2或x=﹣1.
(1)试利用上述基本事实,解方程:2x2﹣x=0:
(2)解方程:(x+1)(x+2)+=0.
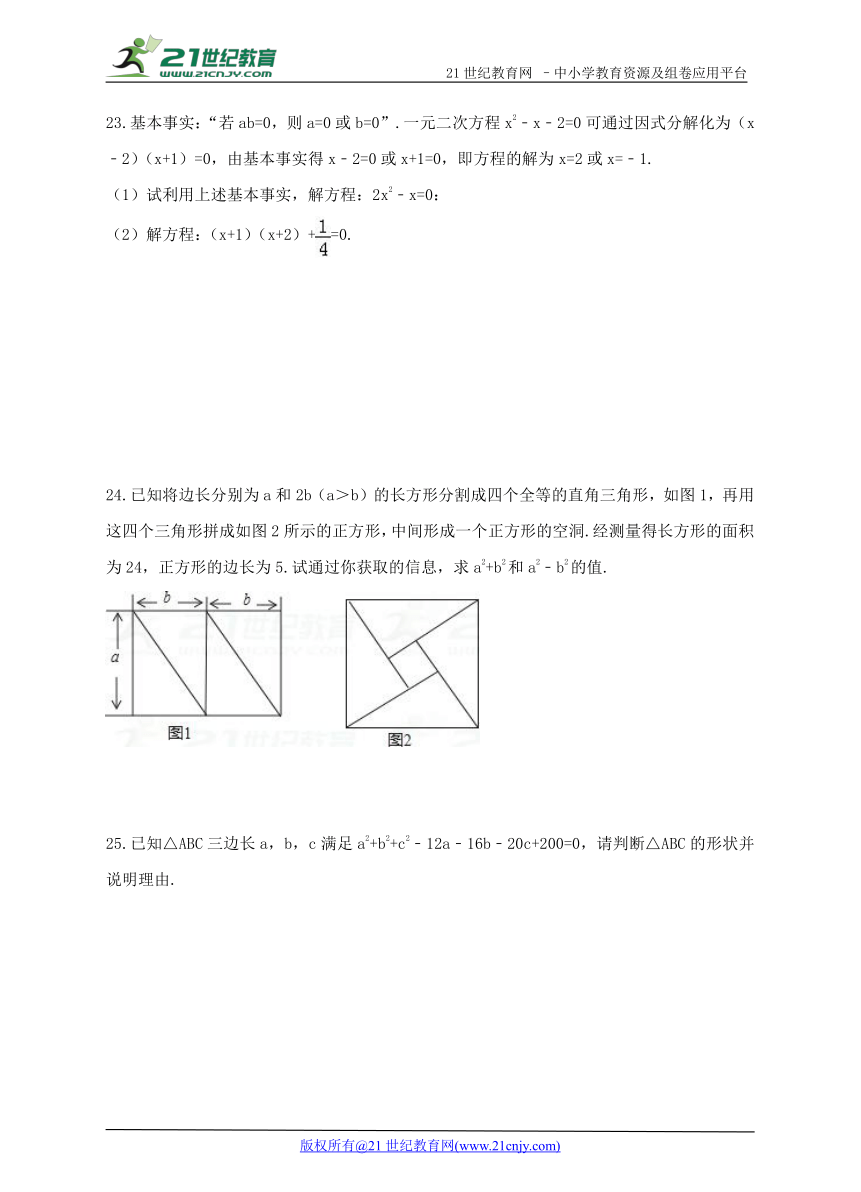
24.已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
25.已知△ABC三边长a,b,c满足a2+b2+c2﹣12a﹣16b﹣20c+200=0,请判断△ABC的形状并说明理由.21世纪教育网版权所有
26.如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,则说明4,12,20都是神秘数.21·cn·jy·com
(1)28和2012是神秘数吗?为什么?
(2)设两个连续偶数为2k和2k+2(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?
(3)两个连续奇数(取正整数)的平方差是神秘数吗?为什么?
27.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).2·1·c·n·j·y
(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
八上数学第十四章培优提高 第2-3节 乘法公式与因式分解
参考答案与试题解析
一.选择题(共10小题)
1B.【解答】解:A、不存在互为相反数的项,故本选项错误;
B、b是相同的项,互为相反项是a与﹣a,正确;
C、(﹣a+b)(a﹣b)=﹣(a﹣b)(a﹣b),不符合平方差公式的特点;
D、不存在相同的项,故本选项错误.故选B.
2A.【解答】解:a2﹣4a+4=(a﹣2)2,而1+4a2,4b2+4b﹣1,a2+ab+b2都不是完全平方式,
则完全平方式有1个.故选A.
3C.【解答】解:A、6a2b=3a 2ab,不符合因式分解的定义,故此选项错误;
B、(x+4)(x﹣4)=x2﹣16,是整式的乘法运算,故此选项错误;
C、2ax﹣2ay=2a(x﹣y),是因式分解,故此选项正确;
D、4x2+8x﹣1=4x(x+2)﹣1,不符合因式分解的定义,故此选项错误;故选:C.
4C.【解答】解:m2n﹣mn2=mn(m﹣n),∵mn=1,m﹣n=2,∴原式=1×2=2,故选C.
5B.【解答】解:A、a﹣(b+c)=a﹣b﹣c,故本选项错误;
B、a+b﹣c=a+(b﹣c),故本选项正确;
C、a+(b+c)=a+b+c,故本选项错误;
D、a+b﹣c=a﹣(﹣b+c),故本选项错误;故选B.
6D.【解答】解:∵面积为a2的正方形,∴其边长为:a,
∵正方形边长增加3,∴正方形的面积增加了:(a+3)2﹣a2=6a+9.故选:D.
7C.【解答】解:设中间的数为n,那么最小的奇数是n﹣2,最大的奇数是n+2,那么有:
(n﹣2)×n(n+2)=n3﹣4n.故选C.
8D.【解答】解:∵x2﹣mx+36是一个完全平方式,∴m=±12.故选D
9C.【解答】解:矩形的面积是:(a+1)2﹣(a﹣1)2=4a(cm2).故选:C.
10C.【解答】解:∵左图中阴影部分的面积是a2﹣b2,右图中梯形的面积是
(2a+2b)(a﹣b)=(a+b)(a﹣b),∴a2﹣b2=(a+b)(a﹣b).故选C.
二.填空题(共8小题)
11. ﹣1 .
【解答】解:原式=b+c﹣a+d=c+d﹣a+b=(c+d)﹣(a﹣b)=2﹣3=﹣1.
12. 80 .
【解答】解:∵(a+b)(a﹣b)=a2﹣b2,∴a2﹣b2=10×8=80,故答案为:80
13. .
【解答】解:由x2+4mx+5因式分解得(x+5)(x+n),得
x2+4mx+5=(x+5)(x+n),(x+5)(x+n)=x2+(n+5)x+5n,
x2+4mx+5=x2+(n+5)x+5n.4m=n+5,5n=5.解得n=1,m=
m+n=1+=,故答案为:.
14. .
【解答】解:由已知等式,得(x﹣2y)2+(x+3)2=0,
根据非负数的性质,得x﹣2y=0,x+3=0,解得x=﹣3,y=﹣,
∴x+y=﹣3﹣=﹣.故答案为:﹣.
15. (x﹣)(x+)(x2+3) .
【解答】解:x4﹣9=(x2)2﹣32=(x2﹣3)(x2+3)=(x﹣)(x+)(x2+3).
故答案为:(x﹣)(x+)(x2+3).
16. (x2+x+5)(x+2)(x﹣1) .
【解答】解:原式=(x2+x)2+3(x2+x)﹣10=(x2+x+5)(x2+x﹣2)=(x2+x+5)(x+2)(x﹣1).
故答案为:(x2+x+5)(x+2)(x﹣1).
17. ±4xy、 .
【解答】解:∵x2y2+4±4xy=(xy±2)2;
x2y2+4+=(+2)2;∴加上的单项式可以是±4xy、中任意一个.
故答案为:±4xy、.
18. 21 .
【解答】解:由图中的规律可知:上面两个数之和就是下面的一行的数;
∴第7行的数是:1 7 21 35 35 21 7 1
故(a+b)7展开后从左向右第三项的系数是21故答案为:21
三.解答题(共9小题)
19.【解答】解:(1)原式=4x2+9y2+12xy﹣16x2+81y2+9x2+4y2﹣12xy=﹣3x2+94y2;
(2)原式=a2﹣4ab+4b2﹣b2+4a2﹣4a2+4ab=a2+3b2.
20.【解答】解:(1)原式=(x2+9)(x2﹣9)=(x2+9)(x+3)(x﹣3);
(2)原式=3x(x2﹣4y2)=3x(x+2y)(x﹣2y);
(3)原式=(2x+2y+1)(2x+2y﹣1);
(4)原式=(x2+x+1+1)(x2+x+1﹣1)=(x2+x+2)(x2+x);
(5)原式=[3(x+y)+2(x﹣y)][3(x+y)﹣2(x﹣y)]=(5x+y)(x+5y).
21.【解答】解:分三种情况:
①(x2+x﹣1)+(x2+3x+1)=x2+x﹣1+x2+3x+1=x2+4x=x(x+4);
②(x2+x﹣1)+(x2﹣x)=x2+x﹣1+x2﹣x=x2﹣1=(x+1)(x﹣1);
③(x2+3x+1)+(x2﹣x)=x2+3x+1+x2﹣x=x2+2x+1=(x+1)2.
22.【解答】解:(1)原式=x2﹣y2﹣x2﹣xy+2xy=﹣y2+xy
将x=1,y=2代入得:原式=﹣2;
(2)原式=a2+2ab+b2﹣2ab﹣2a﹣a2=b2﹣2a,
将a=﹣2,b=2代入得:原式=8.
23.【解答】解:(1)方程左边因式分解可得:x(2x﹣1)=0,∴x=0或2x﹣1=0,
解得:x=0或x=;
(2)原方程整理可得:x2+3x+=0,
左边因式分解可得:(x+)2=0,∴x+=0,解得:x=﹣.
24.【解答】解:根据题意得a2+b2=52=25,a 2b=24,∴a2+b2+2ab49,
∴a+b=7,∵a>b,∴a=4,b=3,∴a2+b2=25,a2﹣b2=7.
25.【解答】解:△ABC为直角三角形
理由:∵a2+b2+c2﹣12a﹣16b﹣20c+200
=a2﹣12a+36+b2﹣16b+64+c2﹣20c+100
=(a﹣6)2+(b﹣8)2+(c﹣10)2=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,∴a=6,b=8,c=10,
∴a2+b2=36+64=100=c2∴△ABC为直角三角形.
26.【解答】解:(1)∵28=82﹣62,2012=5042﹣5022,
∴28是“神秘数”;2012是“神秘数”;
(2)两个连续偶数构成的“神秘数”是4的倍数.理由如下:
(2k+2)2﹣(2k)2=(2k+2+2k)(2k+2﹣2k)=2(4k+2)=4(2k+1),
∴两个连续偶数构成的“神秘数”是4的倍数,
∵2k+1是奇数,∴它是4的倍数,不是8的倍数;
(3)设两个连续的奇数为:2k+1,2k﹣1,则
(2k+1)2﹣(2k﹣1)2=8k,
此数是8的倍数,而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
27.【解答】解:(1)阴影部分为边长为(b﹣a)的正方形,所以阴影部分的面积(b﹣a)2,
故答案为:(b﹣a)2;
(2)图2中,用边长为a+b的正方形的面积减去边长为b﹣a的正方形等于4个长宽分别a、b的矩形面积,所以(a+b)2﹣(a﹣b)2=4ab,21教育网
故答案为:(a+b)2﹣(a﹣b)2=4ab;
(3)∵(x+y)2﹣(x﹣y)2=4xy,而x+y=7,x y=,
∴72﹣(x﹣y)2=4×,∴(x﹣y)2=4,∴x﹣y=±2,
故答案为:±2;
(4)边长为(a+b)与(3a+b)的矩形面积为(a+b)(3a+b),它由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,www.21-cn-jy.com
∴3a2+4ab+b2=(a+b) (3a+b),
故答案为:3a2+4ab+b2=(a+b) (3a+b).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
八上数学第十四章培优提高 第2-3节 乘法公式与因式分解
一.选择题(共10小题)
1.下列多项式乘法中,可以用平方差公式计算的是( )
A.(x+1)(1+x) B.(a+b)(b﹣a) C.(﹣a+b)(a﹣b) D.(x2﹣y)(x+y2)
2.下列多项式中,a2﹣4a+4,1+4a2,4b2+4b﹣1,a2+ab+b2.完全平方式有( )个.
A.1个 B.2个 C.3个 D.4个
3.下列等式从左到右的变形是因式分解的是( )
A.6a2b=3a 2ab B.(x+4)(x﹣4)=x2﹣16【来源:21·世纪·教育·网】
C.2ax﹣2ay=2a(x﹣y) D.4x2+8x﹣1=4x(x+2)﹣1
4.已知mn=1,m﹣n=2,则m2n﹣mn2的值是( )
A.﹣1 B.3 C.2 D.﹣2www-2-1-cnjy-com
5.下列各式成立的是( )
A.a﹣(b+c)=a﹣b+c B.a+b﹣c=a+(b﹣c)
C.a+(b+c)=a﹣b+c D.a+b﹣c=a﹣(b+c)
6.将面积为a2的正方形边长增加3,则正方形的面积增加了( )
A.9 B.2a+9 C.3a+9 D.6a+92-1-c-n-j-y
7.三个连续奇数,若中间一个为n,则它们的积是( )
A.6n3﹣6n B.4n3﹣n C.n3﹣4n D.n3﹣n21*cnjy*com
8.如果x2﹣mx+36是一个完全平方式,则m的值为( )
A.6 B.12 C.±6 D.±1221·世纪*教育网
9.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a﹣1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )
A.2 cm2 B.2a cm2 C.4a cm2 D.(a2﹣1)cm2
10.如图,在边长为a的正方形中剪去一个边长为b的小正方形(a>b),把剩下的部分拼成一个梯形,分别计算这两个图形阴影部分面积,可以验证下面一个等式是( )
A.(a+b)2=a2+2ab+b2 B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b) D.a2+b2=[(a+b)2+(a﹣b)2]
二.填空题(共8小题)
11.已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值为 .
12.已知a+b=10,a﹣b=8,则a2﹣b2= .
13.把多项式x2+4mx+5因式分解得(x+5)(x+n),则m+n的值为 .
14.已知:2x2﹣4xy+4y2+6x+9=0,则x+y= .
15.在实数范围内分解因式:x4﹣9= .
16.分解因式:(x2+x+1)(x2+x+2)﹣12=
17.把x2y2+4加上一个单项式,使其成为多项式的完全平方式,请你写出所有符合条件的单项式 .【来源:21cnj*y.co*m】
18.完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数 .【出处:21教育名师】
三.解答题(共9小题)
19.计算:
(1)(2x+3y)2﹣(4x﹣9y)(4x+9y)+(3x﹣2y)2.
(2)(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b)
20.分解因式:
(1)x4﹣81; (2)3x3﹣12xy2; (3)4(x+y)2﹣1;
(4)(x2+x+1)2﹣1; (5)9(x+y)2﹣4(x﹣y)2.
21.给出三个多项式:x2+x﹣1,x2+3x+1,x2﹣x,请你写出其中两个多项式的加法运算,并把运算结果因式分解.21cnjy.com
22.化简求值
(1)先化简,再求值:(x+y)(x﹣y)﹣x(x+y)+2xy,其中x=1,y=2.
(2)化简求值:(a+b)2﹣2a(b+1)﹣a2b÷b,其中a=﹣2,b=2.
23.基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2﹣x﹣2=0可通过因式分解化为(x﹣2)(x+1)=0,由基本事实得x﹣2=0或x+1=0,即方程的解为x=2或x=﹣1.
(1)试利用上述基本事实,解方程:2x2﹣x=0:
(2)解方程:(x+1)(x+2)+=0.
24.已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
25.已知△ABC三边长a,b,c满足a2+b2+c2﹣12a﹣16b﹣20c+200=0,请判断△ABC的形状并说明理由.21世纪教育网版权所有
26.如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,则说明4,12,20都是神秘数.21·cn·jy·com
(1)28和2012是神秘数吗?为什么?
(2)设两个连续偶数为2k和2k+2(k为非负整数),由这两个连续偶数构成的神秘数是4的倍数吗?
(3)两个连续奇数(取正整数)的平方差是神秘数吗?为什么?
27.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).2·1·c·n·j·y
(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
八上数学第十四章培优提高 第2-3节 乘法公式与因式分解
参考答案与试题解析
一.选择题(共10小题)
1B.【解答】解:A、不存在互为相反数的项,故本选项错误;
B、b是相同的项,互为相反项是a与﹣a,正确;
C、(﹣a+b)(a﹣b)=﹣(a﹣b)(a﹣b),不符合平方差公式的特点;
D、不存在相同的项,故本选项错误.故选B.
2A.【解答】解:a2﹣4a+4=(a﹣2)2,而1+4a2,4b2+4b﹣1,a2+ab+b2都不是完全平方式,
则完全平方式有1个.故选A.
3C.【解答】解:A、6a2b=3a 2ab,不符合因式分解的定义,故此选项错误;
B、(x+4)(x﹣4)=x2﹣16,是整式的乘法运算,故此选项错误;
C、2ax﹣2ay=2a(x﹣y),是因式分解,故此选项正确;
D、4x2+8x﹣1=4x(x+2)﹣1,不符合因式分解的定义,故此选项错误;故选:C.
4C.【解答】解:m2n﹣mn2=mn(m﹣n),∵mn=1,m﹣n=2,∴原式=1×2=2,故选C.
5B.【解答】解:A、a﹣(b+c)=a﹣b﹣c,故本选项错误;
B、a+b﹣c=a+(b﹣c),故本选项正确;
C、a+(b+c)=a+b+c,故本选项错误;
D、a+b﹣c=a﹣(﹣b+c),故本选项错误;故选B.
6D.【解答】解:∵面积为a2的正方形,∴其边长为:a,
∵正方形边长增加3,∴正方形的面积增加了:(a+3)2﹣a2=6a+9.故选:D.
7C.【解答】解:设中间的数为n,那么最小的奇数是n﹣2,最大的奇数是n+2,那么有:
(n﹣2)×n(n+2)=n3﹣4n.故选C.
8D.【解答】解:∵x2﹣mx+36是一个完全平方式,∴m=±12.故选D
9C.【解答】解:矩形的面积是:(a+1)2﹣(a﹣1)2=4a(cm2).故选:C.
10C.【解答】解:∵左图中阴影部分的面积是a2﹣b2,右图中梯形的面积是
(2a+2b)(a﹣b)=(a+b)(a﹣b),∴a2﹣b2=(a+b)(a﹣b).故选C.
二.填空题(共8小题)
11. ﹣1 .
【解答】解:原式=b+c﹣a+d=c+d﹣a+b=(c+d)﹣(a﹣b)=2﹣3=﹣1.
12. 80 .
【解答】解:∵(a+b)(a﹣b)=a2﹣b2,∴a2﹣b2=10×8=80,故答案为:80
13. .
【解答】解:由x2+4mx+5因式分解得(x+5)(x+n),得
x2+4mx+5=(x+5)(x+n),(x+5)(x+n)=x2+(n+5)x+5n,
x2+4mx+5=x2+(n+5)x+5n.4m=n+5,5n=5.解得n=1,m=
m+n=1+=,故答案为:.
14. .
【解答】解:由已知等式,得(x﹣2y)2+(x+3)2=0,
根据非负数的性质,得x﹣2y=0,x+3=0,解得x=﹣3,y=﹣,
∴x+y=﹣3﹣=﹣.故答案为:﹣.
15. (x﹣)(x+)(x2+3) .
【解答】解:x4﹣9=(x2)2﹣32=(x2﹣3)(x2+3)=(x﹣)(x+)(x2+3).
故答案为:(x﹣)(x+)(x2+3).
16. (x2+x+5)(x+2)(x﹣1) .
【解答】解:原式=(x2+x)2+3(x2+x)﹣10=(x2+x+5)(x2+x﹣2)=(x2+x+5)(x+2)(x﹣1).
故答案为:(x2+x+5)(x+2)(x﹣1).
17. ±4xy、 .
【解答】解:∵x2y2+4±4xy=(xy±2)2;
x2y2+4+=(+2)2;∴加上的单项式可以是±4xy、中任意一个.
故答案为:±4xy、.
18. 21 .
【解答】解:由图中的规律可知:上面两个数之和就是下面的一行的数;
∴第7行的数是:1 7 21 35 35 21 7 1
故(a+b)7展开后从左向右第三项的系数是21故答案为:21
三.解答题(共9小题)
19.【解答】解:(1)原式=4x2+9y2+12xy﹣16x2+81y2+9x2+4y2﹣12xy=﹣3x2+94y2;
(2)原式=a2﹣4ab+4b2﹣b2+4a2﹣4a2+4ab=a2+3b2.
20.【解答】解:(1)原式=(x2+9)(x2﹣9)=(x2+9)(x+3)(x﹣3);
(2)原式=3x(x2﹣4y2)=3x(x+2y)(x﹣2y);
(3)原式=(2x+2y+1)(2x+2y﹣1);
(4)原式=(x2+x+1+1)(x2+x+1﹣1)=(x2+x+2)(x2+x);
(5)原式=[3(x+y)+2(x﹣y)][3(x+y)﹣2(x﹣y)]=(5x+y)(x+5y).
21.【解答】解:分三种情况:
①(x2+x﹣1)+(x2+3x+1)=x2+x﹣1+x2+3x+1=x2+4x=x(x+4);
②(x2+x﹣1)+(x2﹣x)=x2+x﹣1+x2﹣x=x2﹣1=(x+1)(x﹣1);
③(x2+3x+1)+(x2﹣x)=x2+3x+1+x2﹣x=x2+2x+1=(x+1)2.
22.【解答】解:(1)原式=x2﹣y2﹣x2﹣xy+2xy=﹣y2+xy
将x=1,y=2代入得:原式=﹣2;
(2)原式=a2+2ab+b2﹣2ab﹣2a﹣a2=b2﹣2a,
将a=﹣2,b=2代入得:原式=8.
23.【解答】解:(1)方程左边因式分解可得:x(2x﹣1)=0,∴x=0或2x﹣1=0,
解得:x=0或x=;
(2)原方程整理可得:x2+3x+=0,
左边因式分解可得:(x+)2=0,∴x+=0,解得:x=﹣.
24.【解答】解:根据题意得a2+b2=52=25,a 2b=24,∴a2+b2+2ab49,
∴a+b=7,∵a>b,∴a=4,b=3,∴a2+b2=25,a2﹣b2=7.
25.【解答】解:△ABC为直角三角形
理由:∵a2+b2+c2﹣12a﹣16b﹣20c+200
=a2﹣12a+36+b2﹣16b+64+c2﹣20c+100
=(a﹣6)2+(b﹣8)2+(c﹣10)2=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,∴a=6,b=8,c=10,
∴a2+b2=36+64=100=c2∴△ABC为直角三角形.
26.【解答】解:(1)∵28=82﹣62,2012=5042﹣5022,
∴28是“神秘数”;2012是“神秘数”;
(2)两个连续偶数构成的“神秘数”是4的倍数.理由如下:
(2k+2)2﹣(2k)2=(2k+2+2k)(2k+2﹣2k)=2(4k+2)=4(2k+1),
∴两个连续偶数构成的“神秘数”是4的倍数,
∵2k+1是奇数,∴它是4的倍数,不是8的倍数;
(3)设两个连续的奇数为:2k+1,2k﹣1,则
(2k+1)2﹣(2k﹣1)2=8k,
此数是8的倍数,而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
27.【解答】解:(1)阴影部分为边长为(b﹣a)的正方形,所以阴影部分的面积(b﹣a)2,
故答案为:(b﹣a)2;
(2)图2中,用边长为a+b的正方形的面积减去边长为b﹣a的正方形等于4个长宽分别a、b的矩形面积,所以(a+b)2﹣(a﹣b)2=4ab,21教育网
故答案为:(a+b)2﹣(a﹣b)2=4ab;
(3)∵(x+y)2﹣(x﹣y)2=4xy,而x+y=7,x y=,
∴72﹣(x﹣y)2=4×,∴(x﹣y)2=4,∴x﹣y=±2,
故答案为:±2;
(4)边长为(a+b)与(3a+b)的矩形面积为(a+b)(3a+b),它由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成,www.21-cn-jy.com
∴3a2+4ab+b2=(a+b) (3a+b),
故答案为:3a2+4ab+b2=(a+b) (3a+b).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
