人教版高中物理必修二第六章第4节万有引力理论的成就课件1(33张PPT)
文档属性
| 名称 | 人教版高中物理必修二第六章第4节万有引力理论的成就课件1(33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-11-27 09:31:49 | ||
图片预览








文档简介
课件33张PPT。6.4 万有引力理论的成就万有引力定律的发现对天文学的发展起到了巨大的推动作用,尤其在天体物理学计算、天文观测、卫星发射和回收等天文活动中,万有引力定律可称为最有力的工具。 新课导入卫星在飞行的过程中,地面工作人员根据卫星离地面的高度,就可以判断卫星的飞行速度。你知道他们是怎么计算出的吗?1.了解万有引力定律在天文学上的应用。 2.会用万有引力定律计算天体的质量和密度。3.掌握综合运用万有引力定律和圆周运动学知识分析具体问题的方法。学习目标阿基米德在研究杠杆原理后,曾经说过一句什么名言? “给我一个支点,我可以撬动地球。” 那我们又是怎么知道巨大的地球的质量的呢?那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?不能课堂探究一百多年前,英国人卡文迪许用他自己设计的扭秤,“第一次称出了地球的质量”。 一、科学真是迷人称量地球的重量 1.卡文迪许为什么说自己的实验是“称量地球的重量(质量)”?请你解释一下原因。 不考虑地球自转的影响 M是地球质量,r是物体距地心的距离,
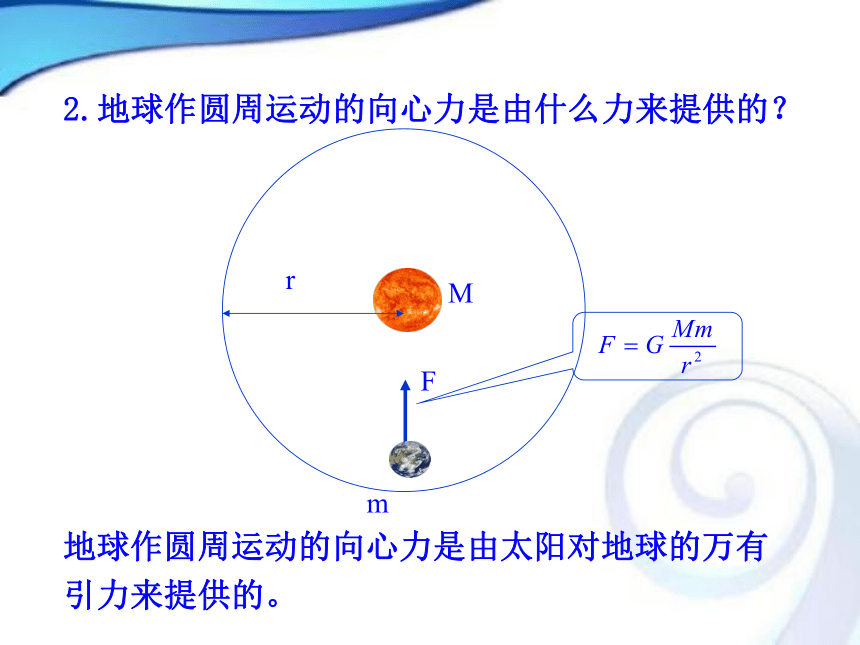
即地球半径R 重力加速度g和地球半径R在卡文迪许之前就知道了,一旦测得引力常量G,则可以计算出地球的质量M。 例1.设地面附近的重力加速度g=9.8m/s2,地球半径R=6.4×106m,引力常量G=6.67×10-11N·m2/kg2,试估算地球的质量。 答案:6×1024kg解: 1.地球实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?用万有引力定律可算出地球的质量,能否用它算出太阳的质量呢?通常可以认为地球绕太阳做匀速圆周运动。二、计算天体的质量 2.地球作圆周运动的向心力是由什么力来提供的?rMmF地球作圆周运动的向心力是由太阳对地球的万有
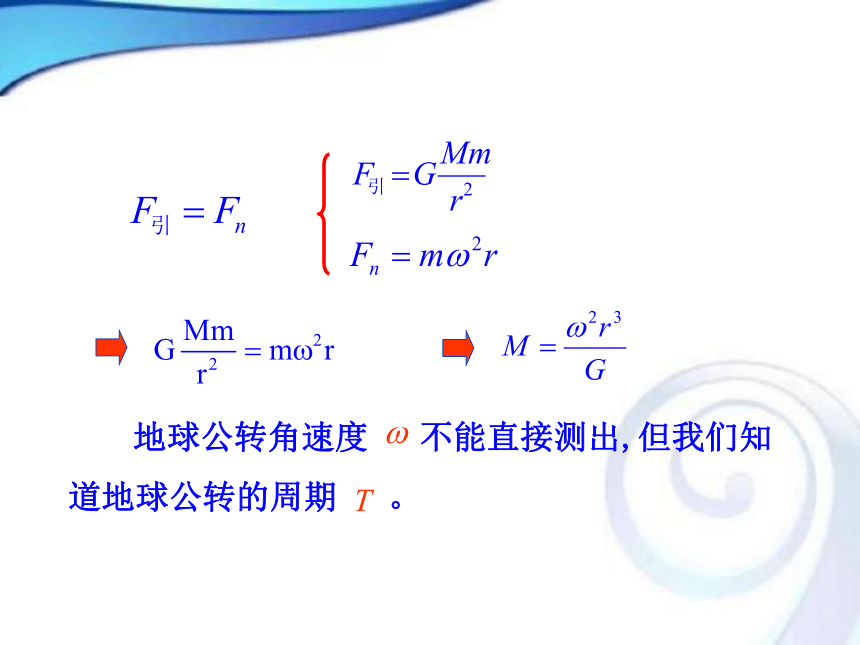
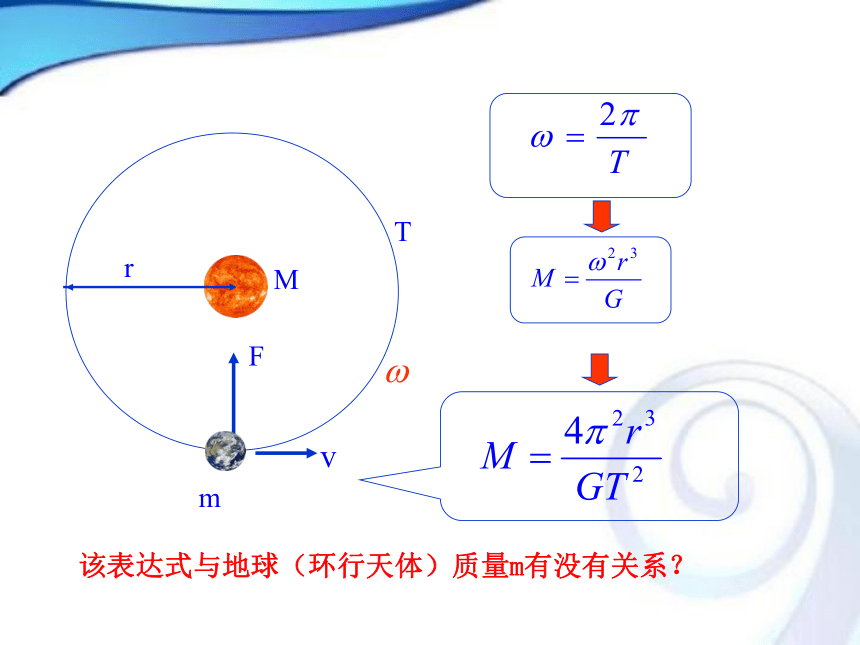
引力来提供的。 地球公转角速度 不能直接测出,但我们知道地球公转的周期 。该表达式与地球(环行天体)质量m有没有关系?rM mFT例2.把地球绕太阳的公转看作是匀速圆周运动,轨道半径约为1.5×1011 m,已知引力常量G=6.67×10-11 N·m2/kg2,则可估算出太阳的质量约为 kg。解:地球绕太阳运转的周期:
T=365×24×60×60s=3.15×107s
地球绕太阳做匀速圆周运动的向心力由万有引力提供,答案:2×1030
【提示】解题时经常需要引用一些常数,如地球自转周期、月球公转周期等。应注意挖掘使用。1.物体在天体表面时受到的重力等于万有引力g--天体表面的重力加速度R--天体的半径【方法总结】计算天体质量的两条基本思路2.行星(或卫星)做匀速圆周运动所需的万有引力
提供向心力只能求出中心天体的质量!!!
根据上面两种方式算出中心天体的质量M,
结合球体体积计算公式
物体的密度计算公式
求出中心天体的密度当r=R时例3.宇航员站在一个星球表面上的某高处h自由释放一小球,经过时间t落地,该星球的半径为R,你能求解出该星球的质量吗? 解析:由星球表面附近重力等于万有引力得解得:释放小球后小球做匀加速运动故星球质量为例4.一艘宇宙飞船飞近某一个不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进行预定的考察工作,宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程。解析:r=R特别提醒
利用万有引力定律提供向心力,我们只能求出中心天体的质量和密度。所以要求太阳的质量和密度就要以它的行星为研究对象。若要求地球的质量和密度,就要以它的卫星为研究对象;也可以以地面上的物体利用重力近似等于万有引力求得。海王星的轨道由英国剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶各自独立计算出来。1846年9月23日晚,由德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。海王星三、预测未知天体—海王星的发现 当时有两个青年——英国的
亚当斯和法国的勒维耶在互不
知晓的情况下分别进行了整整
两年的工作。1845年亚当斯先
算出结果,但格林尼治天文台
却把他的论文束之高阁。1846年
9月18日,勒维耶把结果寄到了柏林,却受到了重视。柏林天文台的伽勒于1846年9月23日晚就进行了搜索,并且在离勒维耶预报位置不远的地方发现了这颗新行星。 海王星的发现使哥白尼学说和牛顿力学得到了最好的证明。科学史上的一段佳话 海王星发现之后,人们发现它的轨道也与理论计算的
不一致。于是几位学者用亚当斯和勒维耶列的方法预言另
一颗行星的存在。
在预言提出之后,1930年3月14日,汤博发现了这颗行
星——冥王星。两条基本思路1.重力等于万有引力2.万有引力提供向心力课堂小结1.飞船在某行星表面附近沿圆轨道绕该行星飞
行,认为行星是密度均匀的球体,要确定该行星
的密度,只需要测量( )
A.飞船的轨道半径
B.飞船的质量
C.飞船的运行周期
D.行星的质量AC课堂训练2.设行星绕恒星的运动轨道是圆,则其运行周期T的
平方与其运动轨道半径R的三次方之比为常量k,那么
k的大小( )
A.只与行星质量有关
B.只与恒星质量有关
C.与行星及恒星的速度都有关
D.以上都不正确B3.若已知太阳的一个行星绕太阳运转的轨道半径为r,
周期为T,引力常数为G,则可求得( )
A.该行星的质量
B.太阳的质量
C.该行星的平均密度
D.太阳的平均密度B4.中子星是恒星演化过程的一种可能结果,它的密
度很大。现有一中子星,观测到它的自转周期为T=
s。问该中子星的最小密度应是多少才能维持该
星的稳定,不致因自转而瓦解。计算时星体可视为
均匀球体。(引力常量 )解析:设想中子星赤道处有一小物块,只有当它受到的万有引力大于或等于它随星体运动所需的向心力时,中子星才不会瓦解。设中子星的密度为ρ,质量为M ,半径为R,其周期为T,位于赤道处的小物块质量为m,则有
由以上各式得
代入数据解得: 5.(2014·新课标全国卷Ⅱ)假设地球可视为质量均
匀分布的球体。已知地球表面重力加速度在两极的
大小为g0;在赤道的大小为g;地球自转的周期为T,
引力常量为G。地球的密度为( )
A. B.
C. D. B
即地球半径R 重力加速度g和地球半径R在卡文迪许之前就知道了,一旦测得引力常量G,则可以计算出地球的质量M。 例1.设地面附近的重力加速度g=9.8m/s2,地球半径R=6.4×106m,引力常量G=6.67×10-11N·m2/kg2,试估算地球的质量。 答案:6×1024kg解: 1.地球实际轨道是什么形状?为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?用万有引力定律可算出地球的质量,能否用它算出太阳的质量呢?通常可以认为地球绕太阳做匀速圆周运动。二、计算天体的质量 2.地球作圆周运动的向心力是由什么力来提供的?rMmF地球作圆周运动的向心力是由太阳对地球的万有
引力来提供的。 地球公转角速度 不能直接测出,但我们知道地球公转的周期 。该表达式与地球(环行天体)质量m有没有关系?rM mFT例2.把地球绕太阳的公转看作是匀速圆周运动,轨道半径约为1.5×1011 m,已知引力常量G=6.67×10-11 N·m2/kg2,则可估算出太阳的质量约为 kg。解:地球绕太阳运转的周期:
T=365×24×60×60s=3.15×107s
地球绕太阳做匀速圆周运动的向心力由万有引力提供,答案:2×1030
【提示】解题时经常需要引用一些常数,如地球自转周期、月球公转周期等。应注意挖掘使用。1.物体在天体表面时受到的重力等于万有引力g--天体表面的重力加速度R--天体的半径【方法总结】计算天体质量的两条基本思路2.行星(或卫星)做匀速圆周运动所需的万有引力
提供向心力只能求出中心天体的质量!!!
根据上面两种方式算出中心天体的质量M,
结合球体体积计算公式
物体的密度计算公式
求出中心天体的密度当r=R时例3.宇航员站在一个星球表面上的某高处h自由释放一小球,经过时间t落地,该星球的半径为R,你能求解出该星球的质量吗? 解析:由星球表面附近重力等于万有引力得解得:释放小球后小球做匀加速运动故星球质量为例4.一艘宇宙飞船飞近某一个不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进行预定的考察工作,宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程。解析:r=R特别提醒
利用万有引力定律提供向心力,我们只能求出中心天体的质量和密度。所以要求太阳的质量和密度就要以它的行星为研究对象。若要求地球的质量和密度,就要以它的卫星为研究对象;也可以以地面上的物体利用重力近似等于万有引力求得。海王星的轨道由英国剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶各自独立计算出来。1846年9月23日晚,由德国的伽勒在勒维耶预言的位置附近发现了这颗行星,人们称其为“笔尖下发现的行星”。海王星三、预测未知天体—海王星的发现 当时有两个青年——英国的
亚当斯和法国的勒维耶在互不
知晓的情况下分别进行了整整
两年的工作。1845年亚当斯先
算出结果,但格林尼治天文台
却把他的论文束之高阁。1846年
9月18日,勒维耶把结果寄到了柏林,却受到了重视。柏林天文台的伽勒于1846年9月23日晚就进行了搜索,并且在离勒维耶预报位置不远的地方发现了这颗新行星。 海王星的发现使哥白尼学说和牛顿力学得到了最好的证明。科学史上的一段佳话 海王星发现之后,人们发现它的轨道也与理论计算的
不一致。于是几位学者用亚当斯和勒维耶列的方法预言另
一颗行星的存在。
在预言提出之后,1930年3月14日,汤博发现了这颗行
星——冥王星。两条基本思路1.重力等于万有引力2.万有引力提供向心力课堂小结1.飞船在某行星表面附近沿圆轨道绕该行星飞
行,认为行星是密度均匀的球体,要确定该行星
的密度,只需要测量( )
A.飞船的轨道半径
B.飞船的质量
C.飞船的运行周期
D.行星的质量AC课堂训练2.设行星绕恒星的运动轨道是圆,则其运行周期T的
平方与其运动轨道半径R的三次方之比为常量k,那么
k的大小( )
A.只与行星质量有关
B.只与恒星质量有关
C.与行星及恒星的速度都有关
D.以上都不正确B3.若已知太阳的一个行星绕太阳运转的轨道半径为r,
周期为T,引力常数为G,则可求得( )
A.该行星的质量
B.太阳的质量
C.该行星的平均密度
D.太阳的平均密度B4.中子星是恒星演化过程的一种可能结果,它的密
度很大。现有一中子星,观测到它的自转周期为T=
s。问该中子星的最小密度应是多少才能维持该
星的稳定,不致因自转而瓦解。计算时星体可视为
均匀球体。(引力常量 )解析:设想中子星赤道处有一小物块,只有当它受到的万有引力大于或等于它随星体运动所需的向心力时,中子星才不会瓦解。设中子星的密度为ρ,质量为M ,半径为R,其周期为T,位于赤道处的小物块质量为m,则有
由以上各式得
代入数据解得: 5.(2014·新课标全国卷Ⅱ)假设地球可视为质量均
匀分布的球体。已知地球表面重力加速度在两极的
大小为g0;在赤道的大小为g;地球自转的周期为T,
引力常量为G。地球的密度为( )
A. B.
C. D. B
