1.4.1有理数的乘法 第一课时(课件)
文档属性
| 名称 | 1.4.1有理数的乘法 第一课时(课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-28 16:15:50 | ||
图片预览







文档简介
(共23张PPT)
有理数的乘法(第一课时)
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
由于长期干旱,水库放水抗旱.每天放水2米,已经放了3天,现在水深20米,问放水抗旱前水库水深多少米?
20+2×3=26(米).
教学目标
新课讲解
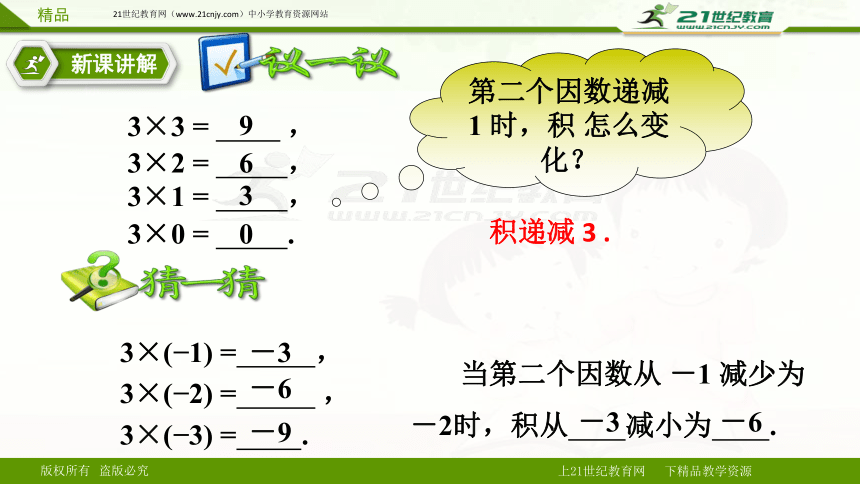
3×3 = ,
3×2 = ,
3×1 = ,
3×0 = .
9
6
3
0
3×( 1) = ,
3×( 2) = ,
3×( 3) = .
第二个因数递减 1 时,积 怎么变化?
-3
-6
-9
当第二个因数从 -1 减少为 -2时,积从 减小为 .
积递减 3 .
-3
-6
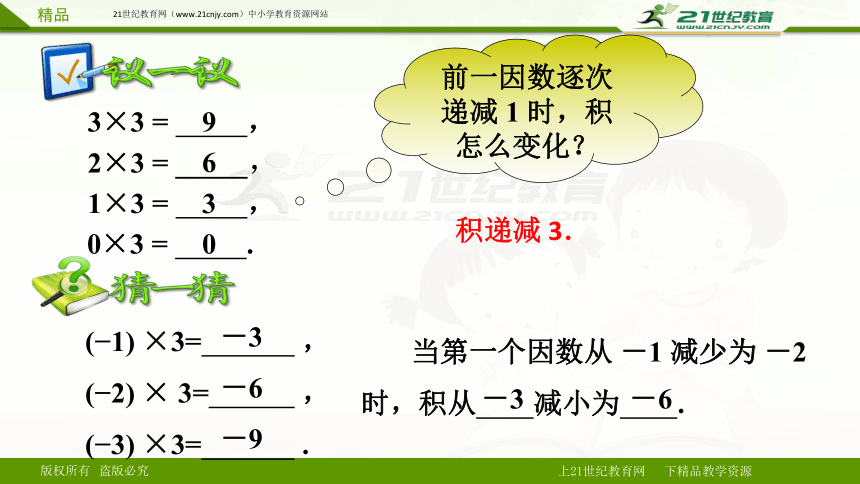
3×3 = ,
2×3 = _____,
1×3 = ,
0×3 = .
9
6
3
0
( 1) ×3= ,
( 2) × 3= ,
( 3) ×3= .
前一因数逐次递减 1 时,积 怎么变化?
-3
-6
-9
当第一个因数从 -1 减少为 -2时,积从 减小为 .
积递减 3.
-3
-6
( 3)×3 = ,
( 3)×2 = ,
( 3)×1 = ,
( 3)×0 = .
9
6
3
0
( 3)×( 1) = ,
( 3)×( 2) = ,
( 3)×( 3) = .
第二个因数减少 1 时,积 怎么变化?
3
6
9
当第二个因数从 -1 减少为 -2时,积从 增大为 .
积增大 3
3
6
( 3)×4 = ,
( 3)×3 = ,
( 3)×2 = ,
( 3)×1 = ,
( 3)×0 = ,
9
6
3
0
由上述所列各式 , 你能看出两有理数相乘与它们的积之间的规律吗?
负数乘正数得负,绝对值相乘;
负数乘 0 得 0 ;
12
由上述所列各式 , 你能看出两有理数相乘与它们的积之间的规律吗?
( 3)×( 1) = ,
( 3)×( 2) = ,
( 3)×( 3) = ,
( 3)×( 4) = .
3
6
9
12
负数乘负数得正,绝对值相乘.
试用简练的语言叙述上面得出的结论.
两数相乘,同号得 ,异号得 ,并把绝对值相乘;任何数同0相乘,都得0.
正
负
想一想怎样利用法则来进行两有理数的乘法运算?
乘积的符号的确定:
试一试身手:口答下列算式的结果.
(-3)×(+3), 5×(-2),
(-8)×8, (-5)×(-4), (-9)×0.
分析:进行有理数乘法,先要判断两个因数是同号还是异号,有一个因数是否为零;也就是先判断积的符号,然后再把绝对值相乘.
答案:-9;-10;-64;20;0.
解:(1)(-3)×9=
-27;
(2)8×(-1)=-8;
例1:计算:(1) (-3)×9;(2) 8×(-1);
(异号相乘得负,再把绝对值相乘)
(3) .
(异号相乘得负,再把绝对值相乘)
数a(a≠0)的
倒数是什么?
乘积是1的两个数互为倒数.
(同号相乘得正)
解:(3) =1.
有理数相乘,先确定积的符号,再确定积的绝对值.
例1:计算:(1) (-3)×9;(2) 8×(-1);
(3) .
例2 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1 km气温的变化量为-6 ℃,攀登3 km后,气温有什么变化?
解:(-6)×3=-18.
答:气温下降18 ℃.
下列各式的积是正的还是负的?
2×3×4×(-5)=
2×3×(-4)×(-5)=
2×(-3)×(-4)×(-5)=
(-2)×(-3)×(-4)×(-5)=
-120;
120;
-120;
120.
只考虑积的符号,第一、三式的积是负的,第二、四式的积是正的.
几个有理数相乘,因数都不为 0 时,积的符号怎样确定?
有一因数为 0 时,积是多少?
几个有理数相乘,因数都不为 0 时,积的符号由负因数的个数确定:
奇数个为负,偶数个为正.
你能看出下式的结果吗?如果能,请说明理由.
7.8×(-8.1)×0×(-19.6)
几个数相乘,如果其中有因数为0,积等于0.
例3 计算:
解:(1)
(1)
;
(2)
.
解:(2)
先确定积的符号,再把各个乘数的绝对值相乘,作为积的绝对值.
例3 计算:
(1)
;
(2)
.
巩固练习
解:(1)原式=-(125×2×8)=-2 000.
计算:
(1)(-125)×(-2)×(-8).
(2)
(2)原式=
计算:
(3)22×(-33)×(-4)×0.
解:(3)原式=0.
=-18.
(4)
(4)原式=
课堂小结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和0相乘,都得0.
2.有理数相乘,可以先确定积的符号,再确定积的绝对值.
3.几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
有理数的乘法(第一课时)
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
由于长期干旱,水库放水抗旱.每天放水2米,已经放了3天,现在水深20米,问放水抗旱前水库水深多少米?
20+2×3=26(米).
教学目标
新课讲解
3×3 = ,
3×2 = ,
3×1 = ,
3×0 = .
9
6
3
0
3×( 1) = ,
3×( 2) = ,
3×( 3) = .
第二个因数递减 1 时,积 怎么变化?
-3
-6
-9
当第二个因数从 -1 减少为 -2时,积从 减小为 .
积递减 3 .
-3
-6
3×3 = ,
2×3 = _____,
1×3 = ,
0×3 = .
9
6
3
0
( 1) ×3= ,
( 2) × 3= ,
( 3) ×3= .
前一因数逐次递减 1 时,积 怎么变化?
-3
-6
-9
当第一个因数从 -1 减少为 -2时,积从 减小为 .
积递减 3.
-3
-6
( 3)×3 = ,
( 3)×2 = ,
( 3)×1 = ,
( 3)×0 = .
9
6
3
0
( 3)×( 1) = ,
( 3)×( 2) = ,
( 3)×( 3) = .
第二个因数减少 1 时,积 怎么变化?
3
6
9
当第二个因数从 -1 减少为 -2时,积从 增大为 .
积增大 3
3
6
( 3)×4 = ,
( 3)×3 = ,
( 3)×2 = ,
( 3)×1 = ,
( 3)×0 = ,
9
6
3
0
由上述所列各式 , 你能看出两有理数相乘与它们的积之间的规律吗?
负数乘正数得负,绝对值相乘;
负数乘 0 得 0 ;
12
由上述所列各式 , 你能看出两有理数相乘与它们的积之间的规律吗?
( 3)×( 1) = ,
( 3)×( 2) = ,
( 3)×( 3) = ,
( 3)×( 4) = .
3
6
9
12
负数乘负数得正,绝对值相乘.
试用简练的语言叙述上面得出的结论.
两数相乘,同号得 ,异号得 ,并把绝对值相乘;任何数同0相乘,都得0.
正
负
想一想怎样利用法则来进行两有理数的乘法运算?
乘积的符号的确定:
试一试身手:口答下列算式的结果.
(-3)×(+3), 5×(-2),
(-8)×8, (-5)×(-4), (-9)×0.
分析:进行有理数乘法,先要判断两个因数是同号还是异号,有一个因数是否为零;也就是先判断积的符号,然后再把绝对值相乘.
答案:-9;-10;-64;20;0.
解:(1)(-3)×9=
-27;
(2)8×(-1)=-8;
例1:计算:(1) (-3)×9;(2) 8×(-1);
(异号相乘得负,再把绝对值相乘)
(3) .
(异号相乘得负,再把绝对值相乘)
数a(a≠0)的
倒数是什么?
乘积是1的两个数互为倒数.
(同号相乘得正)
解:(3) =1.
有理数相乘,先确定积的符号,再确定积的绝对值.
例1:计算:(1) (-3)×9;(2) 8×(-1);
(3) .
例2 用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1 km气温的变化量为-6 ℃,攀登3 km后,气温有什么变化?
解:(-6)×3=-18.
答:气温下降18 ℃.
下列各式的积是正的还是负的?
2×3×4×(-5)=
2×3×(-4)×(-5)=
2×(-3)×(-4)×(-5)=
(-2)×(-3)×(-4)×(-5)=
-120;
120;
-120;
120.
只考虑积的符号,第一、三式的积是负的,第二、四式的积是正的.
几个有理数相乘,因数都不为 0 时,积的符号怎样确定?
有一因数为 0 时,积是多少?
几个有理数相乘,因数都不为 0 时,积的符号由负因数的个数确定:
奇数个为负,偶数个为正.
你能看出下式的结果吗?如果能,请说明理由.
7.8×(-8.1)×0×(-19.6)
几个数相乘,如果其中有因数为0,积等于0.
例3 计算:
解:(1)
(1)
;
(2)
.
解:(2)
先确定积的符号,再把各个乘数的绝对值相乘,作为积的绝对值.
例3 计算:
(1)
;
(2)
.
巩固练习
解:(1)原式=-(125×2×8)=-2 000.
计算:
(1)(-125)×(-2)×(-8).
(2)
(2)原式=
计算:
(3)22×(-33)×(-4)×0.
解:(3)原式=0.
=-18.
(4)
(4)原式=
课堂小结
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数和0相乘,都得0.
2.有理数相乘,可以先确定积的符号,再确定积的绝对值.
3.几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
