3.2解一元一次方程(一)第一课时 ——合并同类项(课件)
文档属性
| 名称 | 3.2解一元一次方程(一)第一课时 ——合并同类项(课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-28 11:28:03 | ||
图片预览








文档简介
(共21张PPT)
解一元一次方程(一)-合并同类项
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
在多项式中,所含字母相同,并且相同的字母的次数也相同的项叫做同类项.
合并同类项的法则是;同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
1.什么是同类项?怎样合并同类项?
导入新课
2. 你能利用等式的性解方程7x=140 吗?
解: 7x÷7=140÷7 (等式的性质2)
x=20. (x的系数为1)
教学目标
新课讲解
问题 某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了多少台计算机?
解法一:
设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台,
2x
4x
教学目标
新课讲解
根据问题中的相等关系:
前年购买量+去年购买量+今年购买量=140台.
根据题意,列得方程
x+2x+4x=140.
教学目标
新课讲解
还有不同的设法吗?
还可以列怎样的方程?
设去年购买计算机x台.
设今年购买计算机x台.
解法二:
解法三:
问题 某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了多少台计算机?
教学目标
新课讲解
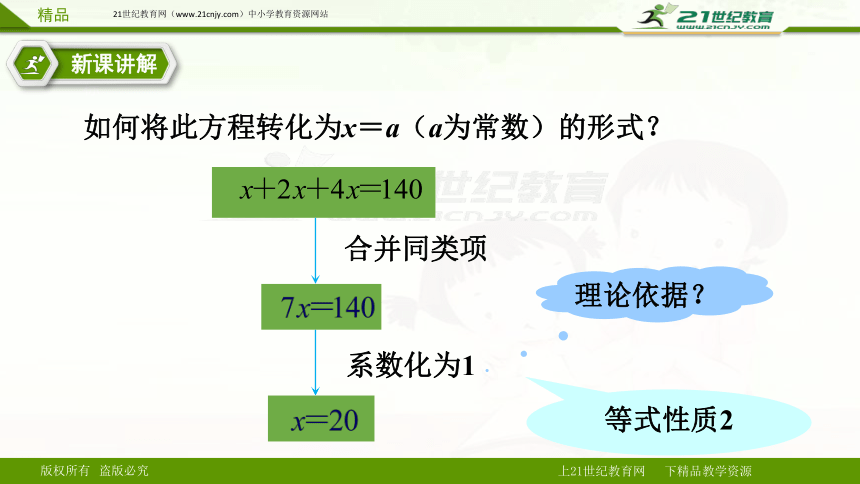
如何将此方程转化为x=a(a为常数)的形式?
合并同类项
系数化为1
等式性质2
理论依据?
教学目标
新课讲解
例1 解下列方程:
解:(1)合并同类项,得
系数化为1,得
(1)
(2)
教学目标
新课讲解
合并同类项,得
系数化为1,得
解:(2)
例1 解下列方程:
(1)
(2)
教学目标
新课讲解
例2 有一列数,按一定规律排列成1,-3,9,-27,81,-243,···,其中某三个相邻数的和是-1 701,这三个数各是多少?
这列数有什么规律?
如何设未知数?
教学目标
新课讲解
解:设所求三个数分别是x,-3x,9x.
由三个数的和是-1 701,得 x-3x+9x=-1 701.
合并同类项,得 7x=-1 701.
系数化为1,得x=-243.
所以-3x=729.
9x=-2 187.
答:这三个数是-243,729,-2 187.
方法一:
教学目标
新课讲解
解:设这三个相邻数中的中间的一个数为 ,则第
一个数为 ,第三个数为 .
根据这三个数的和是-1 701,得
解得
方法二:
教学目标
新课讲解
解:设这三个相邻数中最后1个数为 ,
则第二个数为 ,
第一个数为_________________.
根据这三个数的和是-1 701,得
解得
方法三:
解:(1)合并同类项,得
系数化为1,得
(2)合并同类项,得
1.解下列方程:
(1)
(2)
(3)
(4)
系数化为1,得
巩固练习
巩固练习
解:(3)合并同类项,得
系数化为1,得
(4)合并同类项,得
系数化为1,得
1.解下列方程:
(1)
(2)
(3)
(4)
巩固练习
2.一个数列,按一定规律排列如下形式:
其中某三个相邻的数的和为 ,
求这三个数各是多少?
…,
巩固练习
解:设三个相邻数中第一个数为x,则第二个数为-4x,第三个数为16x.
解得
所以
答:这三个数分别为:
由题意,得
巩固练习
3.我校开展的数学课外兴趣小组活动,每周四进行一次活动,现知本月连续的三次活动的日子之和为27,你知道是哪三天吗?本月的四次活动的日子之和是多少呢?
解:设三次活动的时间分别为:x-7,x,x+7.
根据题意,得x-7+x+x+7=27.解得x=9.
所以这三天为2,9,16.本月的四次活动的时间为2,9,16,23.四次的和为50.
课堂小结
1.列方程的一般步骤是什么?
2.解方程的步骤及依据分别是什么?
3.谈谈你这节课还有什么收获.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
解一元一次方程(一)-合并同类项
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
在多项式中,所含字母相同,并且相同的字母的次数也相同的项叫做同类项.
合并同类项的法则是;同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
1.什么是同类项?怎样合并同类项?
导入新课
2. 你能利用等式的性解方程7x=140 吗?
解: 7x÷7=140÷7 (等式的性质2)
x=20. (x的系数为1)
教学目标
新课讲解
问题 某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了多少台计算机?
解法一:
设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台,
2x
4x
教学目标
新课讲解
根据问题中的相等关系:
前年购买量+去年购买量+今年购买量=140台.
根据题意,列得方程
x+2x+4x=140.
教学目标
新课讲解
还有不同的设法吗?
还可以列怎样的方程?
设去年购买计算机x台.
设今年购买计算机x台.
解法二:
解法三:
问题 某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买的数量又是去年的2倍.前年这个学校购买了多少台计算机?
教学目标
新课讲解
如何将此方程转化为x=a(a为常数)的形式?
合并同类项
系数化为1
等式性质2
理论依据?
教学目标
新课讲解
例1 解下列方程:
解:(1)合并同类项,得
系数化为1,得
(1)
(2)
教学目标
新课讲解
合并同类项,得
系数化为1,得
解:(2)
例1 解下列方程:
(1)
(2)
教学目标
新课讲解
例2 有一列数,按一定规律排列成1,-3,9,-27,81,-243,···,其中某三个相邻数的和是-1 701,这三个数各是多少?
这列数有什么规律?
如何设未知数?
教学目标
新课讲解
解:设所求三个数分别是x,-3x,9x.
由三个数的和是-1 701,得 x-3x+9x=-1 701.
合并同类项,得 7x=-1 701.
系数化为1,得x=-243.
所以-3x=729.
9x=-2 187.
答:这三个数是-243,729,-2 187.
方法一:
教学目标
新课讲解
解:设这三个相邻数中的中间的一个数为 ,则第
一个数为 ,第三个数为 .
根据这三个数的和是-1 701,得
解得
方法二:
教学目标
新课讲解
解:设这三个相邻数中最后1个数为 ,
则第二个数为 ,
第一个数为_________________.
根据这三个数的和是-1 701,得
解得
方法三:
解:(1)合并同类项,得
系数化为1,得
(2)合并同类项,得
1.解下列方程:
(1)
(2)
(3)
(4)
系数化为1,得
巩固练习
巩固练习
解:(3)合并同类项,得
系数化为1,得
(4)合并同类项,得
系数化为1,得
1.解下列方程:
(1)
(2)
(3)
(4)
巩固练习
2.一个数列,按一定规律排列如下形式:
其中某三个相邻的数的和为 ,
求这三个数各是多少?
…,
巩固练习
解:设三个相邻数中第一个数为x,则第二个数为-4x,第三个数为16x.
解得
所以
答:这三个数分别为:
由题意,得
巩固练习
3.我校开展的数学课外兴趣小组活动,每周四进行一次活动,现知本月连续的三次活动的日子之和为27,你知道是哪三天吗?本月的四次活动的日子之和是多少呢?
解:设三次活动的时间分别为:x-7,x,x+7.
根据题意,得x-7+x+x+7=27.解得x=9.
所以这三天为2,9,16.本月的四次活动的时间为2,9,16,23.四次的和为50.
课堂小结
1.列方程的一般步骤是什么?
2.解方程的步骤及依据分别是什么?
3.谈谈你这节课还有什么收获.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
