3.3.解一元一次方程(二)第一课时 ——去括号(课件)
文档属性
| 名称 | 3.3.解一元一次方程(二)第一课时 ——去括号(课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-28 13:12:55 | ||
图片预览








文档简介
(共24张PPT)
解一元一次方程(二)——去括号
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
1.一元一次方程的解法我们学了哪几步?
2.合并同类项及移项的依据是什么?
3.“移项”要注意什么?
移项,合并同类项,系数化为1.
等式的性质.
移项要注意变号.
导入新课
解方程 9-3x=-5x+5.
解:移项,得 5x-3x=-9+5.
合并同类项,得 2x=-4.
系数化为1,得 x=-2.
教学目标
新课讲解
问题 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
你会用方程解这道题吗?
教学目标
新课讲解
作以下分析:
1.本问题的等量关系是什么?
2.如果设上半年每月平均用电x度,那么怎样表示下半年每月平均用电量、上半年共用电量和下半年共用电量?
3.根据等量关系,列出方程.
4.怎样解这个方程?
教学目标
新课讲解
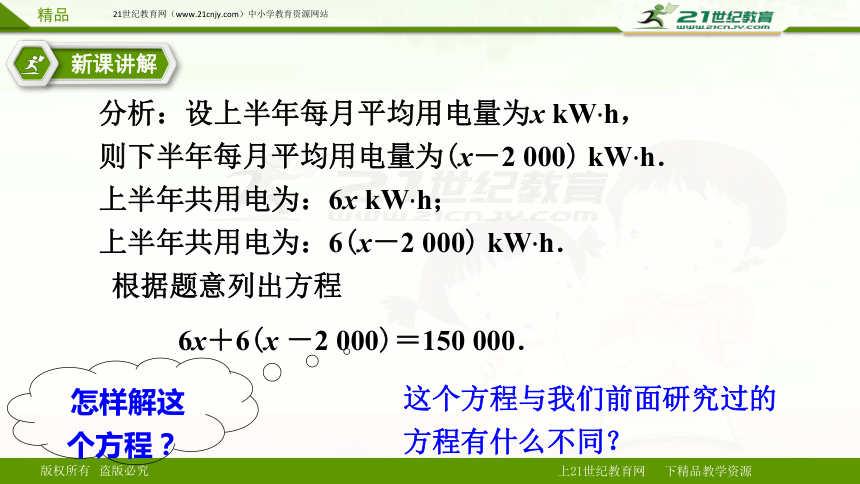
6x+6(x -2 000)=150 000.
分析:设上半年每月平均用电量为x kW·h,
则下半年每月平均用电量为(x-2 000) kW·h.
上半年共用电为:6x kW·h;
上半年共用电为:6(x-2 000) kW·h.
根据题意列出方程
怎样解这个方程?
这个方程与我们前面研究过的方程有什么不同?
教学目标
新课讲解
解:6x+6(x -2 000)=150 000
去括号,得: 6x+6x-12 000=150 000.
思考本题还有其他列方程的方法吗?用其他方法列的方程应怎样解?
答:这个工厂去年上半年每月平均用电13 500度.
移项,得:6x+6x=150 000+12 000.
合并同类项,得:12x=162 000.
系数化为1,得:x=13 500.
教学目标
新课讲解
点拨:如果设去年下半年平均每月用电x度,那么怎样列方程呢?这个方程的解是问题的答案吗?
设去年下半年平均每月用电x度,则上半年平均每月用电(x+2 000)度,
列方程,6(x+2 000)+6x=150 000.
解方程,得x=11 500,
那么上半年平均每月用电量为11 500+2 000=13 500(度).
教学目标
新课讲解
方法一叫直接设元法,方程的解就是问题的答案;方法二是间接设元法,方程的解并不是问题答案,需要根据问题中的数量关系求出最后答案.
方程中有带括号的式子时,利用分配律去括号是常用的化简步骤.
教学目标
新课讲解
系数化为1
去括号
移项
合并同类项
问题 通过以上解方程的过程,你能总结出含有括号的一元一次方程解法的一般步骤吗?
教学目标
新课讲解
分析:按照去括号→移项→合并同类项→系数化为1的步骤解方程.
例1 解下列方程:
(1)2x-(x+10)=5x+2(x-1);
解:去括号,得2x-x-10=5x+2x-2.
移项,得2x-x- 5x-2x =-2+10 .
合并同类项,得-6x =8.
系数化为1,得
教学目标
新课讲解
(2)3x-7(x-1)=3-2(x+3).
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
3x-7x+2x=3-6-7
例1 解下列方程:
3x-7x+7=3-2x-6.
-2x=-10.
x=5.
教学目标
新课讲解
(3)3x-2[3(x-1)-2(x+2)]=3(18-x) .
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
3x-6x+4x+3x = 54-6-8
例1 解下列方程:
3x-6x+6+4x+8=54-3x.
4x=40.
x=10.
教学目标
新课讲解
例2 一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度.
一般情况下可以认为这艘船往返的路程相等,
则顺流速度___顺流时间___逆流速度 ___逆流时间.
×
=
×
教学目标
新课讲解
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据往返路程相等,列出方程,得
去括号,得:
移项及合并同类项,得:
系数化为1,得:
答:船在静水中的平均速度为 27 km/h.
2(x+3)=2.5(x-3).
2x+6=2.5x-7.5.
0.5x=13.5.
x=27.
巩固练习
(1)4x+3(2x-3)=12-(x+4);
解:去括号,得 4x+6x-9=12-x-4.
移项,得4x+6x+x=12+9-4.
合并同类项,得11x=17.
系数化为1,得
解下列方程
巩固练习
(2)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得x=6.
巩固练习
2.甲、乙两人登一座山,甲每分登高10米,并且先出发30分,乙每分登高15米,两人同时登上山顶.甲用多少时间登山?这座山有多高?
解:设甲用x分登山.
由甲先出发30分钟,甲、乙同时到达山顶,则乙用(x-30)分登山;甲每分登高10米,则这座山高表示为10x米,乙每分登高15米,那么这座山高又表示为15(x-30)米,相等关系为10x=15(x-30).
巩固练习
列方程10x=15(x-30).
去括号,得10x=15x-450.
移项,得10x-15x=-450.
合并,得-5x=-450.
系数化为1,得x=90.
把x=90代入10x=900.
答:甲用90分登山,这座山高为900米.
巩固练习
3.一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的航速和两城之间的航程.
解:设无风时飞机的航速为x千米/时,可得顺风飞行的速度为(x+24)千米/时,逆风飞行的速度为(x-24)千米/时,根据顺风飞行路程=逆风飞行路程,列方程:
巩固练习
去括号,得
解方程
移项,合并,得
系数化为1,得
两城之间的航程为
答:无风时飞机的航速为840千米/时,两城间的航程为
2 448千米.
课堂小结
1.谈谈你对形如6x+6(x-2 000)=150 000的方程的解法的认识.
2.说一说你列方程解应用题的思路.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
解一元一次方程(二)——去括号
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
1.一元一次方程的解法我们学了哪几步?
2.合并同类项及移项的依据是什么?
3.“移项”要注意什么?
移项,合并同类项,系数化为1.
等式的性质.
移项要注意变号.
导入新课
解方程 9-3x=-5x+5.
解:移项,得 5x-3x=-9+5.
合并同类项,得 2x=-4.
系数化为1,得 x=-2.
教学目标
新课讲解
问题 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
你会用方程解这道题吗?
教学目标
新课讲解
作以下分析:
1.本问题的等量关系是什么?
2.如果设上半年每月平均用电x度,那么怎样表示下半年每月平均用电量、上半年共用电量和下半年共用电量?
3.根据等量关系,列出方程.
4.怎样解这个方程?
教学目标
新课讲解
6x+6(x -2 000)=150 000.
分析:设上半年每月平均用电量为x kW·h,
则下半年每月平均用电量为(x-2 000) kW·h.
上半年共用电为:6x kW·h;
上半年共用电为:6(x-2 000) kW·h.
根据题意列出方程
怎样解这个方程?
这个方程与我们前面研究过的方程有什么不同?
教学目标
新课讲解
解:6x+6(x -2 000)=150 000
去括号,得: 6x+6x-12 000=150 000.
思考本题还有其他列方程的方法吗?用其他方法列的方程应怎样解?
答:这个工厂去年上半年每月平均用电13 500度.
移项,得:6x+6x=150 000+12 000.
合并同类项,得:12x=162 000.
系数化为1,得:x=13 500.
教学目标
新课讲解
点拨:如果设去年下半年平均每月用电x度,那么怎样列方程呢?这个方程的解是问题的答案吗?
设去年下半年平均每月用电x度,则上半年平均每月用电(x+2 000)度,
列方程,6(x+2 000)+6x=150 000.
解方程,得x=11 500,
那么上半年平均每月用电量为11 500+2 000=13 500(度).
教学目标
新课讲解
方法一叫直接设元法,方程的解就是问题的答案;方法二是间接设元法,方程的解并不是问题答案,需要根据问题中的数量关系求出最后答案.
方程中有带括号的式子时,利用分配律去括号是常用的化简步骤.
教学目标
新课讲解
系数化为1
去括号
移项
合并同类项
问题 通过以上解方程的过程,你能总结出含有括号的一元一次方程解法的一般步骤吗?
教学目标
新课讲解
分析:按照去括号→移项→合并同类项→系数化为1的步骤解方程.
例1 解下列方程:
(1)2x-(x+10)=5x+2(x-1);
解:去括号,得2x-x-10=5x+2x-2.
移项,得2x-x- 5x-2x =-2+10 .
合并同类项,得-6x =8.
系数化为1,得
教学目标
新课讲解
(2)3x-7(x-1)=3-2(x+3).
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
3x-7x+2x=3-6-7
例1 解下列方程:
3x-7x+7=3-2x-6.
-2x=-10.
x=5.
教学目标
新课讲解
(3)3x-2[3(x-1)-2(x+2)]=3(18-x) .
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
3x-6x+4x+3x = 54-6-8
例1 解下列方程:
3x-6x+6+4x+8=54-3x.
4x=40.
x=10.
教学目标
新课讲解
例2 一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度.
一般情况下可以认为这艘船往返的路程相等,
则顺流速度___顺流时间___逆流速度 ___逆流时间.
×
=
×
教学目标
新课讲解
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据往返路程相等,列出方程,得
去括号,得:
移项及合并同类项,得:
系数化为1,得:
答:船在静水中的平均速度为 27 km/h.
2(x+3)=2.5(x-3).
2x+6=2.5x-7.5.
0.5x=13.5.
x=27.
巩固练习
(1)4x+3(2x-3)=12-(x+4);
解:去括号,得 4x+6x-9=12-x-4.
移项,得4x+6x+x=12+9-4.
合并同类项,得11x=17.
系数化为1,得
解下列方程
巩固练习
(2)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得x=6.
巩固练习
2.甲、乙两人登一座山,甲每分登高10米,并且先出发30分,乙每分登高15米,两人同时登上山顶.甲用多少时间登山?这座山有多高?
解:设甲用x分登山.
由甲先出发30分钟,甲、乙同时到达山顶,则乙用(x-30)分登山;甲每分登高10米,则这座山高表示为10x米,乙每分登高15米,那么这座山高又表示为15(x-30)米,相等关系为10x=15(x-30).
巩固练习
列方程10x=15(x-30).
去括号,得10x=15x-450.
移项,得10x-15x=-450.
合并,得-5x=-450.
系数化为1,得x=90.
把x=90代入10x=900.
答:甲用90分登山,这座山高为900米.
巩固练习
3.一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的航速和两城之间的航程.
解:设无风时飞机的航速为x千米/时,可得顺风飞行的速度为(x+24)千米/时,逆风飞行的速度为(x-24)千米/时,根据顺风飞行路程=逆风飞行路程,列方程:
巩固练习
去括号,得
解方程
移项,合并,得
系数化为1,得
两城之间的航程为
答:无风时飞机的航速为840千米/时,两城间的航程为
2 448千米.
课堂小结
1.谈谈你对形如6x+6(x-2 000)=150 000的方程的解法的认识.
2.说一说你列方程解应用题的思路.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
