3.4解决实际问题----电话计费问题(课件)
文档属性
| 名称 | 3.4解决实际问题----电话计费问题(课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-11-28 13:41:06 | ||
图片预览



文档简介
(共17张PPT)
解决实际问题(四)—电话计费问题
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
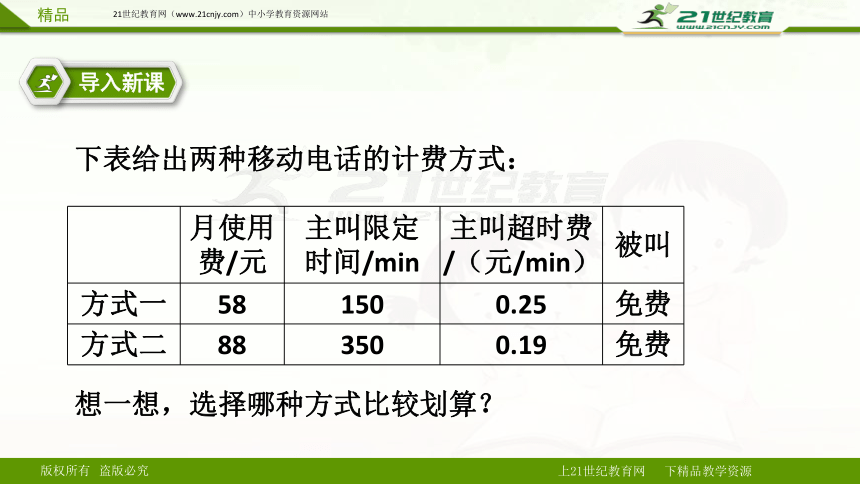
下表给出两种移动电话的计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
想一想,选择哪种方式比较划算?
导入新课
教学目标
新课讲解
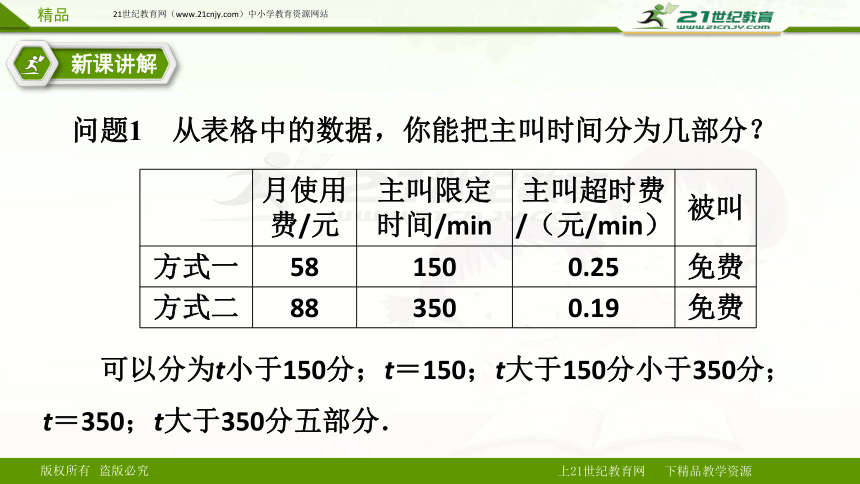
问题1 从表格中的数据,你能把主叫时间分为几部分?
可以分为t小于150分;t=150;t大于150分小于350分;
t=350;t大于350分五部分.
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
教学目标
新课讲解
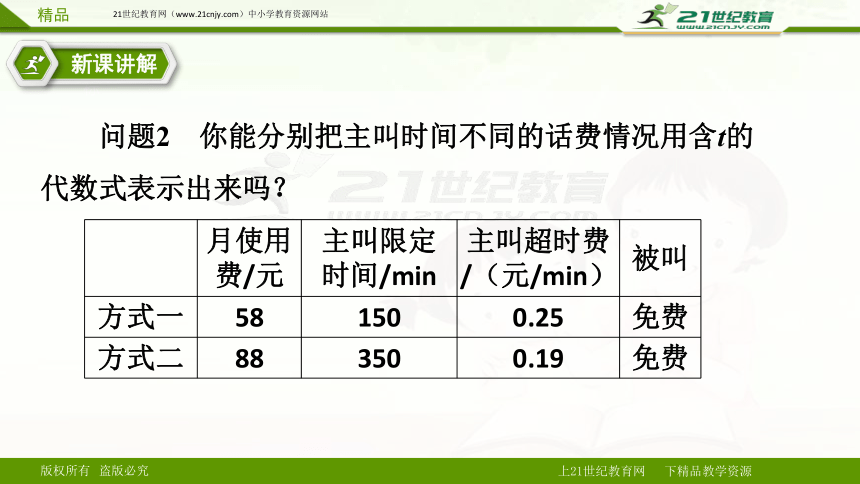
问题2 你能分别把主叫时间不同的话费情况用含t的代数式表示出来吗?
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
教学目标
新课讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t <150 58 88
t =150 58 88
150<t<350 58+0.25(t-150) 88
t =350 108 88
t >350 58+0.25(t-150) 88+0.19(t-350)
教学目标
新课讲解
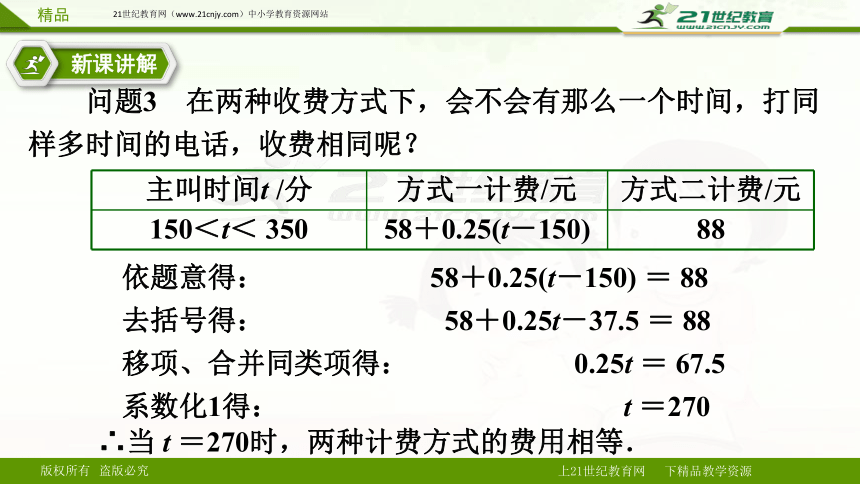
问题3 在两种收费方式下,会不会有那么一个时间,打同样多时间的电话,收费相同呢?
主叫时间t /分 方式一计费/元 方式二计费/元
150<t< 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
∴当 t =270时,两种计费方式的费用相等.
教学目标
新课讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题4 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
教学目标
新课讲解
①从表格中,可以看出当t小于和等150时,按方式一的计费少.
②当 t =270分时,两种计费方式的费用相等,都是88元.
综合以上的分析,可以发现
t 大于150且小于 270分时,选择方式一省钱;
t 大于 270且小于350分时,选择方式二省钱.
教学目标
新课讲解
③当t=350时,按方式二的计费少.
④当t大于350时,可以看出,按方式一的计费为108元加上超出350分的部分的超时费0.25(t-350),按方式二的计费为88元加上超时费0.19(t-350),故按方式二的计费少.
根据以上的分析,可以发现
当t小于270分时选择方案一省钱;当t大于270分时,选择方案二省钱.
利用我们在“电话计费问题”中学会的方法,探究下面的问题.
某市出租车的起步价是7元(起步价是指不超过3 km行程的出租车价格),超过3 km行程后,其中除3 km的行程按起步价计费外,超过部分按每千米1.6元计费(不足1 km按1 km计算).如果仅去程乘出租车而回程不乘坐此车,并且去程超过3 km,那么顾客还需付回程的空驶费,超过3 km部分按每千米0.8元计算空驶费(即超过部分实际按每千米2.4元计费).如果往返都乘坐同一出租车并且中间等候时间不超过3 min,则不收空驶费而加收1.6元等候费.现设小文等4人从市中心A处到相距x km(x小于12)的B处办事,在B处停留时间在3 min内,然后返回A处.现有两种往返方案:
巩固练习
方案一:去时4人乘同一辆出租车,返回都乘公交车(公交车车票为每人2元);
方案二:4人乘同一辆出租车往返.
请问选择哪种方案更省钱?
巩固练习
巩固练习
距离x/km 方案一计费/元 方案二计费/元
x小于等于1.5 7+2×4=15 7+1.6=8.6
x大于1.5且小于等于3 7+2×4=15 7+1.6(2x-3)+1.6
x大于3且小于等于12 7+2.4(x-3)+2×4 7+1.6(2x-3)+1.6
解:对于方案一,路程的关键点是3 km,对于方案二,路程的关键点是1.5 km,故当A处与B处的距离x在不同范围内取值时,对应费用如下表:
巩固练习
(1)当x小于等于1.5时,因为15>8.6,所以选择方案二省钱.
(2)当x大于1.5且小于等于3时,7+1.6(2x-3)+1.6≤7+1.6×(2×3-3)+1.6=13.4<15,所以方案二省钱.
(3)由(2)可知,当x=3时,方案二省钱.当x=12时,方案一的费用是7+2.4×(12-3)+2×4=36.6(元),方案二的费用是7+1.6×(2×12-3)+1.6=42.2(元),所以方案一省钱.
巩固练习
所以在x大于3且小于等于12这一范围内,可能存在使两种方案费用相等的x值.令7+2.4(x-3)+2×4=7+1.6(2x-3)+1.6,解得x=4.所以,当x大于3且小于4时,方案二省钱;当x=4时,两种方案费用相同;当x大于4且小于12时,方案一省钱.
综上分析,当x小于4时,方案二省钱;当x=4时,两种方案费用相同;当x大于4且小于12时,方案一省钱.
课堂小结
谈谈你本节课的收获.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
解决实际问题(四)—电话计费问题
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
下表给出两种移动电话的计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
想一想,选择哪种方式比较划算?
导入新课
教学目标
新课讲解
问题1 从表格中的数据,你能把主叫时间分为几部分?
可以分为t小于150分;t=150;t大于150分小于350分;
t=350;t大于350分五部分.
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
教学目标
新课讲解
问题2 你能分别把主叫时间不同的话费情况用含t的代数式表示出来吗?
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
教学目标
新课讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t <150 58 88
t =150 58 88
150<t<350 58+0.25(t-150) 88
t =350 108 88
t >350 58+0.25(t-150) 88+0.19(t-350)
教学目标
新课讲解
问题3 在两种收费方式下,会不会有那么一个时间,打同样多时间的电话,收费相同呢?
主叫时间t /分 方式一计费/元 方式二计费/元
150<t< 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
∴当 t =270时,两种计费方式的费用相等.
教学目标
新课讲解
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题4 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
教学目标
新课讲解
①从表格中,可以看出当t小于和等150时,按方式一的计费少.
②当 t =270分时,两种计费方式的费用相等,都是88元.
综合以上的分析,可以发现
t 大于150且小于 270分时,选择方式一省钱;
t 大于 270且小于350分时,选择方式二省钱.
教学目标
新课讲解
③当t=350时,按方式二的计费少.
④当t大于350时,可以看出,按方式一的计费为108元加上超出350分的部分的超时费0.25(t-350),按方式二的计费为88元加上超时费0.19(t-350),故按方式二的计费少.
根据以上的分析,可以发现
当t小于270分时选择方案一省钱;当t大于270分时,选择方案二省钱.
利用我们在“电话计费问题”中学会的方法,探究下面的问题.
某市出租车的起步价是7元(起步价是指不超过3 km行程的出租车价格),超过3 km行程后,其中除3 km的行程按起步价计费外,超过部分按每千米1.6元计费(不足1 km按1 km计算).如果仅去程乘出租车而回程不乘坐此车,并且去程超过3 km,那么顾客还需付回程的空驶费,超过3 km部分按每千米0.8元计算空驶费(即超过部分实际按每千米2.4元计费).如果往返都乘坐同一出租车并且中间等候时间不超过3 min,则不收空驶费而加收1.6元等候费.现设小文等4人从市中心A处到相距x km(x小于12)的B处办事,在B处停留时间在3 min内,然后返回A处.现有两种往返方案:
巩固练习
方案一:去时4人乘同一辆出租车,返回都乘公交车(公交车车票为每人2元);
方案二:4人乘同一辆出租车往返.
请问选择哪种方案更省钱?
巩固练习
巩固练习
距离x/km 方案一计费/元 方案二计费/元
x小于等于1.5 7+2×4=15 7+1.6=8.6
x大于1.5且小于等于3 7+2×4=15 7+1.6(2x-3)+1.6
x大于3且小于等于12 7+2.4(x-3)+2×4 7+1.6(2x-3)+1.6
解:对于方案一,路程的关键点是3 km,对于方案二,路程的关键点是1.5 km,故当A处与B处的距离x在不同范围内取值时,对应费用如下表:
巩固练习
(1)当x小于等于1.5时,因为15>8.6,所以选择方案二省钱.
(2)当x大于1.5且小于等于3时,7+1.6(2x-3)+1.6≤7+1.6×(2×3-3)+1.6=13.4<15,所以方案二省钱.
(3)由(2)可知,当x=3时,方案二省钱.当x=12时,方案一的费用是7+2.4×(12-3)+2×4=36.6(元),方案二的费用是7+1.6×(2×12-3)+1.6=42.2(元),所以方案一省钱.
巩固练习
所以在x大于3且小于等于12这一范围内,可能存在使两种方案费用相等的x值.令7+2.4(x-3)+2×4=7+1.6(2x-3)+1.6,解得x=4.所以,当x大于3且小于4时,方案二省钱;当x=4时,两种方案费用相同;当x大于4且小于12时,方案一省钱.
综上分析,当x小于4时,方案二省钱;当x=4时,两种方案费用相同;当x大于4且小于12时,方案一省钱.
课堂小结
谈谈你本节课的收获.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
