4.3.2角的比较与运算(课件)
图片预览





文档简介
(共23张PPT)
角的比较与运算
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
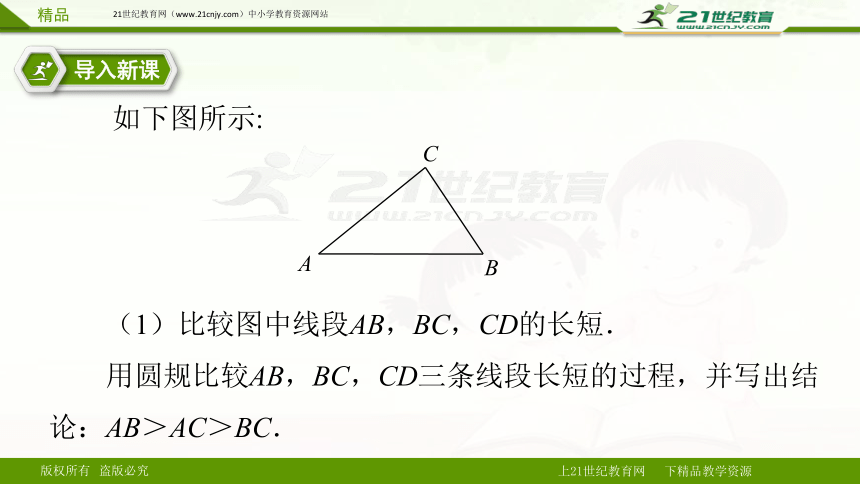
如下图所示:
(1)比较图中线段AB,BC,CD的长短.
用圆规比较AB,BC,CD三条线段长短的过程,并写出结论:AB>AC>BC.
C
B
A
导入新课
(2)怎样比较图中∠A,∠B,∠C的大小?
交流比较方法,得出结论:可用量角器先量出角的度数,然后比较它们的大小.
结论:∠C>∠B>∠A.
类比线段长短的比较方法,也可以把它们叠合在一起比较大小.
教学目标
新课讲解
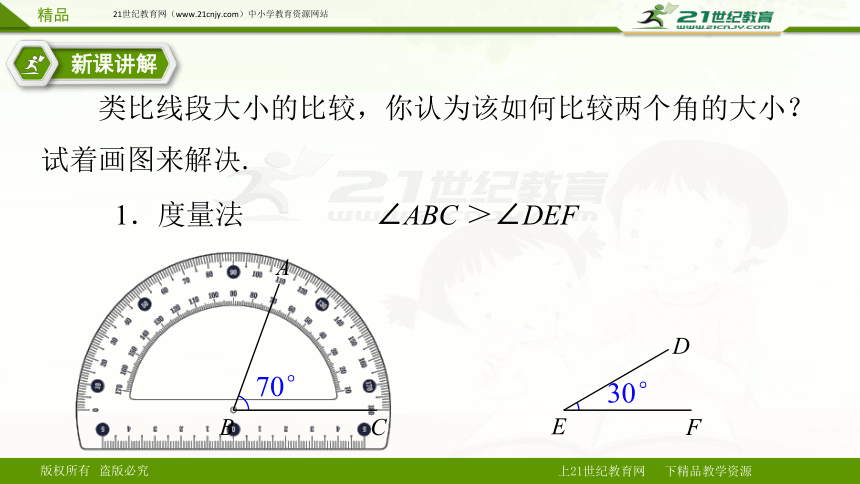
类比线段大小的比较,你认为该如何比较两个角的大小?试着画图来解决.
1.度量法
∠ABC >∠DEF
F
E
D
C
B
A
70°
30°
教学目标
新课讲解
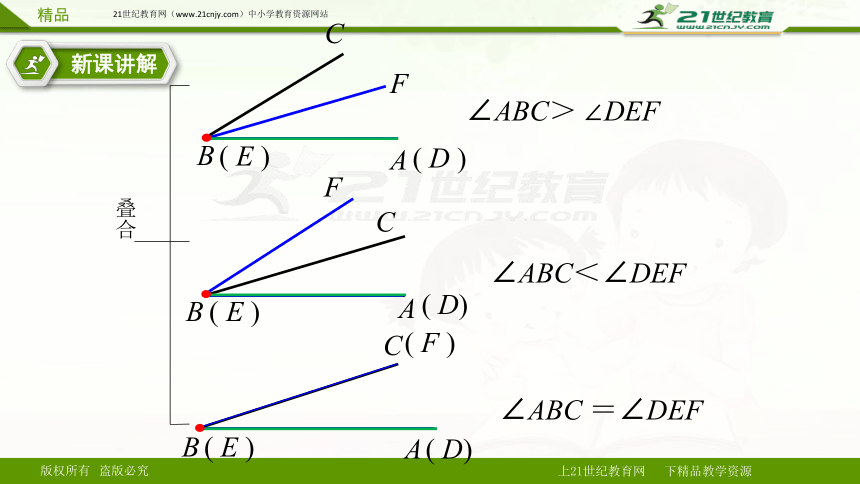
2.叠合法
步骤:
(1) 将两个角的顶点及一边重合,
(2) 两个角的另一边落在重合一边的同侧,
(3)由两个角的另一边的位置确定两个角的大小.
教学目标
新课讲解
A
B
C
F
( E )
( D)
A
B
C
( E )
( D)
( F )
A
B
C
F
( E )
( D )
叠合
∠ABC> ∠DEF
∠ABC<∠DEF
∠ABC =∠DEF
教学目标
新课讲解
3.图中共有几个角?它们之间有什么关系?
有三个角,关系是:
∠BOC=∠AOC-∠AOB.
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
O
C
B
A
教学目标
新课讲解
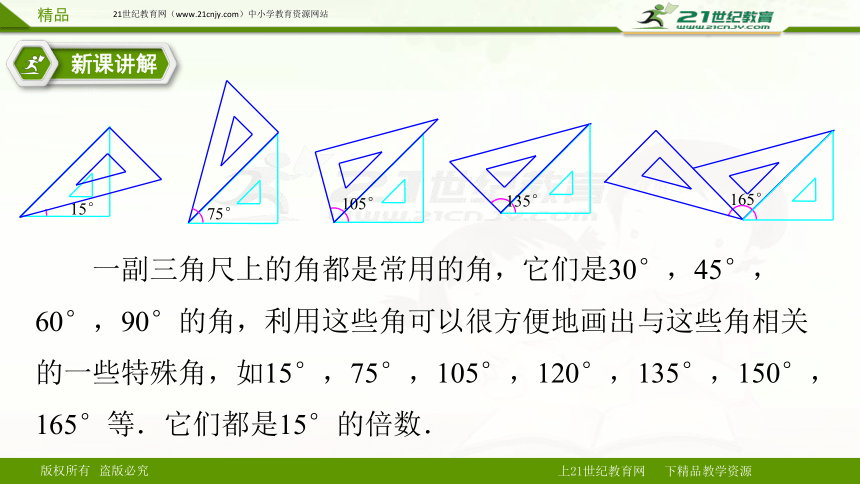
4.利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
15°
75°
教学目标
新课讲解
165°
一副三角尺上的角都是常用的角,它们是30°,45°,60°,90°的角,利用这些角可以很方便地画出与这些角相关的一些特殊角,如15°,75°,105°,120°,135°,150°,165°等.它们都是15°的倍数.
15°
75°
105°
135°
教学目标
新课讲解
在透明纸上画一个角,沿着顶点对折,使角的两边重合.
我们把射线OB叫做∠AOC的角平分线.
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
A
O
C
B
教学目标
新课讲解
角的三等分线.
OB,OC是∠AOD的三等分线.
教学目标
新课讲解
作角平分线有以下两种方法:
(1)借助量角器画图:以已知角顶点为顶点,已知角的一边为边,在已知线的内部画一个度数等于已知角度数一半的角,则这个角的另一边就是已知角的平分线.
(2)用折叠方法:把角沿顶点对折,使角的两边重合,沿折痕在角的内部画一条射线即为已知角的平分线.
教学目标
新课讲解
例1 如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC
=180°- 53 ° 17′
=126°43′.
B
O
C
A
教学目标
新课讲解
例2 把一个周角7等分,每一份是多少度的角(精确到分)?
解:360 ÷7=51 +3 ÷7
=51 +180′÷7
≈51 26′.
答:每份约是51 26′.
巩固练习
1.如图所示,用“=”“>”或“<”填空.
(1)∠AOC ∠AOB+∠BOC;
(2)∠AOC ∠AOB;
(3)∠BOD-∠BOC ∠DOC;
(4)∠AOD ∠AOC+∠BOD.
=
=
>
<
巩固练习
2.如图,将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB和∠DCE的大小关系,并说明理由.
E
D
C
B
A
巩固练习
解:(1)∵∠ECB=90°,∠DCE=35°.
∴∠DCB=90°-35°=55°.
∵∠ACD=90°,
∴∠ACB=∠ACD+∠DCB=145°.
(2)∵∠ACB=140°,∠ACD=90°.
∴∠DCB=140°-90°=50°.
∵∠ECB=90°,
∴∠DCE=90°-50°=40°.
E
D
C
B
A
巩固练习
解:(3)猜想∠ACB+∠DCE=180°.
∵∠ECB=90°,∠ACD=90°.
∴∠ACB=∠ACD+∠DCB=90°+∠DCB.
∵∠DCE=∠ECB-∠DCB=90°-∠DCB.
∴∠ACB+∠DCE=180°.
E
D
C
B
A
巩固练习
3.如图所示,OB,OC是∠AOD的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,则表示∠AOD的代数式是( ).
A.2α-β B.α-β C.α+β D.以上都不正确
N
M
D
C
B
A
O
巩固练习
解析:∵∠MON=α,∠BOC=β,
∴∠MON-∠BOC=∠CON+∠BOM=α-β,
又∵OM平分∠AOB,ON平分∠COD,
∴∠CON=∠DON,∠AOM=∠BOM,
由题意得∠AOD=∠MON+∠DON+∠AOM
=∠MON+∠CON+∠BOM
=α+(α-β)=2α-β.
答案:A.
N
M
D
C
B
A
O
课堂小结
1.谈谈你对角的大小的比较方法的认识.
2.谈谈你对角平分线的认识.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
角的比较与运算
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
如下图所示:
(1)比较图中线段AB,BC,CD的长短.
用圆规比较AB,BC,CD三条线段长短的过程,并写出结论:AB>AC>BC.
C
B
A
导入新课
(2)怎样比较图中∠A,∠B,∠C的大小?
交流比较方法,得出结论:可用量角器先量出角的度数,然后比较它们的大小.
结论:∠C>∠B>∠A.
类比线段长短的比较方法,也可以把它们叠合在一起比较大小.
教学目标
新课讲解
类比线段大小的比较,你认为该如何比较两个角的大小?试着画图来解决.
1.度量法
∠ABC >∠DEF
F
E
D
C
B
A
70°
30°
教学目标
新课讲解
2.叠合法
步骤:
(1) 将两个角的顶点及一边重合,
(2) 两个角的另一边落在重合一边的同侧,
(3)由两个角的另一边的位置确定两个角的大小.
教学目标
新课讲解
A
B
C
F
( E )
( D)
A
B
C
( E )
( D)
( F )
A
B
C
F
( E )
( D )
叠合
∠ABC> ∠DEF
∠ABC<∠DEF
∠ABC =∠DEF
教学目标
新课讲解
3.图中共有几个角?它们之间有什么关系?
有三个角,关系是:
∠BOC=∠AOC-∠AOB.
∠AOC=∠AOB+∠BOC,
∠AOB=∠AOC-∠BOC,
O
C
B
A
教学目标
新课讲解
4.利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
15°
75°
教学目标
新课讲解
165°
一副三角尺上的角都是常用的角,它们是30°,45°,60°,90°的角,利用这些角可以很方便地画出与这些角相关的一些特殊角,如15°,75°,105°,120°,135°,150°,165°等.它们都是15°的倍数.
15°
75°
105°
135°
教学目标
新课讲解
在透明纸上画一个角,沿着顶点对折,使角的两边重合.
我们把射线OB叫做∠AOC的角平分线.
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
A
O
C
B
教学目标
新课讲解
角的三等分线.
OB,OC是∠AOD的三等分线.
教学目标
新课讲解
作角平分线有以下两种方法:
(1)借助量角器画图:以已知角顶点为顶点,已知角的一边为边,在已知线的内部画一个度数等于已知角度数一半的角,则这个角的另一边就是已知角的平分线.
(2)用折叠方法:把角沿顶点对折,使角的两边重合,沿折痕在角的内部画一条射线即为已知角的平分线.
教学目标
新课讲解
例1 如图,O是直线AB上一点,∠AOC=53°17′,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC
=180°- 53 ° 17′
=126°43′.
B
O
C
A
教学目标
新课讲解
例2 把一个周角7等分,每一份是多少度的角(精确到分)?
解:360 ÷7=51 +3 ÷7
=51 +180′÷7
≈51 26′.
答:每份约是51 26′.
巩固练习
1.如图所示,用“=”“>”或“<”填空.
(1)∠AOC ∠AOB+∠BOC;
(2)∠AOC ∠AOB;
(3)∠BOD-∠BOC ∠DOC;
(4)∠AOD ∠AOC+∠BOD.
=
=
>
<
巩固练习
2.如图,将两块直角三角尺的直角顶点C叠放在一起,
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB和∠DCE的大小关系,并说明理由.
E
D
C
B
A
巩固练习
解:(1)∵∠ECB=90°,∠DCE=35°.
∴∠DCB=90°-35°=55°.
∵∠ACD=90°,
∴∠ACB=∠ACD+∠DCB=145°.
(2)∵∠ACB=140°,∠ACD=90°.
∴∠DCB=140°-90°=50°.
∵∠ECB=90°,
∴∠DCE=90°-50°=40°.
E
D
C
B
A
巩固练习
解:(3)猜想∠ACB+∠DCE=180°.
∵∠ECB=90°,∠ACD=90°.
∴∠ACB=∠ACD+∠DCB=90°+∠DCB.
∵∠DCE=∠ECB-∠DCB=90°-∠DCB.
∴∠ACB+∠DCE=180°.
E
D
C
B
A
巩固练习
3.如图所示,OB,OC是∠AOD的任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,则表示∠AOD的代数式是( ).
A.2α-β B.α-β C.α+β D.以上都不正确
N
M
D
C
B
A
O
巩固练习
解析:∵∠MON=α,∠BOC=β,
∴∠MON-∠BOC=∠CON+∠BOM=α-β,
又∵OM平分∠AOB,ON平分∠COD,
∴∠CON=∠DON,∠AOM=∠BOM,
由题意得∠AOD=∠MON+∠DON+∠AOM
=∠MON+∠CON+∠BOM
=α+(α-β)=2α-β.
答案:A.
N
M
D
C
B
A
O
课堂小结
1.谈谈你对角的大小的比较方法的认识.
2.谈谈你对角平分线的认识.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
