4.3.3余角和补角 第一课时(课件)
图片预览





文档简介
(共19张PPT)
余角和补角
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
比萨斜塔建于1173年,工程曾间断了两次很长的时间,历经约二百年才完工.设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜.
你知道比萨斜塔倾斜多少度角吗?它现在与地面成多少度角?
比萨斜塔倾斜了3.97°,它现在与地面成的夹角是86.03°.
教学目标
新课讲解
什么叫互为余角?互余的定义是什么?
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
即:若∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
教学目标
新课讲解
练一练1:图中给出的各角,哪些互为余角?
答:10°和80°互为余角;25°和65°互为余角;
44°和46°互为余角.
80°
46°
65°
44°
25°
10°
教学目标
新课讲解
什么叫做互为补角?
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
即:若∠3+∠4=180°,那么∠3是∠4的补角,∠4也是∠3的补角.
定义中的“互为”是什么意思?
即每一个角都是另一个角的余角(补角).
教学目标
新课讲解
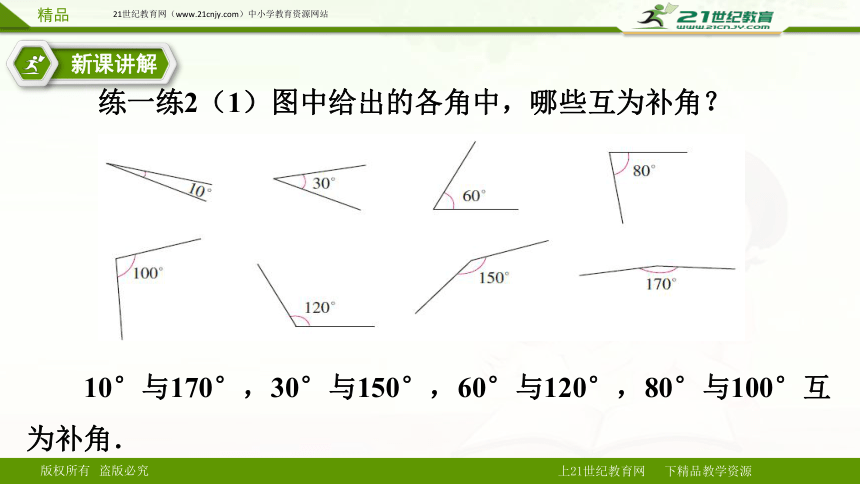
练一练2(1)图中给出的各角中,哪些互为补角?
10°与170°,30°与150°,60°与120°,80°与100°互为补角.
教学目标
新课讲解
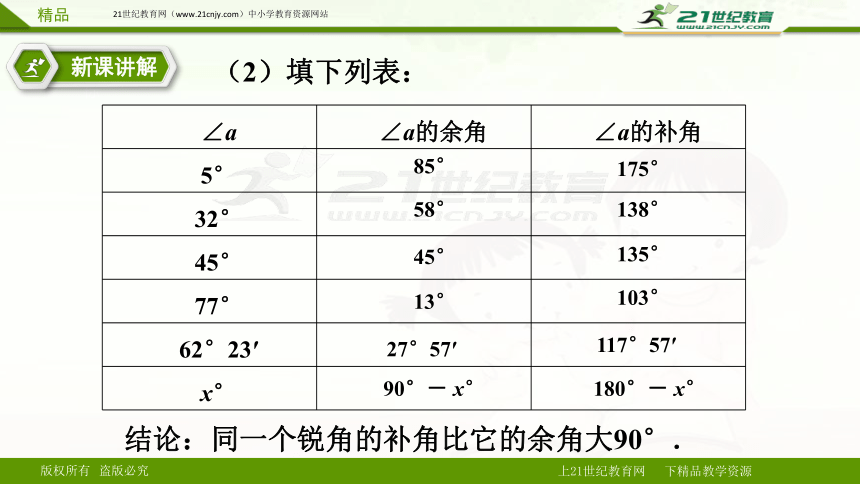
∠a ∠a的余角 ∠a的补角
5°
32°
45°
77°
62°23′
x°
结论:同一个锐角的补角比它的余角大90°.
(2)填下列表:
85°
175°
58°
13°
45°
138°
135°
103°
27°57′
117°57′
90°- x°
180°- x°
教学目标
新课讲解
1
2
3.探究补角的性质:
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
∵ ∠1 +∠2=180°, ∠3 +∠4=180°.
∴ ∠2=180°-∠1 , ∠4=180°- ∠3.
∵ ∠1 =∠3.
∴ 180°-∠1 =180°- ∠3.
即:∠2 =∠4.
3
4
教学目标
新课讲解
4.探究余角的性质:
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
∵ ∠1 +∠2=90°, ∠3 +∠4=90°.
∴ ∠2=90°-∠1 , ∠4=90°- ∠3.
∵ ∠1 =∠3.
∴ 90°-∠1 =90°- ∠3.
即:∠2 =∠4.
1
2
3
4
教学目标
新课讲解
等角(同角)的余角相等.
归纳:
等角(同角)的补角相等.
教学目标
新课讲解
例1 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,图中哪些角互为余角?
重点提醒:(1)(如何表示一个角的余角和补角)∠α的余
角是90°-∠α,∠α的补角是180°-∠α.
(2)互余和互补是两个角的数量关系,与它们的位置无关.
教学目标
新课讲解
所以∠COD +∠COE= ∠AOC+ ∠BOC
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC , ∠BOC,
= (∠AOC+ ∠BOC)
=90°.
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE, ∠AOD和∠COE ,∠COD和∠BOE也互为余角.
巩固练习
1.一个角是70°39′,求它的余角和补角.
解:它的余角是90°-70°39′=19°21′;
它的补角是180°-70°39′=109°21′.
2.一个角的补角是它的3倍,这个角是多少度?
解:由180°-∠α=3∠α,
解得∠α=45°.
3.一个角是钝角,它的一半是什么角?
解:一个角是钝角,它的一半是锐角.
巩固练习
4.如图,E,D,F在同一直线上,∠CDE=90°, ∠1=∠2.
(1)∠ADC与∠BDC有什么关系?为什么?
(2)∠ADF与∠BDE有什么关系?为什么?
2
1
F
E
D
C
B
A
巩固练习
解:(1)∠ADC=∠BDC.
因为∠CDF=∠EDF-∠CDF=180°-90°=90°,
所以∠2+∠BDC=∠CDF=90°.
又因为∠1+∠ADC=∠CDE=90°,且∠1=∠2,
所以∠ADC=∠BDC.
2
1
F
E
D
C
B
A
巩固练习
解:(2)∠ADF=∠BDE.
因为∠ADF=180°-∠1,
∠BDE=180°-∠2,
又因为∠1=∠2,所以∠ADF=∠BDE.
2
1
F
E
D
C
B
A
课堂小结
1.谈谈你对余角和补角的认识.
2.谈谈你对余角和补角性质的理解.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
余角和补角
人教版 七年级上
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
导入新课
比萨斜塔建于1173年,工程曾间断了两次很长的时间,历经约二百年才完工.设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜.
你知道比萨斜塔倾斜多少度角吗?它现在与地面成多少度角?
比萨斜塔倾斜了3.97°,它现在与地面成的夹角是86.03°.
教学目标
新课讲解
什么叫互为余角?互余的定义是什么?
如果两个角的和等于90 (直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
即:若∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
教学目标
新课讲解
练一练1:图中给出的各角,哪些互为余角?
答:10°和80°互为余角;25°和65°互为余角;
44°和46°互为余角.
80°
46°
65°
44°
25°
10°
教学目标
新课讲解
什么叫做互为补角?
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
即:若∠3+∠4=180°,那么∠3是∠4的补角,∠4也是∠3的补角.
定义中的“互为”是什么意思?
即每一个角都是另一个角的余角(补角).
教学目标
新课讲解
练一练2(1)图中给出的各角中,哪些互为补角?
10°与170°,30°与150°,60°与120°,80°与100°互为补角.
教学目标
新课讲解
∠a ∠a的余角 ∠a的补角
5°
32°
45°
77°
62°23′
x°
结论:同一个锐角的补角比它的余角大90°.
(2)填下列表:
85°
175°
58°
13°
45°
138°
135°
103°
27°57′
117°57′
90°- x°
180°- x°
教学目标
新课讲解
1
2
3.探究补角的性质:
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
∵ ∠1 +∠2=180°, ∠3 +∠4=180°.
∴ ∠2=180°-∠1 , ∠4=180°- ∠3.
∵ ∠1 =∠3.
∴ 180°-∠1 =180°- ∠3.
即:∠2 =∠4.
3
4
教学目标
新课讲解
4.探究余角的性质:
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
∵ ∠1 +∠2=90°, ∠3 +∠4=90°.
∴ ∠2=90°-∠1 , ∠4=90°- ∠3.
∵ ∠1 =∠3.
∴ 90°-∠1 =90°- ∠3.
即:∠2 =∠4.
1
2
3
4
教学目标
新课讲解
等角(同角)的余角相等.
归纳:
等角(同角)的补角相等.
教学目标
新课讲解
例1 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,图中哪些角互为余角?
重点提醒:(1)(如何表示一个角的余角和补角)∠α的余
角是90°-∠α,∠α的补角是180°-∠α.
(2)互余和互补是两个角的数量关系,与它们的位置无关.
教学目标
新课讲解
所以∠COD +∠COE= ∠AOC+ ∠BOC
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC , ∠BOC,
= (∠AOC+ ∠BOC)
=90°.
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE, ∠AOD和∠COE ,∠COD和∠BOE也互为余角.
巩固练习
1.一个角是70°39′,求它的余角和补角.
解:它的余角是90°-70°39′=19°21′;
它的补角是180°-70°39′=109°21′.
2.一个角的补角是它的3倍,这个角是多少度?
解:由180°-∠α=3∠α,
解得∠α=45°.
3.一个角是钝角,它的一半是什么角?
解:一个角是钝角,它的一半是锐角.
巩固练习
4.如图,E,D,F在同一直线上,∠CDE=90°, ∠1=∠2.
(1)∠ADC与∠BDC有什么关系?为什么?
(2)∠ADF与∠BDE有什么关系?为什么?
2
1
F
E
D
C
B
A
巩固练习
解:(1)∠ADC=∠BDC.
因为∠CDF=∠EDF-∠CDF=180°-90°=90°,
所以∠2+∠BDC=∠CDF=90°.
又因为∠1+∠ADC=∠CDE=90°,且∠1=∠2,
所以∠ADC=∠BDC.
2
1
F
E
D
C
B
A
巩固练习
解:(2)∠ADF=∠BDE.
因为∠ADF=180°-∠1,
∠BDE=180°-∠2,
又因为∠1=∠2,所以∠ADF=∠BDE.
2
1
F
E
D
C
B
A
课堂小结
1.谈谈你对余角和补角的认识.
2.谈谈你对余角和补角性质的理解.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
