14.1.3 积的乘方 课件
图片预览










文档简介
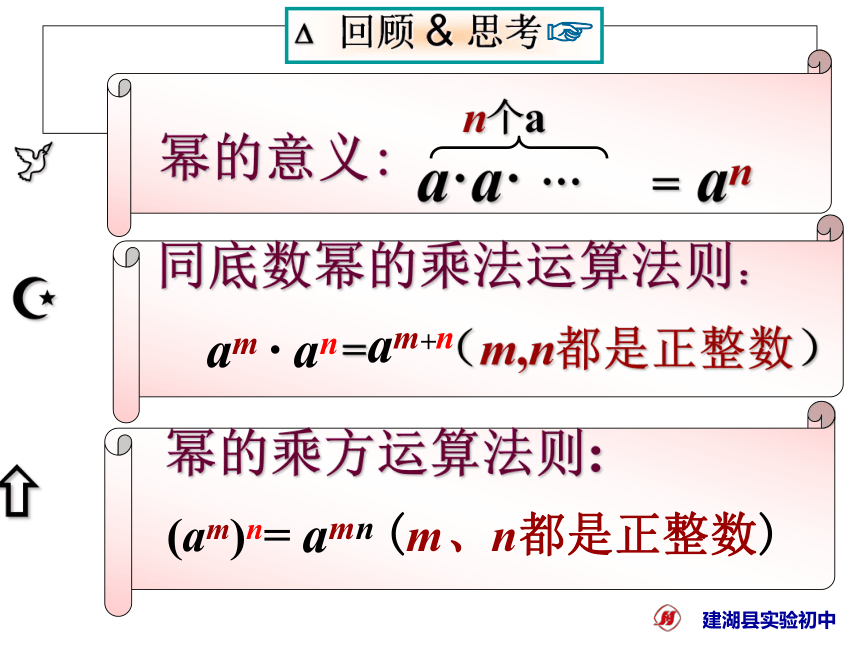
课件31张PPT。14.1.3 积的乘方回顾与思考?幂的意义:an=am+n(m,n都是正整数)(am)n= (m、n都是正整数)amn知识回顾填空:
1. am+am=_____,依据________________.
2. a3·a5=____,依据_______________
________.
3. 若am=8,an=30,则am+n=____.
4. (a4)3=_____,依据___________________.
5. (m4)2+m5·m3=____,(a3)5·(a2)2=____.2am合并同类项法则a8同底数幂乘法的运算性质240a12幂的乘方的运算性质2m8a19同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)(1)(2)⑴ (1×2)4=____; 14×24 =_____;
⑵ [3×(-2)]3=_____; 33×(-2)3=_____;
⑶ ( )2 1616-216-216填空:1(ab)n=_____. (n为正整数)anbn × =× =积的乘方
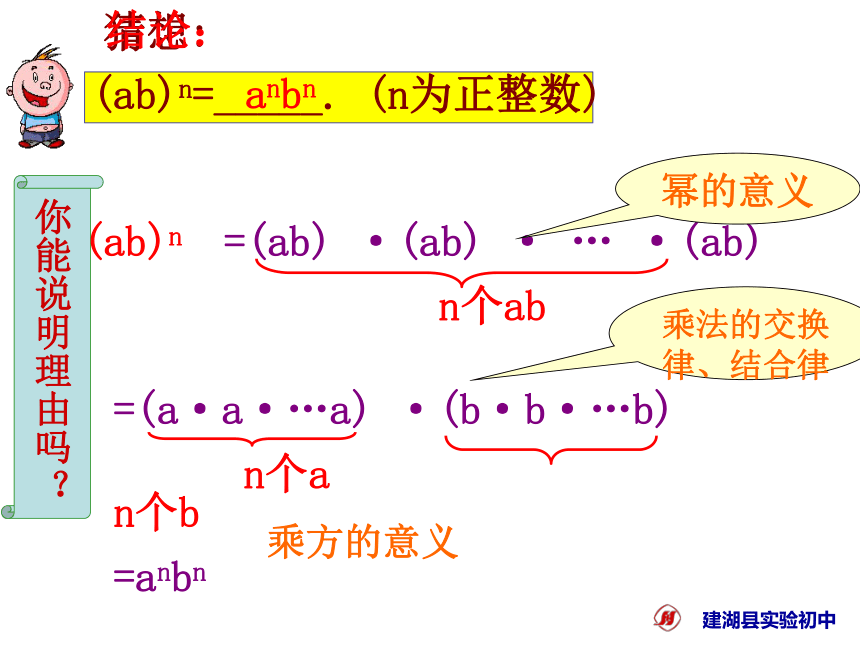
(ab)n =?思考:猜想: (ab)n = (当m、n都是正整数)即:(乘方的意义)(乘法结合律)(乘方的意义)an·bn(ab)n = ab·ab·……·ab=(a·a·……·a) (b·b·……·b)=an·bn (ab)n = (n都是正整数)an·bn 语言叙述:积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(ab)n=_____.(n为正整数)猜想:你能说明理由吗? =(ab) ·(ab) · … ·(ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn(ab)n幂的意义乘法的交换律、结合律乘方的意义(ab)n=_____. (n为正整数)anbn结论:积的乘方的运算性质:结论:(ab)n=_____. (n为正整数)anbn你能用文字语言叙述这个性质吗? 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.(1) (2a)3(2) (-5b)3(3) (xy2)2(4) (-2x3)4例题 计算(2a)3 =23·a3=8a3(-5b)3 =(-5)3·b3=-125b3(xy2)2 =x2· (y2)2=x2y4(-2x3)4 =(-2)4· (x3)4 =16x122、计算:
(1)(-2x2y3)3 答案(2) 81a12b8c4答案 (1) -8x6y9(2) (-3a3b2c)41 计算: a3 ·a4· a+(a2)4+(-2a4)2解:原式=a3+4+1+a2×4+(-2)2 · (a4)2=a8+a8+4a8=6a8试一试:积的乘方的运算性质:(ab)n=_____.(n为正整数)(ab)n=_____. (n为正整数)anbn 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.例1 计算:(5m)3 (2) (-xy2)3
(3)(3×103)21.计算:
(-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3××x342.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4 b4 ( )1( )
( )
( )
( )
( )1.在括号里填写适当的计算依据:(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6积的乘方的运算性质积的乘方的运算性质积的乘方的运算性质幂的乘方的运算性质幂的乘方的运算性质2.计算:
(1) (-3x2y)3 (2) (-5ab)2
(3) (2xnym)2 (4) (-2xy2z3)4
3.计算:
⑴ (-a2)3.(-a3)2
⑵ -(n2).(-n5)3
⑶ a5.a3+(2a2)4
⑷ (-2a)3-(-a).(a)2=1解:原式试一试你会计算吗?
× ×逆用积的乘方的运算性质× × 三、例题例1 计算与化简:
① (2b)5 ②(-xy)4
③(-x2yz3)3 ④ (x-1)2(1-x)3
(积的乘方同样具有可逆性)
思考: (-a)n= -an (n为正整数)对吗?当n为奇数时, (-a)n= -an(n为正整数)
当n为偶数时, (-a)n=an(n为正整数)
(分类的思想)计算: ×
×
×
×
逆用幂的乘方的运算性质幂的乘方的运算性质逆用同底数幂的乘法运算性质逆用积的乘方的运算性质= ●●●
●
●
●
●
●
一起探讨:(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一: (0.04)2004×[(-5)2004]2=1=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2004×[(-5)2004]2 四、典型习题
1、幂的混合运算
eg:a3 ·a4· a+(a2)4+(-2a4)2
注意运算顺序:
积的乘方 幂的乘方同底数幂的乘法练习: 2(x3)2 · x3-(3x3)3+(5x)2 ·x7
2 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除,最后算加减。=2x9-27x9+25x9=02 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除,最后算加减。=2x9-27x9+25x9=0拓展训练
(5)若n是正整数,且 ,
求 的值。本节课你的收获是什么?小结本节课你学到了什么?每个因式分别乘方后的积 小结
1. am+am=_____,依据________________.
2. a3·a5=____,依据_______________
________.
3. 若am=8,an=30,则am+n=____.
4. (a4)3=_____,依据___________________.
5. (m4)2+m5·m3=____,(a3)5·(a2)2=____.2am合并同类项法则a8同底数幂乘法的运算性质240a12幂的乘方的运算性质2m8a19同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则)(1)(2)⑴ (1×2)4=____; 14×24 =_____;
⑵ [3×(-2)]3=_____; 33×(-2)3=_____;
⑶ ( )2 1616-216-216填空:1(ab)n=_____. (n为正整数)anbn × =× =积的乘方
(ab)n =?思考:猜想: (ab)n = (当m、n都是正整数)即:(乘方的意义)(乘法结合律)(乘方的意义)an·bn(ab)n = ab·ab·……·ab=(a·a·……·a) (b·b·……·b)=an·bn (ab)n = (n都是正整数)an·bn 语言叙述:积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(ab)n=_____.(n为正整数)猜想:你能说明理由吗? =(ab) ·(ab) · … ·(ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn(ab)n幂的意义乘法的交换律、结合律乘方的意义(ab)n=_____. (n为正整数)anbn结论:积的乘方的运算性质:结论:(ab)n=_____. (n为正整数)anbn你能用文字语言叙述这个性质吗? 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.(1) (2a)3(2) (-5b)3(3) (xy2)2(4) (-2x3)4例题 计算(2a)3 =23·a3=8a3(-5b)3 =(-5)3·b3=-125b3(xy2)2 =x2· (y2)2=x2y4(-2x3)4 =(-2)4· (x3)4 =16x122、计算:
(1)(-2x2y3)3 答案(2) 81a12b8c4答案 (1) -8x6y9(2) (-3a3b2c)41 计算: a3 ·a4· a+(a2)4+(-2a4)2解:原式=a3+4+1+a2×4+(-2)2 · (a4)2=a8+a8+4a8=6a8试一试:积的乘方的运算性质:(ab)n=_____.(n为正整数)(ab)n=_____. (n为正整数)anbn 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.例1 计算:(5m)3 (2) (-xy2)3
(3)(3×103)21.计算:
(-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3××x342.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4 b4 ( )1( )
( )
( )
( )
( )1.在括号里填写适当的计算依据:(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6积的乘方的运算性质积的乘方的运算性质积的乘方的运算性质幂的乘方的运算性质幂的乘方的运算性质2.计算:
(1) (-3x2y)3 (2) (-5ab)2
(3) (2xnym)2 (4) (-2xy2z3)4
3.计算:
⑴ (-a2)3.(-a3)2
⑵ -(n2).(-n5)3
⑶ a5.a3+(2a2)4
⑷ (-2a)3-(-a).(a)2=1解:原式试一试你会计算吗?
× ×逆用积的乘方的运算性质× × 三、例题例1 计算与化简:
① (2b)5 ②(-xy)4
③(-x2yz3)3 ④ (x-1)2(1-x)3
(积的乘方同样具有可逆性)
思考: (-a)n= -an (n为正整数)对吗?当n为奇数时, (-a)n= -an(n为正整数)
当n为偶数时, (-a)n=an(n为正整数)
(分类的思想)计算: ×
×
×
×
逆用幂的乘方的运算性质幂的乘方的运算性质逆用同底数幂的乘法运算性质逆用积的乘方的运算性质= ●●●
●
●
●
●
●
一起探讨:(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一: (0.04)2004×[(-5)2004]2=1=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2004×[(-5)2004]2 四、典型习题
1、幂的混合运算
eg:a3 ·a4· a+(a2)4+(-2a4)2
注意运算顺序:
积的乘方 幂的乘方同底数幂的乘法练习: 2(x3)2 · x3-(3x3)3+(5x)2 ·x7
2 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除,最后算加减。=2x9-27x9+25x9=02 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7解:原式=2x6 · x3-27x9+25x2 ·x7 注意:运算顺序是先乘方,再乘除,最后算加减。=2x9-27x9+25x9=0拓展训练
(5)若n是正整数,且 ,
求 的值。本节课你的收获是什么?小结本节课你学到了什么?每个因式分别乘方后的积 小结
