14.1.3 积的乘方 课件

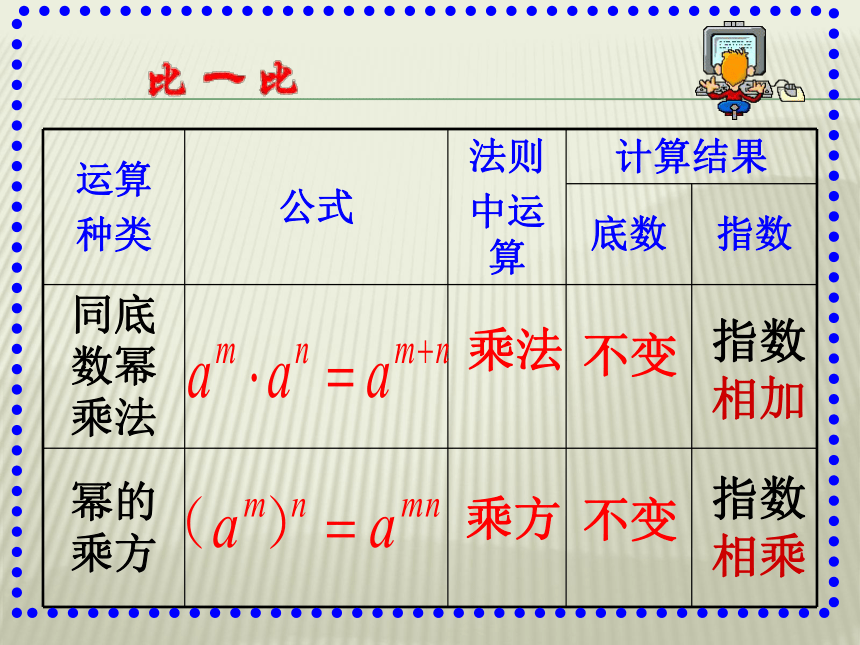
课件21张PPT。乘法乘方不变不变指数
相加指数
相乘14.1.3积的乘方同理：（乘方的意义）（乘法交换律、结合律）（同底数幂相乘的法则）(1)(2)积的乘方
(ab)n =?思考：猜想: (ab)n = (当m、n都是正整数)即:（乘方的意义）（乘法结合律）（乘方的意义）an·bn(ab)n = ab·ab·……·ab=(a·a·……·a) (b·b·……·b)=an·bn (ab)n = (n都是正整数)an·bn 语言叙述：积的乘方,等于把积的每一因式分别乘方,再把所得的幂相乘.(1) (2a)3(2) (-5b)3(3) (xy2)2(4) (-2x3)4例题 计算(2a)3 =23·a3=8a3(-5b)3 =(-5)3·b3=-125b3(xy2)2 =x2· (y2)2=x2y4(-2x3)4 =(-2)4· (x3)4 =16x12公 式 的 拓 展(abc)n=an·bn·cn(abc)n=[(ab)·c]n=(ab)n·cn= an·bn·cn.(-2xy)4=(-2)4x4y4=16x4y4　　　　　　　　×√×××下面的计算对不 对？
如果不对，怎样改正？公式的反向使用(ab)n = an·bn （m,n都是正整数）反向使用:an·bn = (ab)n 试用简便方法计算:(1) 23×53 (2) 28×58 = (2×5)3= 103= (2×5)8= 108(3) (-5)15 × (-2)15 (4) 24 × 44 ×(-0.125)4 = (-5)×[(-5)×(-2)]15= -5×1015 = [2×4×(-0.125)]4= 14= 1 .ＤＤCBA下列选项中正确的是(-2×103)3=(-2)3×(103)3=-8×106知识拓展
（1） a3 .a4.a+(a2)4+(-2a4)2
（2） 2(x3)2.x3－(3x3)3＋(5x)2.x7
注意：运算顺序是先乘方，再乘除，
最后算加减。拓展训练
（5）若n是正整数，且 ，
求 的值。检测三：计算:
（1）(-3x)3
（2） (-5ab)2
(xy2)2
(-2xy3z2)4注意:
（1）负数乘方的符号法则。
（2）积的乘方等于积中“每一个”因式
乘方的积，防止有的因式漏乘方错误。
（3）在计算(-2xy3z2)4=(-2)4x4(y3)4(z2)4
=16x4y12z8的过程中，应把y3 , z2 看
作一个数，再利用积的乘方性质进行
计算。 (1)（ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )堂清:一，判断 2、计算:
(1) (ab)8 (2) (2m)3
(3) (-xy)5 (4) (5ab2)3
(5) (2×102)2
(6) (-3×103)3一起探讨（选做题）：
(0.04)2004×[(-5)2004]2一起探讨：(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一： (0.04)2004×[(-5)2004]2=1=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 说明：逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二： (0.04)2004×[(-5)2004]2思维延伸已知,xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m?x2n; (3) x 3m+2n.解: (1) x m+n=x m?x n= ×3= ;
(2) x2m?x2n=(x m )2?(x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m?x2n=(x m)3?(x n)2=( )3×32
= × 9 = 课堂小结：（1）本节课学习了积的乘方的运算性质
积的乘方等于把积的每一个因式乘方后，再把所得的幂相乘。
（2）学习了一种常见的数学方法：
把某个式子看作一个数或字母。
（3）今后学习中要注意灵活运用积的乘方的
运算性质，注意符号的确定和逆向运用。