14.2.1 平方差公式 课件
图片预览







文档简介
课件28张PPT。14.2.1平方差公式14.2乘法公式(第1课时)有一位庄园主,把一块边长为a米的正方形土地,自己在左下角种植了边长为b米的正方形玉米地后租给张老汉种植。 a 米(a+b)(a-b) = a2-b2
平方差公式 左边
两个数的和乘以这两个数
的差 右边
这两数的平方差。 。即两个二项式中有
两项相等,另两项是互为
相反数。即相等数的平方
减去互为相反数
的数的平方。请注意:
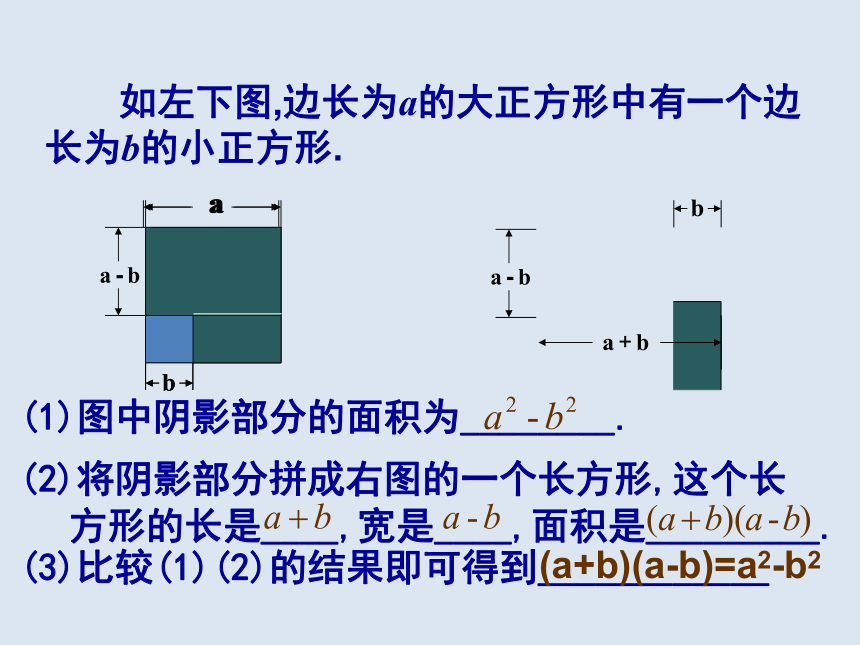
(公式中的a,b既可代表具体的数,还可代表单项式或多项式。)(1+2x)(1-2x)= 12-(2x)2注意加上括号!(1)图中阴影部分的面积为________.(3)比较(1)(2)的结果即可得到____________(a+b)(a-b)=a2-b2 你能根据图中的面积说明平方差公式吗?1、判断下列式子是否可用平方差公式。 考考你 (1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7 )(-4k3+3y2)(-4k3-3y2)
是否是是是是否范例例1、运用平方差公式计算:
(1) (3x+2)(3x-2) (2) (b+2a)(2a-b)
(3)(-x+2y)(-x-2y) 解:(1) (3x+2)(3x-2) =(3x)2-22=9x2-4(2) (b+2a)(2a-b)=(2a)2-b2=(2a+b)(2a-b)=4a2-b2(3) (-x+2y)(-x-2y)=(-x)2-(2y)2=x2-4y2 (1) (3x+2)(3x-2)变式一 ( -3x+2)(-3x-2)变式二 ( -3x-2)(3x-2)变式三 (-3x+2)(3x+2)=(-3x)2-22变一变,你还能做吗? =(-2)2-(3x)2=22-(3x)2请你判断下列计算对不对?为什么?
(x2+2)(x2-2)=x4-2 ( )
(4x-6)(4x+6)=4x2-36 ( )
(2x+3)(x-3)=2x2-9 ( )
(4) (5ab+1)(5ab-1)=25a2b2-1 ( )
(5) (mn-1)(mn+1)=mn2-1 ( )×√×××
(a+b)(a-b)=(a)2-(b)2相反为b 相同为a 适当交换合理加括例2:计算 (1)102×98
(2) (y+2)(y-2)-(y-1)(y+5)
(3)–3x(x+1)(x-1) - x(3x+2)(2-3x)
(3) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x(1)解:原式=(100+2)(100-2)
=1002-22
=10000-4
=9996(2)解:原式=y2-4-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1范例例3:解方程或不等式
(1)(2x+1)(2x-1)+3(x+2)(x-2)=(7x+1)(x-1)
(2)求(x+5)(x+2)-(x+2)(x-2)<28的正整数解解:(1) 4x2-1+3(x2-4)=7x2-6x-1
4x2-1+3x2-12= 7x2-6x-1
6x=12 x=2 (2) x2+7X+10-x2+4 <28
7x +14<28 7x<14 x <2
因为x为正整数,所以不等式的解取1。若(a+b+1)(a+b-1)=63,则a+b=——解:(a+b)2-1=63
(a+b)2=64
a+b=±8思考(a+b+c)(a+b-c)是否可用平方差公式计算?怎样应用公式计算?
(a+b)2 - c2下列多项式相乘,正确的有( )
(1)(a+b-c)(a-b+c)=a2-(b-c)2
(2)(a-b+c)(-a+b-c)=b2-(a+c)2
(3)(a-b+c)a-b-c)=a2-(b-c)2
(4)(a+b-c)(a-b+c)=(b-c)2-a2
A.1 个 B.2 个 C.3 个 D.4个A精心选一选位置变化 符号变化 系数变化 指数变化 增因式变化 增项变化 连用公式变化 逆用公式变化 平方差公式 (a+b)(a-b) = a2-b2
①位置变化 平方差公式 ③系数变化平方差公式 ②符号变化平方差公式 ④指数变化平方差公式 ⑤增因式变化如平方差公式 (x+y)(x-y)(-x-y)(-x+y)=(x2-y2)[ (-x)2-y2 ]
=(x2-y2)(x2-y2)
=x4-2x2y2+y4
⑥增项变化平方差公式 ⑦连用公式变化平方差公式 (x+y)(x-y)(x2+y2)=(x2-y2)(x2+y2)=x4-y41、巧算:99×101× 10001开拓新视野,你会更聪明
2、计算:(2+1)(22+1)(24+1)…(232+1)+1
并确定其个位数字是多少?3、已知:(m+35)2=13302921,求(m+45)(m+25)的值。 2.利用平方差公式计算:
(1)(a+3b)(a - 3b)=
(2)(3+2a)(-3+2a)=
(3)(-2x2-y)(-2x2+y)=
(4)51×49=
(5)(3x+4)(3x-4)-(2x+3)(3x-2)=(a)2-(3b)2 =4 a2-9;=4x4-y2.练习
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2; (2)(-3a-2)(3a-2)=9a2-4.(2a+3)(2a-3)=a2-9b2 ;=(2a)2-32 (-2x2 )2-y2 (50+1)(50-1)=502-12 =2500-1=2499(9x2-16) -(6x2+5x -6)=3x2-5x+10利用平方差公式计算: (1)(5+6x)(5-6x); (2)(x-2y)(x+2y);
(3)(-m+n)(-m-n). 知识应用,加深对平方差公式的理解 下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1+x) ; (2)(a+b)(b-a) ;
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). 1.通过本节课的学习我有哪些收获?
2.通过本节课的学习我有哪些疑惑?
3.通过本节课的学习我有哪些感受?小 结课本P112习题14.2第1题。
平方差公式 左边
两个数的和乘以这两个数
的差 右边
这两数的平方差。 。即两个二项式中有
两项相等,另两项是互为
相反数。即相等数的平方
减去互为相反数
的数的平方。请注意:
(公式中的a,b既可代表具体的数,还可代表单项式或多项式。)(1+2x)(1-2x)= 12-(2x)2注意加上括号!(1)图中阴影部分的面积为________.(3)比较(1)(2)的结果即可得到____________(a+b)(a-b)=a2-b2 你能根据图中的面积说明平方差公式吗?1、判断下列式子是否可用平方差公式。 考考你 (1)(-a+b)(a+b) (2) (-a+b)(a-b)
(3)(a+b)(a-c) (4)(2+a)(a-2)
(5)
(6) (1-x)(-x-1)
(7 )(-4k3+3y2)(-4k3-3y2)
是否是是是是否范例例1、运用平方差公式计算:
(1) (3x+2)(3x-2) (2) (b+2a)(2a-b)
(3)(-x+2y)(-x-2y) 解:(1) (3x+2)(3x-2) =(3x)2-22=9x2-4(2) (b+2a)(2a-b)=(2a)2-b2=(2a+b)(2a-b)=4a2-b2(3) (-x+2y)(-x-2y)=(-x)2-(2y)2=x2-4y2 (1) (3x+2)(3x-2)变式一 ( -3x+2)(-3x-2)变式二 ( -3x-2)(3x-2)变式三 (-3x+2)(3x+2)=(-3x)2-22变一变,你还能做吗? =(-2)2-(3x)2=22-(3x)2请你判断下列计算对不对?为什么?
(x2+2)(x2-2)=x4-2 ( )
(4x-6)(4x+6)=4x2-36 ( )
(2x+3)(x-3)=2x2-9 ( )
(4) (5ab+1)(5ab-1)=25a2b2-1 ( )
(5) (mn-1)(mn+1)=mn2-1 ( )×√×××
(a+b)(a-b)=(a)2-(b)2相反为b 相同为a 适当交换合理加括例2:计算 (1)102×98
(2) (y+2)(y-2)-(y-1)(y+5)
(3)–3x(x+1)(x-1) - x(3x+2)(2-3x)
(3) –3x(x+1)(x-1) - x(3x+2)(2-3x)
= –3x(x2-1) - x(4-9x2)
= –3x3+3x – 4x+9x3
= 6x3-x(1)解:原式=(100+2)(100-2)
=1002-22
=10000-4
=9996(2)解:原式=y2-4-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1范例例3:解方程或不等式
(1)(2x+1)(2x-1)+3(x+2)(x-2)=(7x+1)(x-1)
(2)求(x+5)(x+2)-(x+2)(x-2)<28的正整数解解:(1) 4x2-1+3(x2-4)=7x2-6x-1
4x2-1+3x2-12= 7x2-6x-1
6x=12 x=2 (2) x2+7X+10-x2+4 <28
7x +14<28 7x<14 x <2
因为x为正整数,所以不等式的解取1。若(a+b+1)(a+b-1)=63,则a+b=——解:(a+b)2-1=63
(a+b)2=64
a+b=±8思考(a+b+c)(a+b-c)是否可用平方差公式计算?怎样应用公式计算?
(a+b)2 - c2下列多项式相乘,正确的有( )
(1)(a+b-c)(a-b+c)=a2-(b-c)2
(2)(a-b+c)(-a+b-c)=b2-(a+c)2
(3)(a-b+c)a-b-c)=a2-(b-c)2
(4)(a+b-c)(a-b+c)=(b-c)2-a2
A.1 个 B.2 个 C.3 个 D.4个A精心选一选位置变化 符号变化 系数变化 指数变化 增因式变化 增项变化 连用公式变化 逆用公式变化 平方差公式 (a+b)(a-b) = a2-b2
①位置变化 平方差公式 ③系数变化平方差公式 ②符号变化平方差公式 ④指数变化平方差公式 ⑤增因式变化如平方差公式 (x+y)(x-y)(-x-y)(-x+y)=(x2-y2)[ (-x)2-y2 ]
=(x2-y2)(x2-y2)
=x4-2x2y2+y4
⑥增项变化平方差公式 ⑦连用公式变化平方差公式 (x+y)(x-y)(x2+y2)=(x2-y2)(x2+y2)=x4-y41、巧算:99×101× 10001开拓新视野,你会更聪明
2、计算:(2+1)(22+1)(24+1)…(232+1)+1
并确定其个位数字是多少?3、已知:(m+35)2=13302921,求(m+45)(m+25)的值。 2.利用平方差公式计算:
(1)(a+3b)(a - 3b)=
(2)(3+2a)(-3+2a)=
(3)(-2x2-y)(-2x2+y)=
(4)51×49=
(5)(3x+4)(3x-4)-(2x+3)(3x-2)=(a)2-(3b)2 =4 a2-9;=4x4-y2.练习
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2)=x2-2; (2)(-3a-2)(3a-2)=9a2-4.(2a+3)(2a-3)=a2-9b2 ;=(2a)2-32 (-2x2 )2-y2 (50+1)(50-1)=502-12 =2500-1=2499(9x2-16) -(6x2+5x -6)=3x2-5x+10利用平方差公式计算: (1)(5+6x)(5-6x); (2)(x-2y)(x+2y);
(3)(-m+n)(-m-n). 知识应用,加深对平方差公式的理解 下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1+x) ; (2)(a+b)(b-a) ;
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). 1.通过本节课的学习我有哪些收获?
2.通过本节课的学习我有哪些疑惑?
3.通过本节课的学习我有哪些感受?小 结课本P112习题14.2第1题。
